BÀI 11: TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Khởi động

Câu hỏi: Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của hình tam giác đó. Ba nếp gấp đó có đặc điểm gì?

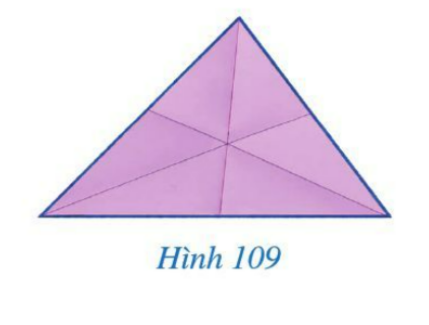
Giải rút gọn:

Đặc điểm: Cùng cắt nhau tại 1 điểm.

I. Đường phân giác của tam giác

Bài 1: Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?

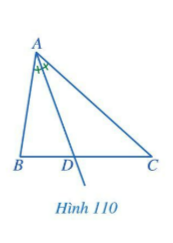
Giải rút gọn:

Đầu mút D là giao điểm của tia phân giác của với BC. 

Đầu mút A là đỉnh của tam giác.

Bài 2: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.

Giải rút gọn:

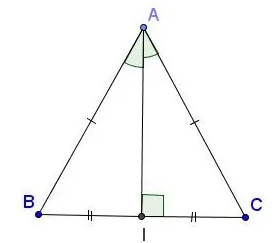
Ta có: △ABC cân tại A => =  

Xét △ABD và △ACD ta có:

= (gt); AB = AC(gt)

= (cmt)

=> △ABD = △ACD (g.c.g)

=> BD = CD (cạnh tương ứng) 

=> AD là trung tuyến của cạnh BC của △ABC (đpcm)

II. Tính chất ba đường phân giác của tam giác

Bài 1: Quan sát các đường phân giác AD, BE, CK của tam giác ABC (hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không?

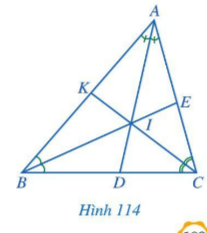
Giải rút gọn:

Ba đường phân giác đó có cùng đi qua một điểm I.

Bài 2: Tìm số đo x trong hình 115

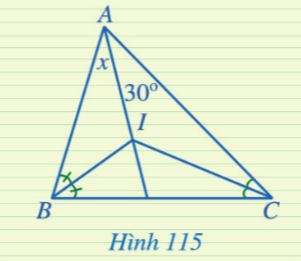
Giải rút gọn:

Xét △ABC có:

BI và CI lần lượt là tia phân giác của và .

BI ∩ CI = I

=> I là giao của 3 đường phân giác trong △ABC => x = = 30⁰

Bài 3: Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Giải rút gọn:

Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.

Trong △ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.

Xét △INC vuông và △IMC vuông:

IC chung; IN = IM.

=> ΔINC = ΔIMC (cạnh huyền – cạnh góc vuông) 

=> = (góc tương ứng).

Tương tự: ΔIPA = ΔINA (ch – cgv) => = (góc tương ứng).

ΔIPB = ΔIMB  (ch – cgv) => = (góc tương ứng).

Xét △IDN và △IDM có:

ID chung; = ; IN = IM.

=> ΔIDN = ΔIDM (c.g.c) ⇒ DN = DM (cạnh tương ứng);

=> = (góc tương ứng)

Mà  + = 180⁰  (2 góc kề bù)

⇒ = = 180⁰ : 2 = 90⁰

=> IC là đường trung trực của cạnh MN.

Tương tự: IA là đường trung trực của PN; IB là đường trung trực của PM.

III. Bài tập

Bài 1: Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.

a. Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?

b. Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?

Giải rút gọn:

a. IMN, INP, IPM là tam giác cân vì có hai cạnh bằng nhau.

b. Xét △INC vuông và △IMC vuông, có:

IC chung; IN = IM.

=> ΔINC = ΔIMC (cạnh huyền – cạnh góc vuông). 

=> CN = CM (cạnh tương ứng).

Vậy △CMN là tam giác cân.

Tương tự: AP = AN; BP = BM.

Vậy △ANP, △BPM, △CMN là tam giác cân.

Bài 2: Cho tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh

Giải rút gọn:

a) I là giao điểm của ba đường phân giác tại ba góc A, B, C 

=> = ; = ; =

Xét △ABC, có:

+ + = 180^∘

ó + + + + + = 180^∘

ó 2 + 2 + 2 = 180^∘

=> + + = 90^∘

b) Xét tam giác BIC:

+ + = 180^∘

ó = 180^∘ − ( +)

Mà   ++ = 90^∘ (cmt) → + = 90^∘ −

=> = 180^∘− (90^∘− ) => = 90^∘ +  

Mà =  (IA là phân giác của ).

Vậy  = 90^∘ + = 90^∘ +

Bài 3: Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC…

Giải rút gọn:

a) Ta có: AB < AC => >  

Mà BI và CI là hai đường phân giác của và => > (đpcm)

b) Ta có: =

Mà > (cmt) => >

Mà IC đối diện với ; IB đối diện với .

=> IC > IB