BÀI 5: TRƯỜNG HỢP BẰNG NHAU THỨ HAI CỦA TAM GIÁC: CẠNH – GÓC – CẠNH

Khởi động

Câu hỏi: Hai chiếc compa ở Hình 45 gợi lên hình ảnh hai tam giác ABC và A'B'C' có: AB = A'B', AC = A'C', =. Hai tam giác ABC và tam giác A'B'C' có bằng nhau hay không?

Giải rút gọn:

ΔABC = ΔA'B'C'.

I. Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c)

Bài 1: Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2cm, ON = 3cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2cm, OQ = 3cm. Chứng minh MQ = NP

Giải rút gọn:

Xét ΔOMQ và ΔOPN, có: 

OM = OP (= 2cm); chung; OQ = ON (= 3cm)

=> ΔOMQ = ΔOPN (c.g.c)

=> MQ = PN (cạnh tương ứng)

Bài 2: Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP=NP

=> MQ = PN (cạnh tương ứng)

Giải rút gọn:

Vì O là tia phân giác của góc xOy

hay  

Xét ΔOMP và ΔONP, ta có: 

OM = ON (gt); (cmt); OP là cạnh chung 

=> ΔOMP = ΔONP (c.g.c)

=> MP = NP (cạnh tương ứng)

II. Áp dụng vào trường hợp bằng nhau hai cạnh góc vuông của tam giác vuông 

III. Bài tập

Bài 1: Chứng minh định lí: "Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn" (trang 74) thông qua việc giải bài tập sau đây: Cho tam giác ABC có AB<AC. Tia phân giác của góc BAC cắt cạnh BC tại điểm D. Điểm E thuộc cạnh AC thỏa mãn AE=AB. Chứng minh:

a. ΔABD = ΔAED

b.

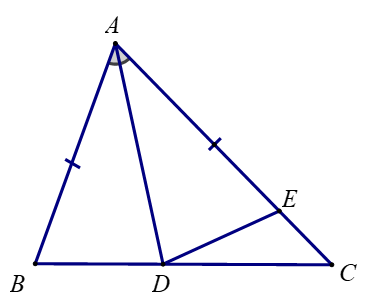
Giải rút gọn:

a. Xét ΔABD và ΔAED có:

AB = AE; ; AD chung

=> ΔABD = ΔAED (c.g.c)

b. Xét ΔABD và ΔAED, có: 

AB = AE (gt); (AD là phân giác góc BAC) 

AD là cạnh chung

=> ΔABD = ΔAED (c.g.c)

=> (góc tương ứng)

Có: (2 góc kề bù) 

Mà: (tổng 3 góc trong tam giác EDC)

=> = => hay  

Bài 2: Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông. Chứng minh:

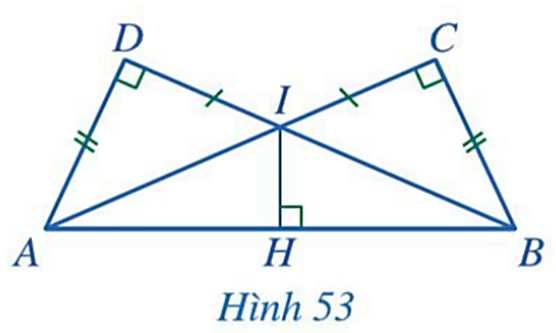
a. IA = IB

b. IH là tia phân giác của góc AIB

Giải rút gọn:

a) Xét ΔADI và ΔICB, có: 

; AD = BC, IC = ID

=> Δ ADI = Δ ICB (c.g.c)

=> IA = IB (cạnh tương ứng)

b) Xét ΔAIH và ΔBIH, ta có: 

IA = IB (cmt); IH chung;  

=> ΔIHA = ΔIHBΔ (cạnh huyền - cạnh góc vuông)

=> (góc tương ứng)

=> IH là tia phân giác của

Bài 3: Có hai xã ở cùng một bên bờ sông Lam. Các kĩ sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã. Để thuận lợi cho người dân đi lại, các kĩ sư cần phải chọn vị trí của cây cầu sao cho tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất. Bạn Nam đề xuất cách xác định vị trí của cây cầu như sau: 

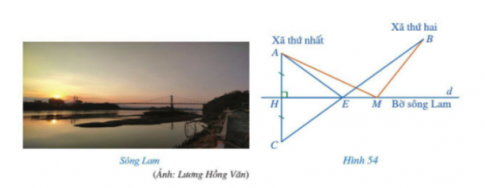
- Kí hiệu điểm A chỉ vị trí xã thứ nhất, điểm B chỉ vị trí xã thứ hai, đường thẳng d chỉ vị trí bờ sông Lam. 

- Kẻ AH vuông góc với d (H thuộc d), kéo dài AH về phía H và lấy điểm C sao cho AH = HC. - Nối C và B, CB cắt đường thẳng d tại điểm E. Khi đó, E là vị trí của cây cầu. Bạn Nam nói rằng: Lấy một điểm M trên đường thẳng d, M khác E thì MA + MB > EA + EB. Em hãy cho biết bạn Nam nói đúng hay sai? Vì sao?

Giải rút gọn: 

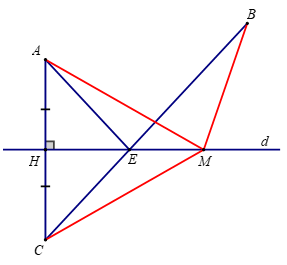
Xét ΔAHE và ΔCHE, có: 

AH = CH (gt); HE là cạnh chung;  

=> ΔAHE = ΔCHE (c.g.c)

=> AE = CE (cạnh tương ứng)

=> AE + EB = CE + EB = CB 

Xét ΔAHM và ΔCHM, có: 

AH = CH (gt); HM là cạnh chung;  

=> ΔAHM = ΔCHM (c.g.c)

=> AM = CM (cạnh tương ứng)

=> AM + MB = CM + MB 

Xét ΔBCM có: CM + MB > CB (hệ thức lượng trong tam giác) 

Hay MA + MB > EA + EB

=> Bạn Nam nói đúng. 

Bài 4: Cho ΔABC = ΔMNP. Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh:

a) AD = MQ;                                                                   

b) DE = QR.

Giải rút gọn: 

Xét ΔABD và ΔMNQ, có:

AB = MQ (do ΔABC = ΔMNP); ; BD = NQ (BC = NP)

=> ΔABD = ΔMNQ (c.g.c)

=> BC = NP (cạnh tương ứng)

b) Ta có ΔABC = ΔMNP (gt)

=> BC = NP (cạnh tương ứng) => BC = NP hay DC = QP

=> AC = MP (cạnh tương ứng) => AC = MP hay EC = RP

Xét ΔDEC và ΔQRP, có:

DC = QP ; (ΔABC = ΔMNP); EC = RP 

=> ΔDEC = ΔQRP (c.g.c) => DE = QR (cạnh tương ứng)