BÀI 9: ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG

Khởi động

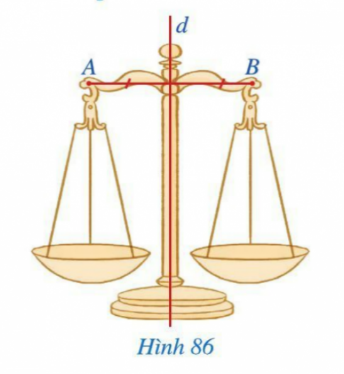
Câu hỏi: Hình 86 minh họa chiếc cân thăng bằng và gợi nên hình ảnh đoạn thẳng AB, đường thẳng d. Đường thẳng d có mối liên hệ gì với đoạn thẳng AB?

Giải rút gọn:

d là đường trung trực của AB.

I. Định nghĩa

Bài 1: Quan sát Hình 87:

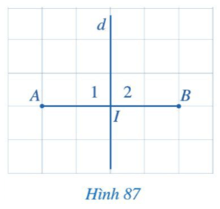
a. So sánh hai đoạn thẳng IA và IB

b. Tìm số đo của các góc I₁=I₂

Giải rút gọn:

a) IA = IB.

b) d ⊥ AB => .

Bài 2: Cho tam giác ABC và M là trung điểm của BC. Biết . Chứng minh AM là đường trung trực của đoạn thẳng BC

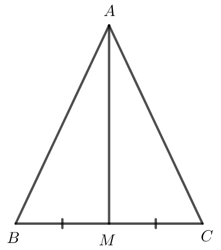
Giải rút gọn:

Ta có: mà (hai góc kề bù).

=> hay AM ⊥ BC.

Ta có: AM ⊥ BC (cmt) mà M là trung điểm của BC 

=> AM là đường trung trực của BC.

II. Tính chất

Bài 1: Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d, M khác O (Hình 90). Chứng minh rằng:

a. ΔMOA=ΔMOB

b. MA = MB

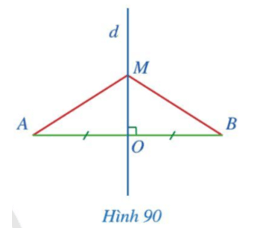
Giải rút gọn:

a) Xét ∆MOA và ∆MOB có:

MO chung; ; OA = OB (gt).

=> ∆MOA = ∆MOB (2 cạnh góc vuông).

b) ∆MOA = ∆MOB (cmt) => MA = MB (cạnh tương ứng).

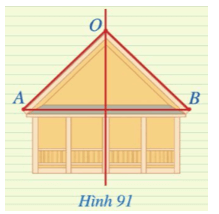
Bài 2: Hình 91 mô tả mặt cắt đứng của một ngôi nhà với hai mái là OA và OB, mái nhà bên trái dài 3m. Tính chiều dài mái nhà bên phải biết rằng điểm O thuộc đường trung trực của đoạn thẳng AB.

Giải rút gọn:

Do O thuộc đường trung trực của đoạn thẳng AB => OA = OB = 3 m.

Vậy chiều dài mái nhà bên phải là 3 m.

Bài 3: Cho đoạn thẳng AB có trung điểm O. Giả sử M là một điểm khác O sao cho MA = MB.

a. Hai tam giác MOA và MOB có bằng nhau hay không? Vì sao?

b. Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?

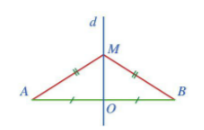
Giải rút gọn:

a) Xét ∆MOA và ∆MOB có:

MO chung; OA = OB (gt); MA = MB (gt).

=> ∆MOA = ∆MOB (c - c - c).

b) Do ∆MOA = ∆MOB (c - c - c) 

=> OA = OB (cạnh tương ứng) và (góc tương ứng).

Ta có: +) OA = OB => O là trung điểm của AB.

+) mà =>

=> MO ⊥ AB.

Khi đó MO ⊥AB tại trung điểm O của AB.

Vậy MO là đường trung trực của đoạn thẳng AB.

Bài 4: Cho tam giác ABC cân tại A.

a. Điểm A có thuộc đường trung trực của đoạn thẳng BC hay không? Vì sao?

b. Đường thẳng qua A vuông góc với BC cắt canh BC tại H. Đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không? Vì sao?

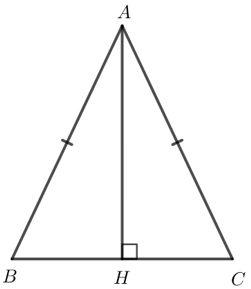
Giải rút gọn:

a) △ABC cân tại A => AB = AC.

=> A thuộc đường trung trực của đoạn thẳng BC.

b) Xét ∆AHB và ∆AHC có:

AB = AC (cmt); ; AH chung.

=> ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông).

=> HB = HC (cạnh tương ứng).

=> H là trung điểm của BC.

Ta có AH ⊥ BC tại trung điểm H 

=> AH là đường trung trực của đoạn thẳng BC.

III. Vẽ đường trung trực của một đoạn thẳng

IV. Bài tập

Bài 1: Trong hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh

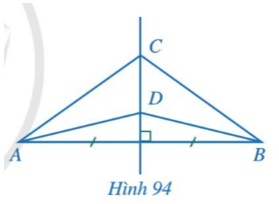
Giải rút gọn:

+ Gọi H là giao điểm của CD và AB.

+ CA = CB (C thuộc đường trung trực của đoạn thẳng AB)

+ DA = DB (D thuộc đường trung trực của đoạn thẳng AB)

Xét ∆CHA và ∆CHB đều vuông tại H có:

CH chung; CA = CB (cmt).

=> ∆CHA = ∆CHB (cạnh huyền - cạnh góc vuông).

=> (góc tương ứng) 

Xét ∆DHA và ∆DHB đều vuông tại H có:

DH chung; DA = DB (cmt).

=> ∆DHA = ∆DHB (cạnh huyền - cạnh góc vuông).

=> (góc tương ứng) 

=> hay .

Bài 2: Trong hình 95 đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD. Chứng minh:

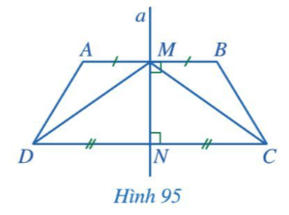
a. AB // CD

b. ΔMNC = ΔMND

c.

d. AD=BC, .

e.  

Giải rút gọn:

a) Ta có: a ⊥ AB và a ⊥ CD. (a là đường trung trực của AB và CD)

=> AB // CD.

b) Xét ∆MNC và ∆MND đều vuông tại N có:

MN chung; NC = ND (gt).

=> ∆MNC = ∆MND (2 cạnh góc vuông).

c) Do ∆MNC = ∆MND (cmt) nên (góc tương ứng).

Do AM // DN nên (2 góc so le trong).

Do BM // CN nên (2 góc so le trong).

=>

d) Do ∆MNC = ∆MND (2 cạnh góc vuông) nên MC = MD (2 cạnh tương ứng).

+ Xét ∆AMD và ∆BMC có:

AM = BM (gt); (cmt); MD = MC (cmt).

=> ∆AMD = ∆BMC (c - g - c).

=> AD = BC (cạnh tương ứng) và (góc tương ứng).

e) Do ∆AMD = ∆BMC (cmt) => (góc tương ứng).

Mà  

=> hay .

Bài 3: Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC. Chứng minh rằng a//b

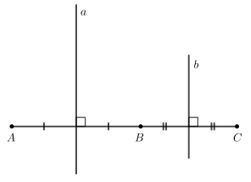
Giải rút gọn:

+) a là đường trung trực của đoạn thẳng AB => a ⊥ AB tại trung điểm của AB.

+) b là đường trung trực của đoạn thẳng BC => b ⊥ BC tại trung điểm của BC.

Mà A, B, C thẳng hàng => a // b.

Bài 4: Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh: 

a. MB = AI + IM

b. MA < MB

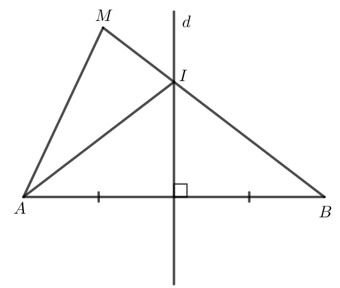
Giải rút gọn:

a) Đường thẳng d cắt MB tại I nên I thuộc đường trung trực của đoạn thẳng AB.

Do đó AI = BI.

Khi đó MB = BI + IM = AI + IM.

b) Xét △AIM có AI + IM > MA.

Mà AI + IM = MB nên MB > MA.