I. ĐỊNH NGHĨA

HĐ1:

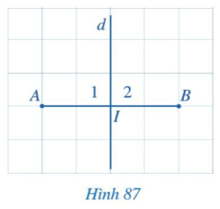
a) Ta thấy IA = IB.

b) Ta thấy d ⊥ AB nên $I_{1}$ = 90°, $I_{2}$ = 90°.

Kết luận: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng ấy.

Ví dụ:

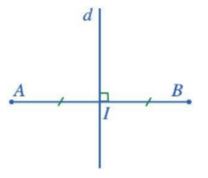
• Đoạn thẳng AB; trung điểm I của đoạn thẳng AB;
• Đường thẳng d vuông góc với AB tại I.

Vì thế, đường thẳng d là đường trung trực của đoạn thẳng AB.

Ví dụ 1 (SGK -tr100)

LT1:

Vì $\widehat{AMB} = \widehat{AMC}$ theo giả thiết

mà $\widehat{AMB} + \widehat{AMC} = 180^{0}$

=> $\widehat{AMB} = \widehat{AMC} = 90^{0}$ hay AM ⊥ BC (1)

Có M là trung điểm của BC (2)

Từ (1) và (2) => AM là đường trung trực của BC

II. TÍNH CHẤT 

HĐ2:

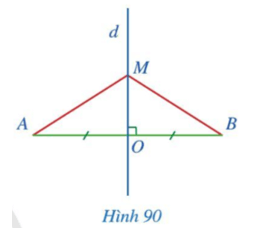
a) Xét ∆MOA vuông tại O và ∆MOB vuông tại O có:

MO chung.

OA = OB (theo giả thiết).

Do đó ∆MOA = ∆MOB (2 cạnh góc vuông).

b) Do ∆MOA = ∆MOB (2 cạnh góc vuông) nên MA = MB (2 cạnh tương ứng).

Kết luận: Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Ví dụ:

Gọi d là đường trung trực của đoạn thẳng AB. Lấy điểm M trên đường thẳng d. Ta có MA = MB.

Ví dụ 2 (SGK -tr101)

LT2:

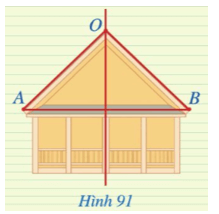
Do O thuộc đường trung trực của đoạn thẳng AB nên OA = OB = 3 m.

Vậy chiều dài mái nhà bên phải là 3 m.

HĐ3:

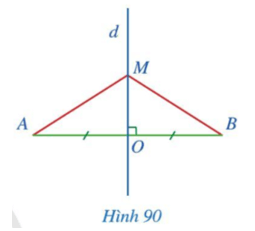
a) Xét ∆MOA và ∆MOB có:

MO chung.

OA = OB (theo giả thiết).

MA = MB (theo giả thiết).

Do đó ∆MOA = ∆MOB (c - c - c).

b) Do ∆MOA = ∆MOB (c - c - c) nên OA = OB (2 cạnh tương ứng) và $\widehat{MOA} = \widehat{MOB}$ (2 góc tương ứng).

Do OA = OB và O nằm giữa A và B nên O là trung điểm của AB.

Do $\widehat{MOA} = \widehat{MOB}$ mà $\widehat{MOA} + \widehat{MOB}$ = 180° nên $\widehat{MOA} = \widehat{MOB} = 90^{0}$

Do đó MO ⊥ AB.

Khi đó MO vuông góc với AB tại trung điểm O của AB.

Vậy MO là đường trung trực của đoạn thẳng AB.

Kết luận: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Ví dụ:

Gọi d là đường trung trực của đoạn thẳng AB, M là điểm sao cho MA = MB. Ta có M nằm trên đường trung trực d của đoạn thẳng AB.

Ví dụ 3 (SGK -tr102)

LT3:

a) Tam giác ABC cân tại A nên AB = AC.

Do AB = AC nên A thuộc đường trung trực của đoạn thẳng BC.

b) Xét ∆AHB vuông tại H và ∆AHC vuông tại H có:

AB = AC (chứng minh trên).

AH chung.

Do đó ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông).

Suy ra HB = HC (2 cạnh tương ứng).

Mà H nằm giữa B và C nên H là trung điểm của BC.

Ta có AH vuông góc với BC tại trung điểm H của BC nên AH là đường trung trực của đoạn thẳng BC.

III. VẼ ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG 

HĐ4:

Vẽ đường trung trực của đoạn thẳng AB = 3cm.

• Bước 1. Vẽ đoạn thẳng AB = 3 cm.

• Bước 2. Vẽ một phần đường tròn tâm A bán kính 2 cm

• Bước 3. Vẽ một phần đường tròn tâm B bán kính 2 cm, cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm C và D.

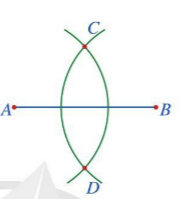
• Bước 4. Vẽ đường thẳng đi qua hai điểm C và D. Đường thẳng CD là đường trung trực của đoạn thẳng AB.