Câu 1: Cho ∆ABC vuông tại A có AB < AC, kẻ đường phân giác BD của góc ABC, (D ∈ AC). Kẻ DM vuông góc với BC tại M. Khẳng định nào dưới đây sai?

• A. DB là tia phân giác góc ADM;
• B. BD là đường trung trực của AM;.

• C. AB = AM;

• D. DA = DM

Câu 2: Cho ba điểm phân biệt H, I, K thẳng hàng, điểm I nằm giữa H và K. Gọi m và n lần lượt là đường trung trực của HI và IK. Khẳng định đúng là

• A. m ⊥ n;

• B. m // n;

• C. m và n trùng nhau;
• D. Cả A, B và C đều sai.

Câu 3: Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt AB tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I

• A. IH = IK

• B. IH = IL
• C. H + IK = IL
• D. IK = IL

Câu 4:  Cho ∆DEF cân tại D. Lấy điểm K nằm trong ∆DEF sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc DF (Q ∈ DF). Điểm K không thuộc đường trung trực của đoạn thẳng:

• A. PQ;

• B. PE;

• C. EF;
• D. DF.

Câu 5: Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là

• A. Chu vi ∆AFB nhỏ hơn chu vi ∆AMB;

• B. Chu vi ∆AFB lớn hơn chu vi ∆AMB;
• C. Chu vi ∆AFB bằng chu vi ∆AMB;
• D. Không đủ dữ kiện để so sánh.

Câu 6: Cho hai điểm A, B nằm trên đường trung trực của đoạn thẳng CD. Gọi M là trung điểm CD. Khẳng định nào sau đây đúng nhất?

• A. ∆ACD cân
• B. ∆BCD cân
• C. Cả A, B đều sai

• D. Cả A, B đều đúng.

Câu 7: Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là

• A. AH ⊥ BC;
• B. AH là đường trung trực của đoạn thẳng BC;
• C. HB = HC;

• D. HA = HB.

Câu 8: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là

• A. ∆AMO = ∆BNO;
• B. ∆AMN cân tại A;

• C. ∆AMB cân tại A;

• D. ∆ANB cân tại N.

Câu 9: Cho hình vẽ dưới đây.

Khẳng định đúng là

• A. h là đường trung trực của đoạn thẳng MN;

• B. b là đường trung trực của đoạn thẳng AB;
• C. d là đường trung trực của đoạn thẳng EF;
• D. f là đường trung trực của đoạn thẳng IJ.

Câu 10: Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”

• A. Thuộc;
• B. Nằm trên;

• C. Cách đều;

• D. Nằm trong.

Câu 11: Cho hình vẽ, biết AC = 8 cm và chu vi ∆ABC bằng 24 cm.

Độ dài cạnh BC là

• A. 4 cm;
• B. 6 cm;

• C. 8 cm;

• D. 10 cm.

Câu 12: Cho d à đường trung trực của đonạ thẳng AB. Gọi O là trung điểm AB. Trên d lấy hai điểm M, N sao cho Om = On. Tứ giác AMBN là hình gì ?

• A. Hình chữ nhật
• B. Hình vuông

• C. Hình thoi

• D. Hình bình hành

Câu 13: Cho ∆MNP vuông tại M có $\widehat{P}$ = 50°. Trên tia đối của tia MP, lấy điểm Q sao cho MQ = MP. Tính số đo $\widehat{QNP}$.

• A. 30°;
• B. 120°;
• C. 60°;

• D. 80°.

Câu 14: Cho $\widehat{xOy}$ =60°. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Lấy điểm C sao cho OB là đường trung trực của AC. Gọi I là giao điểm của AC và Oy. Chọn khẳng định sai.

• A. ∆BIC = ∆BIA;

• B. $\widehat{AOC}$ =80°;

• C. $\widehat{OCA}$=30°;
• D. ∆ABC cân tại B.

Câu 15: Cho tam giác ΔMNP cân tại M, có $\widehat{NMP}=40°$, đường trung trực của MN tại trung điểm K của MN cắt NP tại Q. Tính số đo góc $\widehat{PMQ}$

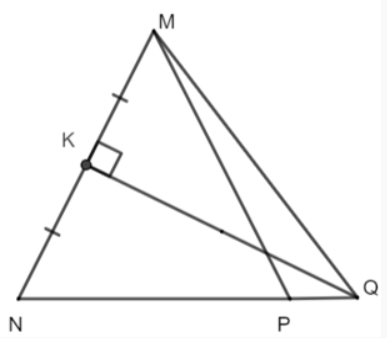
• A. 45°;

• B. 30°;

• C. 50°;
• D. 60°.

Câu 16: Cho tam giác ABC có AH là đường trung trực của BC và H nằm trên đoạn thẳng BC. Tính số đo góc ABC biết số đo góc $\widehat{HAC}$ = 40°.

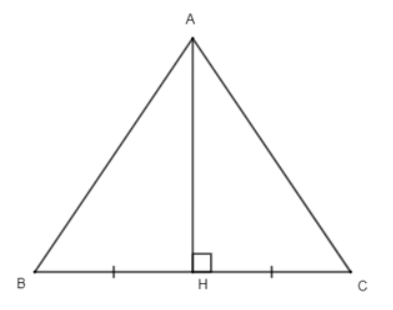
• A. 60°;
• B. 30°;
• C. 40°;

• D. 50°.

Câu 17: Cho ∆ABC vuông tại A có $\widehat{C}$= 40°. Trên tia đối của tia AC lấy điểm D sao cho AC = AD. ∆BCD là tam giác gì?

• A. Tam giác vuông;
• B. Tam giác vuông cân;

• C. Tam giác cân;

• D. Tam giác đều.

Câu 18: Hình vẽ bên dưới được tạo bởi một đường trung trực qua một đoạn thẳng. Độ dài cạnh BD là:

• A. BD = 6 cm;
• B. BD = 7 cm;
• C. BD = 5 cm;

• D. BD = 8 cm.

Câu 19: Cho tam giác MNP có MP = 9 cm, NP = 16 cm. Vẽ đường trung trực của MN cắt NP tại K. Chu vi tam giác KMP là

• A. 7 cm;

• B. 25 cm;

• C. 34 cm;
• D. 41 cm.

Câu 20: Cho tam giác ABC đều cạnh 20 cm. Trên AB lấy D sao cho AD = 8 cm. Đường trung trực của AD cắt AC tại D. Chu vi tứ giác BCFD là

• A. 60 cm;
• B. 40 cm;

• C. 52 cm;

• D. 42 cm.