BÀI 7: TAM GIÁC CÂN

Khởi động

Câu hỏi: Hai thanh giằng của cầu Long Biên bắc qua sông Hồng ở Thủ đô Hà Nội (hình 68) gợi nên hình ảnh tam giác ABC có sự đối xứng và cân bằng. Tam giác ABC như vậy gọi là tam giác gì?

Giải rút gọn:

ΔABC là tam giác cân.

I. Định nghĩa

Bài 1: Trong hình 69, hai cạnh AB và AC của tam giác ABC có bằng nhau hay không?

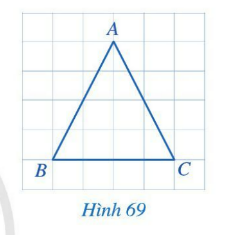
Giải rút gọn:

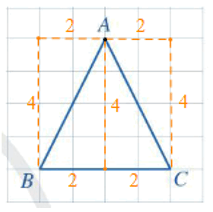
AB = AC.

II. Tính chất

Bài 1: Cho tam giác ABC cân tại A, tia phân giác của góc A cắt cạnh BC tại D (hình 72)

a. Hai tam giác ABD và ACD có bằng nhau hay không? Vì sao?

b. Hai góc B và C có bằng nhau hay không? Vì sao?

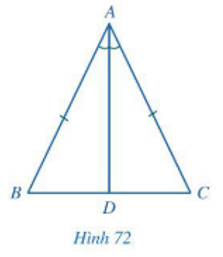
Giải rút gọn:

a) Ta có: AB = AC (ΔABC cân tại A); (AD là tia phân giác góc )

Xét và có:

AB = AC (cmt); (cmt); AD chung.

=>

b) Do nên (góc tương ứng)

III. Dấu hiệu nhận biết

Bài 1: Cho tam giác ABC thỏa mãn . Kẻ AH vuông góc với BC, H thuộc BC (hình 74)

a. Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?

b. Hai cạnh AB và AC có bằng nhau hay không? Vì sao?

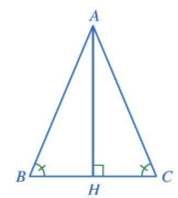
Giải rút gọn:

Do AH BC nên ΔAHB và taΔAHC là hai tam giác vuông tại H.

Xét vuông tại H có: 

=>

Xét vuông tại H có: 

=>

Mà (gt) => .

Xét và có:

; (chứng minh trên).

AH chung

=> (góc nhọn – cạnh góc vuông).

b) Do nên AB = AC (cạnh tương ứng)

Bài 2: Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC cắt AC tại N. Chứng minh tam giác AMN cân.

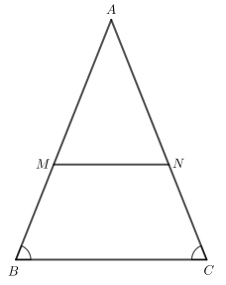
Giải rút gọn:

Ta có: 

+) △ABC cân tại A => .

+) MN // BC => (2 góc đồng vị) và .

Mà =>

Xét △AMN có:  

=> △AMN cân tại A.

IV. Vẽ tam giác cân

V. Bài tập

Bài 1: Cho tam giác ABC cân tại A có M là trung điểm của cạnh AC và N là trung điểm của cạnh AB. Chứng minh BM = CN

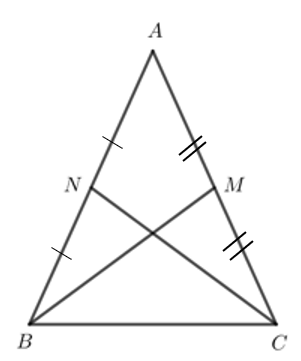
Giải rút gọn:

Ta có:

+) △ABC cân tại A => AB = AC.

+) ; (M, N lần lượt là trung điểm của AC, AB)

Mà AB = AC => AM = AN.

+ Xét và có:

AM = AN (cmt); AB = AC (cmt)

chung.

=> = (c - g - c).

=> BM = CN (cạnh tương ứng).

Bài 2: Cho tam giác ABC có =120^∘.Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.

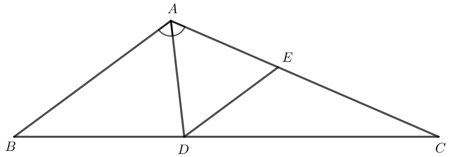
Giải rút gọn:

+ Do AD là tia phân giác của nên .

Do DE // AB nên (2 góc so le trong).

=> .

+ Xét có: 

=> => △ADE đều.

Bài 3: Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm cạnh huyền BC. Chứng minh tam giác MAB vuông cân.

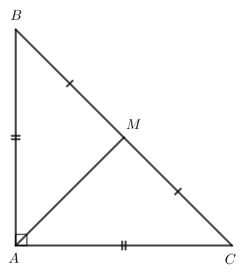
Giải rút gọn:

+ Xét ∆AMB và ∆AMC có:

AM chung; BM = CM (M là trung điểm của BC)

AB = AC (tam giác ABC cân tại A).

=> ∆AMB = ∆AMC (c - c - c).

=> (góc tương ứng).

Mà nên .

△ABC vuông cân tại A 

=> và .

 .

Xét △MAB có:

nên △MAB cân tại M 

=>  

=> AM ⊥ BM hay △MAB vuông tại M 

=> △MAB vuông cân tại M.

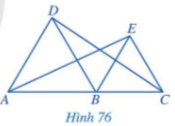
Bài 4: Trong hình 76, cho biết các tam giác ABD và BCE là các tam giác đều. A, B, C thẳng hàng. Chứng minh rằng:

a. AD//BE và BD//CE

b. = = 120⁰

c. AE = CD

Giải rút gọn:

a) △ABD đều => AB = BD = DA và .

△BCE đều => BC = CE = EB và .

Ta có , mà 2 góc này ở vị trí đồng vị.

=> AD // BE.

, mà 2 góc này ở vị trí đồng vị.

=> BD // CE.

b) là góc ngoài tại đỉnh B của ∆ABD 

=>

⇒

c) Xét ∆DBC và ∆ABE có:

DB = AB (cmt); ; BC = BE (cmt).

=> ∆DBC = ∆ABE(c - g - c).

=> CD = EA (cạnh tương ứng).

Bài 5: Trong thiết kế của một ngôi nhà, độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 77 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A.

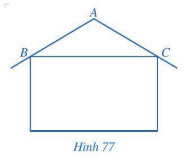
Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:

a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói;

b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng;

c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn.

Giải rút gọn:

△ABC cân tại A nên

Xét △ABC: 

=>

a) Khi thì

Vậy khi 120° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là 30°.

b) thì

Vậy khi 140° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là 20°.

c) thì

Vậy khi 148° thì độ nghiêng của mái nhà so với mặt phẳng nằm ngang là 16°.