I. ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

HĐ1:

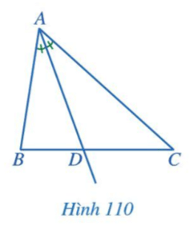
A là đỉnh của tam giác ABC, D là giao điểm của đường phân giác của góc A và cạnh BC.

Kết luận: Trong tam giác ABC tia phân giác của góc A cắt cạnh BC tại điểm D. Khi đó, đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

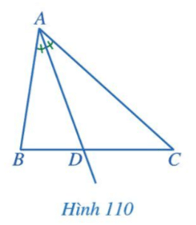
Chú ý: Đôi khi đường thẳng AD cũng được gọi là đường phân giác của tam giác ABC.

Ví dụ 1 (SGK -tr108)

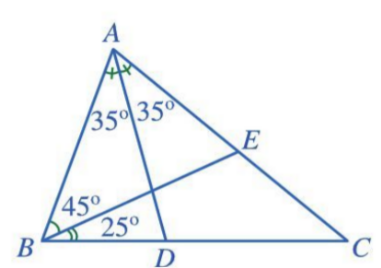
• Đoạn thẳng AD là đường phân giác của tam giác ABC.
• Đoạn thẳng BE không là đường phân giác của tam giác ABC.

Ví dụ 2 (SGK – tr108)

LT1:

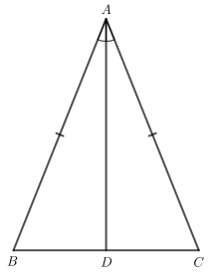
Do tam giác ABC cân tại A nên AB = AC.

Do AD là đường phân giác của ∆ABC nên $\widehat{BAD}=\widehat{CAD}$.

Xét ∆ABD và ∆ACD có:

AB = AC (chứng minh trên).

$\widehat{BAD}=\widehat{CAD}$

AD chung.

Do đó ∆ABD = ∆ACD (c - g - c).

Suy ra BD = CD (2 cạnh tương ứng).

Mà D nằm giữa B và C nên D là trung điểm của BC hay AD là đường trung tuyến của ∆ABC.

Ví dụ 3 (SGK -tr109)

Ta vẽ đường phân giác AD của tam giác ABC như sau:

• Bước 1. Bằng thước thẳng và compa vē tia phân giác Ax của góc $\widehat{BAC}$ 
• Bước 2. Vẽ D là giao điểm của tia Ax với cạnh BC.

Ta vẽ các đường phân giác xuất phát từ đỉnh B và đỉnh C của tam giác ABC bằng cách tương tự.

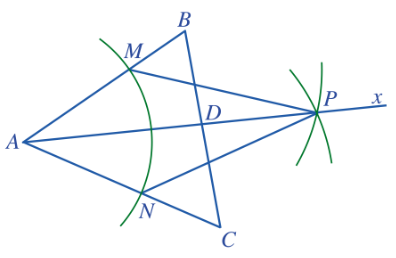
Nhận xét: Mỗi tam giác có ba đường phân giác.

II. TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

HĐ2:

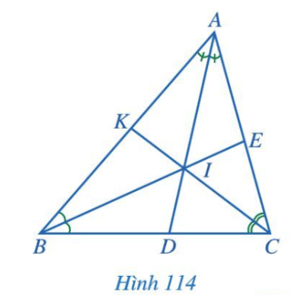
Ta thấy ba đường phân giác AD, BE, CK của tam giác ABC cùng đi qua điểm I.

Định lí: Ba đường phân giác của một tam giác cùng đi qua một điểm

Nhận xét: Để xác định giao điểm ba đường phân giác của một tam giác, ta chỉ cần vẽ hai đường phân giác bất kì và xác định giao điểm của hai đường đó.

Ví dụ 4 (SGK -tr110)

LT2:

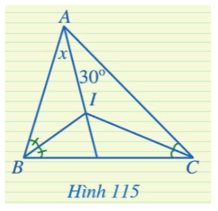
Ta thấy đường phân giác của góc B và góc C cắt nhau tại I nên I là giao điểm ba đường phân giác của tam giác ABC.

Do đó AI là đường phân giác của $\widehat{BAC}$.

$\Rightarrow \widehat{BAI}=\widehat{IAC}\Rightarrow x=30^{o}$

HĐ3:

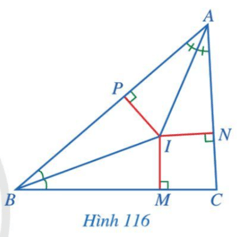
IP = IM = IN.

Nhận xét: Giao điểm ba đường phân giác của một tam giác cách đều ba cạnh của tam giác đó.

Kết luận: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.

Chứng minh: Vẽ các đường phân giác của các góc BAC và CBA cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hinh 117).

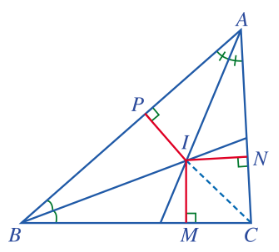
Vì I nằm trên tia phân giác của góc BAC nên IN = IP. Tương tự ta có IP = IM.

Suy ra IM = IN. Do đó điểm I nằm trên đường phân giác của góc ACB.

Vậy ba đường phân giác của tam giác ABC cùng đi qua điểm I.

Mặt khác, ta có: IM = IN = IP. Vậy điểm I cách đều ba cạnh của tam giác ABC.

Ví dụ 5 (SGK -tr110)

LT3:

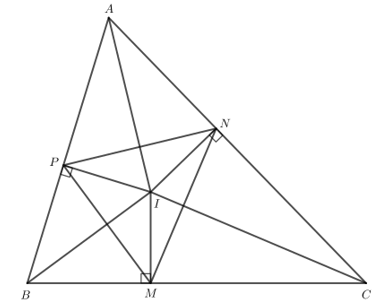
• Chứng minh IA là đường trung trực của NP.

Do IP = IN nên I thuộc đường trung trực của NP.

Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:

AI chung.

IP = IN (theo giả thiết).

Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).

Suy ra AP = AN (2 cạnh tương ứng).

Do AP = AN nên A thuộc đường trung trực của NP.

Do đó IA là đường trung trực của NP.

• Chứng minh IB là đường trung trực của PM.

Do IP = IM nên I thuộc đường trung trực của PM.

Xét ∆BIP vuông tại P và ∆BIM vuông tại M có:

BI chung.

IP = IM (theo giả thiết).

Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).

Suy ra BP = BM (2 cạnh tương ứng).

Do BP = BM nên B thuộc đường trung trực của PM.

Do đó IB là đường trung trực của PM.

• Chứng minh IC là đường trung trực của MN.

Do IM = IN nên I thuộc đường trung trực của MN.

Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:

CI chung.

IM = IN (theo giả thiết).

Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).

Suy ra CM = CN (2 cạnh tương ứng).

Do CM = CN nên C thuộc đường trung trực của MN.

Do đó IC là đường trung trực của MN.