Câu 1: Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Kết luận đúng là

• A. GM = GN;
• B. $GM=\frac{1}{3}GB$

• C. $GN=\frac{1}{2}GC$

• D. GB = GC.

Câu 2: Cho hình vẽ sau

Điền số thích hợp vào chỗ chấm : GE = …. BE.

• A. 2;
• B. 3;
• C. $\frac{2}{3}$

• D. $\frac{1}{3}$

Câu 3: Cho tam giác ABC, đường trung tuyến BD. Trên tia đối tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC ; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN với BE. Tính BE biết IK = 3 cm

• A. 6 cm

• B. 9 cm

• C. 12 cm
• D. 15 cm

Câu 4: Cho tam giác MNP, hai đường trung tuyến ME và NF cắt nhau tại O. Tính diện tích tam giác MNP, biết diện tích tam giác MNO là 8 cm$^{2}$

• A. 12 cm$^{2}$
• B. 48 cm$^{2}$
• C. 36 cm$^{2}$

• D. 24 cm$^{2}$

Câu 5: CHo tam giác ABC, các đường trung tuyến BD và CE. Chọn câu đúng

• A. $BD + CE<\frac{3}{2}BC$

• B. $BD + CE>\frac{3}{2}BC$

• C. $BD + CE=\frac{3}{2}BC$
• D. BD + CE = BC

Câu 6: Cho hình vẽ sau

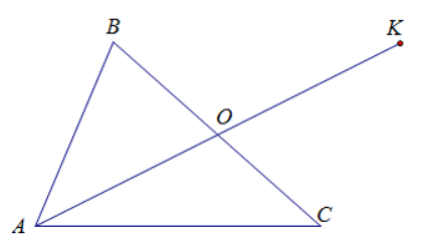
Biết rằng AO là đường trung tuyến của ∆ABC, AO = OK; AB = 6,3 cm; BC = 6,5 cm; AC = 6,7 cm. Độ dài CK bằng

• A. 6,4 cm;
• B. 6,7 cm;
• C. 6,5 cm;

• D. 6,3 cm.

Câu 7: Tam giác ABC có trung tuyến AM = 6 cm và trọng tâm G. Độ dài đoạn AG là

• A. 4.5 cm
• B. 3 cm
• C. 6 cm

• D. 4 cm

Câu 8: Cho ∆ABC vuông tại A. Trung tuyến AK và BH cắt nhau tại M. Trên tia đối của tia KA lấy D sao cho KD = KA. DH cắt BC tại N. Kết luận nào dưới đây sai?

• A. CD // AB;
• B. DC ⊥ AC;
• C. BH = DH;

• D. ∆HMN cân tại M.

Câu 9: Cho tam giác ABC có các đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết BD = 9 cm; CE = 12 cm

• A. BC = 12 cm
• B. BC = 6 cm
• C. BC = 8 cm

• D. BC = 10 cm

Câu 10: Cho ∆ABC, đường trung tuyến AD. Trên tia đối của tia DA lấy điểm K sao cho DK= $\frac{1}{3}$ AD. Qua B vẽ một đường thẳng song song với CK, cắt AC tại M. Gọi G là giao điểm của BM và AD. Khẳng định nào sau đây sai?

• A. DG= $\frac{1}{3}$ AD

• B. MA < MC;

• C. ∆BDG = ∆CDK;
• D. BG = CK.

Câu 11: Cho G là trọng tâm của tam giác MNP với đường trung tuyến MI. Câu nào dưới đây đúng?

• A. $\frac{MG}{MI}=\frac{1}{3}$
• B. $\frac{GI}{MI}=\frac{2}{3}$

• C. $\frac{MG}{GI}=2$

• D. $\frac{GI}{MG}=\frac{2}{3}$

Câu 12: Cho tam giác ABC . Trên tia đối tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. AG cắt BC tại M. Lấy H là trung điểm AG. Nối EG cắt AF tại N. Lấy I là trung điểm EG. Chọn câu đúng

• A. Hai tam giác ABC và AEF có cùng trọng tâm

• B. Hai tam giác ABC và AEC có cùng trọng tâm
• C. Hai tam giác ABC và ABF có cùng trọng tam
• D. Hai tam giác AEM và AMF có cùng trọng tâm

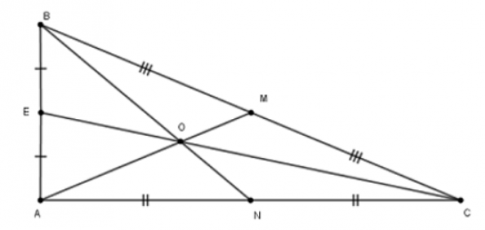
Câu 13: Cho hình vẽ sau

Tính $\frac{GN}{GE}$

• A. 3
• B. $\frac{1}{3}$

• C. $\frac{1}{2}$

• D. 2

Câu 14: Cho tam giác ABC . Trên tia đối tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF. Gọi G là trọng tâm tam giác ABC. AG cắt BC tại M. Lấy H là trung điểm AG. Nối EG cắt AF tại N. Lấy I là trung điểm EG. Chọn câu đúng

• A. IH // MN; IH = MN

• B. IH // MN; IH < MN
• C. IH // MN; IH > MN
• D. IH // MN; IH = 2MN

Câu 15: Cho tam giác ABC vuông tại A có AB = 5 cm, BC = 13 cm. Ba đường trung tuyến AM , BN, CE cắt nhau tại O

Độ dài trung tuyến BN là

• A. 6 cm

• B. $\sqrt{61}$ cm

• C. 12 cm
• D. $\sqrt{65}$ cm

Câu 16: Cho tam giác ABC có các đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết BD = 4.5 cm; CE = 6 cm

• A. BC = 6 cm
• B. BC = 4.5 cm

• C. BC = 5 cm

• D. BC = 10 cm

Câu 17: Cho tam giác ABC, đường trung tuyến BD. Trên tia đối tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC ; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN với BE. Chọn câu đúng

• A. BI = IK > KE
• B. BI > IK > KE

• C. BI = IK = KE

• D. BI < IK < KE

Câu 18: Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD = CE. Khi đó tam giác ABC

• A. Cân tại B
• B. Cân tại C
• C. Vuông tại A

• D. Cân tại A

Câu 19: Cho G là trọng tâm của tam giác đều. Chọn câu đúng

• A. GA = GB = GC

• B. GA = GB > GC
• C. GA < GB < GC
• D. GA > GB > GC

Câu 20: Cho G là trọng tâm của tam giác đều ABC. D, E., F lần lượt là trung điểm của BC, AC, AB. Chọn câu đúng

• A. GD > GE > GF
• B. GD < GE < GF
• C. GD > GE = GF

• D. GD = GE = GF