BÀI 4: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

I. PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG

LT-VD 1 trang 32 sgk toán 11 cánh diều

Hai phương trình x−1=0 và có tương đương không? Vì sao?

Giải nhanh:

+ Ta có:

Tập nghiệm của phương trình là

+ Ta có:

ĐKXĐ:

Tập nghiệm của phương trình là

=> Ta thấy nên hai phương trình trên tương đương

LT-VD 2 trang 33 sgk toán 11 cánh diều

Giải phương trình: (x−1)² = 5x−11

Giải nhanh:

(x – 1)² = 5x – 11

⇔ x² – 2x + 1 – (5x – 11) = 0

⇔ x² – 7x + 12 = 0

⇔

Như vậy tập nghiệm của phương trình đã cho là S = {3; 4}

II. PHƯƠNG TRÌNH SINX = M

LT-VD 3 trang 34 sgk toán 11 cánh diều

a) Giải phương trình: sinx =

b) Tìm góc lượng giác x sao cho sinx = sin55^∘

Giải nhanh:

a) 

b)  

III. PHƯƠNG TRÌNH COSX = M

LT-VD 4 trang 35 sgk toán 11 cánh diều

Giải phương trình

Giải nhanh:

LT-VD 5 trang 36 sgk toán 11 cánh diều

a) Giải phương trình: cosx = −1/2.

b) Tìm góc lượng giác x sao cho cosx = (−87^∘)

Giải nhanh:

a)

b) 

LT-VD 6 trang 37 sgk toán 11 cánh diều

Giải phương trình được nêu trong bài toán mở đầu.

Giải nhanh:

+)  

+)  

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp 

Ta được kết quả gần đúng là 2,3).

+)  

IV. PHƯƠNG TRÌNH TANX = M

LT-VD 7 trang 37 sgk toán 11 cánh diều

a) Giải phương trình: tanx = 0.

b) Tìm góc lượng giác x sao cho tanx = tan67^∘

Giải nhanh:

a)

b) ,

V. PHƯƠNG TRÌNH COTX = M

LT-VD 8 trang 38 sgk toán 11 cánh diều

a) Giải phương trình: cotx = 1. 

b) Tìm góc lượng giác x sao cho cotx = cot(−83^∘). 

Giải nhanh:

a)

b) ,

VI. GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN BẰNG MÁY TÍNH CẦM TAY

LT-VD 9 trang 39 sgk toán 11 cánh diều

Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian (làm tròn kết quả đến hàng phần nghìn):

a) sinx = 0,2

b) cosx =

c) tanx =

Giải nhanh:

Sau khi chuyển máy tính sang chế độ “radian”.

a) Bấm:

Ta được kết quả gần đúng là 0,201.

Vậy phương trình sinx = 0,2 có các nghiệm là:

và 

.

b)  Bấm:

Ta được kết quả gần đúng là 1,772.

Vậy phương trình có các nghiệm là: 

.

c) Bấm:

Ta được kết quả gần đúng là 0,955.

Vậy phương trình có các nghiệm là: .

BT 1 trang 40 sgk toán 11 cánh diều

Giải phương trình:

a)

b)

c)

d)

e)

g)

Giải nhanh:

a)

b)

c)

d)

e)

g)  

BT 2 trang 40 sgk toán 11 cánh diều

Giải phương trình:

a)

b)

c)

Giải nhanh:

a)

b)

c)  

BT 3 trang 40 sgk toán 11 cánh diều

Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:

a) 3sinx+2=0 trên khoảng

b) cosx=0 trên đoạn []

Giải nhanh:

a) Ta có:

Đường thẳng và đồ thị hàm số trên khoảng được vẽ như sau:

Đường thẳng cắt đồ thị trên khoảng tại 5 điểm A, B, C, D, E

Như vậy phương trình có 5 nghiệm trên khoảng

b) Đường thẳng y = 0 (trục Ox) và đồ thị hàm số trên đoạn được vẽ như sau:

Đường thẳng y = 0 cắt đồ thị hàm số trên đoạn tại 6 điểm M, N, P, Q, I, K

Như vậy phương trình có 6 nghiệm trên đoạn

BT 4 trang 40 sgk toán 11 cánh diều

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40∘ Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:

d(t) = 3sin[ π/182.(t−80) ] + 12 với t ∈ Z và 0 < t ≤ 365. 

a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm? 

b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?

c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?

Giải nhanh:

a) Để thành phố A có đúng 12 giờ có ánh sáng mặt trời thì:

Do và nên ta có:

Với k = 0 thì t = 80 + 182.0 = 80

Với k = 1 thì t = 80 + 182.1 = 262

Như vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và ngày thứ 262 trong năm

b) Để thành phố A có đúng 9 giờ có ánh sáng mặt trời thì:

Do và nên ta có :

Với k = 1 thì t = ‒11 + 364.1 = 353

Như vậy thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353 trong năm.

c) Để thành phố A có đúng 15 giờ có ánh sáng mặt trời thì:

Do và nên ta có :

Với k = 0 thì t = 171 + 364.0 = 171

Như vậy thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171 trong năm

BT 5 trang 40 sgk toán 11 cánh diều

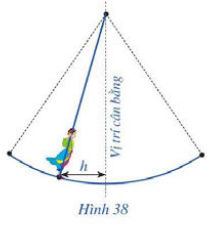
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với t ≥ 0) bởi hệ thức h = |d| với d = 3cos[ π/3.(2t−1) ], trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian t nào thì khoảng cách h là 3 m; 0 m?

Giải nhanh:

• Để khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng là 3 m thì:

=>

Do nên k ∈ {0; 1; 2; …}

Khi đó

Vậy (giây) thì khoảng cách h là 3 m.

• Để khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng là 0 m thì:

Do t ≥ 0, k ∈ ℤ nên k ∈ {0; 1; 2; …}, khi đó

Vậy (giây) thì khoảng cách h là 0 m.