Câu 1: Cho hàm số $f(x) = mx^{2} – 2mx + m – 1$. Giá trị của m để f(x) < 0 ∀x ∈ ℝ.

• A. m ≥ 0;
• B. m > 0;
• C. m < 0;

• D. m ≤ 0.

Câu 2: Bảng xét dấu nào sau đây là bảng xét dấu của tam thức $f(x) = x^{2} + 2x + 1$ là:

• A. 
• B. 
• C. 

• D. 

Câu 3: Xác định m để biểu thức $f(x) = (m + 2)x^{2} – 3mx + 1$ là tam thức bậc hai

• A. m = 2;
• B. m = – 2;
• C. m ≠ 2;

• D. m ≠ – 2.

Câu 4: Các giá trị m làm cho biểu thức f(x) = x$^{2}$ + 4x + m + 3 luôn dương là

• A. m < 1;
• B. m ≥ 1;

• C. m > 1;

• D. m ∈ ∅.

Câu 5: Cho tam thức $f(x) = x^{2} + 2mx + 3m – 2$. Tìm m để f(x) ≥ 0 với mọi x ∈ ℝ.

• A. 1 ≤ m ≤ 2;

• B. 1 < m < 2;
• C. m < 1;
• D. m > 2.

Câu 6: Cho tam thức $f(x) = ax^{2} + bx + c$ (a ≠ 0), có ∆ = b2 – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:

• A. a < 0 và ∆ ≤ 0;           

• B. a ≤ 0 và ∆ < 0;            
• C. a < 0 và ∆ ≥ 0;            
• D. a > 0 và ∆ ≤ 0.

Câu 7: Cho tam thức bậc hai $f(x) = x^{2} – 10x + 2$. Kết luận nào sau đây đúng?

• A. f(–2) < 0;         
• B. f(1) > 0;            

• C. f(–2) > 0;          

• D. f(1) = 0.

Câu 8: Cho tam thức bậc hai $f(x) = ax^{2} + bx + c$ có đồ thị như hình vẽ dưới đây

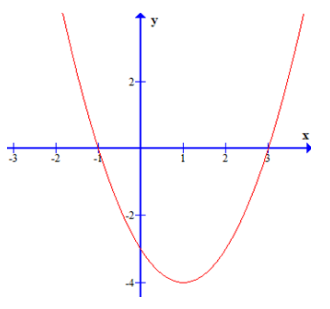
Bảng biến thiên của tam thức bậc hai là

• A. 

• B. 
• C. 
• D. 

Câu 9: Biểu thức nào sau đây là tam thức bậc hai?

• A. $f(x) = 2x^{3} + 3x^{2} + 1$;           

• B. $f(x) = –x^{2} + 2x – 10$;             

• C. f(x) = x – 4;                
• D. f(x) = –7.

Câu 10: Tìm tất cả các giá trị của m để tam thức $f(x) = mx^{2} – x + m$ luôn dương với ∀x ∈ ℝ

• A.m > 0;
• B. m < 0;

• C. $m>\frac{1}{2}$

• D. $m<\frac{1}{2}$

Câu 11: Tam thức nào sau đây nhận giá trị âm với mọi x < 1

• A. $f(x) = x^{2} – 5x +6 $;
• B. $f(x) = x^{2} – 16$;
• C. $f(x) = x^{2} + 2x + 3$;

• D. $f(x) = – x^{2} + 5x – 4$.

Câu 12: Biểu thức nào sau đây là tam thức bậc hai

• A. f(x) = x + 2;
• B. $f(x) = 2x^{3} + 2x^{2} – 1;$

• C. $f(x) = x^{2} – 3x;$

• D. f(x) = 2x – 1.

Câu 13: Tam thức $y = – x^{2} – 3x – 4$ nhận giá trị âm khi và chỉ khi

• A. x < 4 hoặc x > – 1;
• B. x < 1 hoặc x > 4;
• C. – 4 < x < 4;

• D. x ∈ ℝ.

Câu 14: Biểu thức $f(x) = (m^{2} + 2)x^{2} – 2(m – 2)x + 2$ luôn nhận giá trị dương khi và chỉ khi

• A. m ≤ - 4 hoặc m ≥ 0;

• B. m < - 4 hoặc m > 0;

• C. – 4 < m < 0;
• D. m < 0 hoặc m > 4.

Câu 15: Biệt thức và biệt thức thu gọn của tam thức bậc hai $f(x) = –x^{2} – 4x – 6$ lần lượt là:

• A. ∆ = –2 và ∆’ = –8;                
• B. ∆’ = –8 và ∆ = –2;                
• C. ∆ = 8 và ∆’ = 2;          

• D. ∆ = –8 và ∆’ = –2.

Câu 16: Với x thuộc tập hợp nào dưới đây thì đa thức $f(x) = x^{2} – 6x + 8$ không dương?

• A. [2; 3];
• B. (−∞;2)∪(4;+∞)
  

• C. [2; 4];

• D. [1; 4].

Câu 17: Nghiệm của tam thức bậc hai $f(x) = –2x^{2} + 4x – 2$ là:

• A. x = 1;               

• B. x = 1 hoặc x = –1;                
• C. x = –1;             
• D. f(x) vô nghiệm.

Câu 18: Các giá trị m để tam thức $f(x) = x^{2} – (m + 2)x + 8m + 1$ đổi dấu 2 lần là

• A. m ≤ 0 hoặc m ≥ 28;

• B. m < 0 hoặc m > 28;

• C. 0 < m < 28;
• D. m > 0.

Câu 19: Cho $f(x) = (3m – 2)x^{2} – 2(3m – 2)x + 3(2m + 1)$. Đa thức f(x) là tam thức bậc hai khi và chỉ khi:

• A. $m<\frac{2}{3}$

• B. $m\neq \frac{2}{3}$

• C. $m>\frac{2}{3}$
• D. $m=\frac{2}{3}$

Câu 20: Cho $f(x) = mx^{2} – 2x – 1$. Xác định m để f(x) < 0 với mọi x ∈ ℝ.

• A. m < – 1;

• B. m < 0;
• C. – 1 < m < 0;
• D. m < 1 và m ≠ 0.