Câu 1: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

• A. $\left\{\begin{matrix}x<1\\ y-1>2\end{matrix}\right.$

• B. $\left\{\begin{matrix}x^{2}+y<0\\ y-x>0\end{matrix}\right.$
• C. y - 2x <0
• D. $\left\{\begin{matrix}2x-y^{2}<5\\ 4x+3y>10^{10}\end{matrix}\right.$

Câu 2: Tìm m để hệ bất phương trình sau trở thành hệ bất phương trình bậc nhất hai ẩn: $\left\{\begin{matrix}mx^{2}+2(m+1)x+y<1\\ my^{2}+3x-4y-1>0\end{matrix}\right.$

• A. m = ‒1;

• B. m = 0;

• C. m = 1;
• D. m = 2.

Câu 3: Khoảng giá trị của x khi y = 1 trong hệ bất phương trình $\left\{\begin{matrix}x+y\geq 1\\ 2x-3y<5\end{matrix}\right.$là:

• A. x ∈ [0; 4);

• B. x ∈ (0; 4];
• C. x ∈ (1; 5);
• D. x ∈ [1; 5].

Câu 4: Cặp số nào sau đây là nghiệm của hệ bất phương trình $\left\{\begin{matrix}x+y>4\\ x-y<10\end{matrix}\right.$?

• A. (2; 1);

• B. (10; 2);

• C. (‒3; 4);
• D. (0; ‒10).

Câu 5:  Cho hệ bất phương trình $\left\{\begin{matrix}x+5y<1\\ 5x-4y>6\end{matrix}\right.$. Hỏi khi cho y = 0, x có thể nhận mấy giá trị nguyên nào?

• A. 0;

• B. 1;
• C. 2;
• D. 3.

Câu 6: Cho hệ bất phương trình $\left\{\begin{matrix}x+2y\leq 6\\ 3x-y\leq 12\\ x\geq 0\\ y\geq 0\end{matrix}\right.$ có miền nghiệm là miền tứ giác OABC như hình dưới. Giá trị lớn nhất của F = 28x + 49y là:

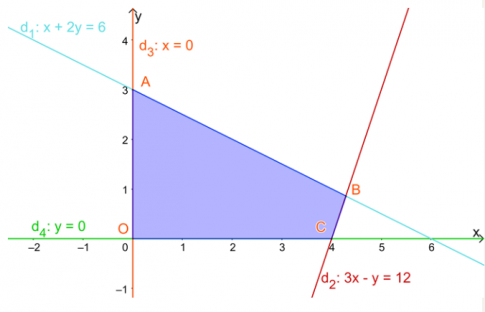
• A. 0
• B. 112
• C. 147

• D. 162

Câu 7: Cho hệ bất phương trình $\left\{\begin{matrix}2x+y\leq 6\\ 3x+4y\leq 6 \\ 5x-2y\geq 0\\x\leq 2 \\ y\geq -1 \end{matrix}\right.$ có miền nghiệm là miền ngũ giác ABCDE như hình dưới. Giá trị nhỏ nhất của F = 12x -39y là:

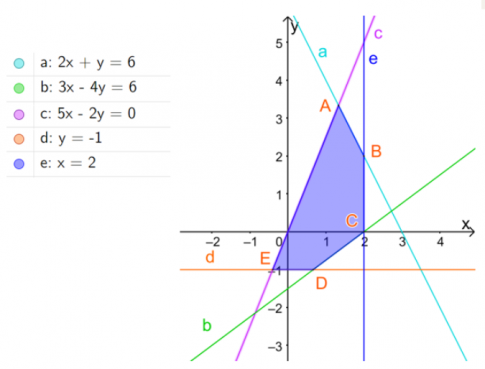
• A. -30

• B. -10

• C. 12
• D. 19

Câu 8: Cho hệ bất phương trình $\left\{\begin{matrix}x\geq 0 \\ y\geq 0 \\ x+y\leq 80 \\ 2x+y\leq 120\end{matrix}\right.$

Trong các cặp số (-1; -1), (-1; 0), (1; 1), (2; 2), (0; -1) thì những cặp số là nghiệm của hệ bất phương trình trên là:

• A. (-1; -1), (-1; 0);
• B. (1; 1), (-1; 0);

• C. (1; 1), (2; 2);

• D. (0; -1), (1; 1).

Câu 9: Phần tô màu trong hình dưới đây biểu diễn miền nghiệm của hệ bất phương trình nào?

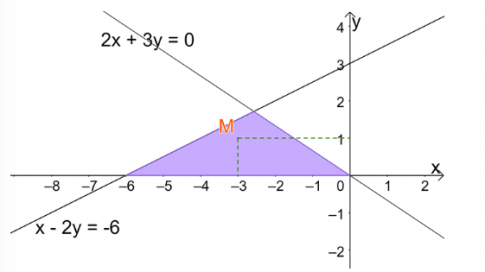
• A. $\left\{\begin{matrix}x-2y+6\leq 0 \\ 2x-3y\geq 0\\ x\geq 0\end{matrix}\right.$
• B. $\left\{\begin{matrix}x-2y+6\geq 0 \\ 2x-3y\leq 0\\ x\geq 0\end{matrix}\right.$
• C. $\left\{\begin{matrix}x-2y+6\geq 0 \\ 2x-3y\geq 0\\ x\leq 0\end{matrix}\right.$

• D. $\left\{\begin{matrix}x-2y+6\geq 0 \\ 2x-3y\leq 0\\ x\leq 0\end{matrix}\right.$

Câu 10: Điểm M(0; -3) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

• A. $\left\{\begin{matrix}2x-y\leq 3\\ 2x+5y\leq 12x+8\end{matrix}\right.$

• B. $\left\{\begin{matrix}2x-y> 3\\ 2x+5y\leq 12x+8\end{matrix}\right.$
• C. $\left\{\begin{matrix}2x-y>- 3\\ 2x+5y\leq 12x+8\end{matrix}\right.$
• D. $\left\{\begin{matrix}2x-y\leq -3\\ 2x+5y\leq 12x+8\end{matrix}\right.$

Câu 11: Điểm M(1; 0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

• A. $\left\{\begin{matrix}2x+y>1\\ x+y>2\end{matrix}\right.$

• B. $\left\{\begin{matrix}2x+y>1\\ x+y>0\end{matrix}\right.$

• C. $\left\{\begin{matrix}2x+y>1\\ x+y>3\end{matrix}\right.$
• D. $\left\{\begin{matrix}2x+y>1\\ x+y>4\end{matrix}\right.$

Câu 12: Khẳng định nào sau đây là sai?

• A. Hệ bất phương trình bậc nhất hai ẩn luôn có ít nhất 2 bất phương trình bậc nhất 2 ẩn;
• B. Hệ bất phương trình $\left\{\begin{matrix}x+y\geq 1\\ 2x-3y<5\end{matrix}\right.$ nghiệm là (x; y) = (0; 1);

• C. Hệ bất phương trình bậc nhất hai ẩn luôn có miền nghiệm là một đa giác;

• D. Hệ bất phương trình có thể vô nghiệm.

Câu 13: Cho hệ bất phương trình:$\left\{\begin{matrix}2x+y>0\\ x+y>3\end{matrix}\right.$, điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình đã cho?

• A. O(0; 0);

• B. M(2; 3);
• C. N(3; 4);
• D. P(4; 5).

Câu 14: Cặp số nào sau đây là nghiệm của hệ bất phương trình $\left\{\begin{matrix}3x-5y>12\\ x-2y\leq 7\end{matrix}\right.$

• A. (0;3)

• B. (6;1)

• C. (2;4)
• D. (3;2)

Câu 15:  Cho hệ bất phương trình $\left\{\begin{matrix}x\geq 0 \\ y\geq 0\\ 0.5x+y\leq 8 \end{matrix}\right.$. Miền nghiệm của hệ bất phương trình biểu diễn bởi miền tam giác OAB. Ba điểm nào sau đây có tọa độ đúng của O, A và B?

• A. O(0; 0), A(0; 8), B(16; 0);

• B. O(0; 0), A(8; 0), B(16; 0);
• C. O(0; 0), A(0; 8), B(0; 16);
• D. O(0; 0), A(8; 8), B(16; 0).

Câu 16: Một nhà khoa học nghiên cứu về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. Kết quả như sau:

- Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.

- Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B.

Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn $\frac{1}{2}$ số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A.

Biết giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng. Phương án dùng hai loại vitamin A, B thoả mãn các điều kiện trên để có số tiền phải trả là ít nhất là:

• A. 500 đơn vị vitamin A và 500 đơn vị vitamin B;
• B. 600 đơn vị vitamin A và 400 đơn vị vitamin B;
• C. 600 đơn vị vitamin A và 300 đơn vị vitamin B;

• D. 100 đơn vị vitamin A và 300 đơn vị vitamin B.

Câu 17: Miền nghiệm của hệ bất phương trình $\left\{\begin{matrix}x+2(y+1)-4y\leq 2(x+1)-5y\\ x+y\geq 0\end{matrix}\right.$

• A. (1;-1)

• B. (1;0)
• C. (3;2)
• D. (0;3)

Câu 18: Bác An cần phải làm nến trong vòng không quá 8 giờ để bán. Nến loại A cần 30 phút để làm xong một cây, nến loại B cần 1 giờ để làm xong một cây. Gọi x, y lần lượt là số nến loại A, B bác An sẽ làm được. Hệ bất phương trình mô tả điều kiện của x và y là hệ bất phương trình nào sau đây?

• A. $\left\{\begin{matrix}x\geq 0 \\ y\geq 0\\ 0.5x+y>8\end{matrix}\right.$

• B. $\left\{\begin{matrix}x\geq 0 \\ y\geq 0\\ 0.5x+y\leq 8\end{matrix}\right.$

• C. $\left\{\begin{matrix}x\geq 0 \\ y< 0\\ 0.5x+y\leq 8\end{matrix}\right.$
• D. $\left\{\begin{matrix}x> 0 \\ y> 0\\ 0.5x+y\leq 8\end{matrix}\right.$

Câu 19: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki ‒ lo ‒ gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi ki ‒ lo ‒ gam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Giá trị x2 + y2 là:

• A. 1;
• B. 1,2;

• C. 1,3;

• D. 1,5.

Câu 20: Cho hệ bất phương trình bậc nhất hai ẩn: $\left\{\begin{matrix}x\geq 0 \\ y\geq 0 \\ x+y\leq 100 \\ 2x+y\leq 120 \end{matrix}\right.$

Và F(x; y) = 3,5x + 2y. Tìm giá trị lớn nhất của F(x; y).

• A. 210;

• B. 230;

• C. 200;
• D. 270.