I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HĐ1: Hệ bất phương trình:

${\left\{\begin{matrix}
x-y<3 & &(1) \\
x+2y> -2& & (2)
\end{matrix}\right.}$

a) Mỗi bất phương trình (1) và (2) đều là bất phương trình bậc nhất hai ẩn.

b) Chọn $x_o= 2, y_o= 1$. Khi đó: 

(1) ⇔ 2 – 1 < 3 ⇔ 1 < 3 mệnh đề đúng nên (2; 1) là nghiệm của bất phương trình (1).

(2) ⇔ 2 + 2.1 > – 2 ⇔ 4 > – 2 mệnh đề đúng nên (2; 1) là nghiệm của bất phương trình (2).

Vậy cặp số (2; 1) là một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên. 

Kết luận:

Hệ bất phương trình bậc nhất ẩn x, y là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.

Ví dụ 1 (SGK - tr25, 26)

Luyện tập 1:

Hệ bất phương trình:

$\left\{\begin{matrix}
2x+y >0& & & \\
x-3y <6& & & \\
x-y \geq -4& & &
\end{matrix}\right.$

Thay x = 1; y = 0 vào 3 bất phương trình của hệ, ta có:

2.1 + 0 = 2 > 0 là mệnh đề đúng; 

1 − 3. 0 = 1 < 6 là mệnh đề đúng; 

1 − 0 = 1 ≥ −4 là mệnh đề đúng.

Vậy (1; 0) là nghiệm chung của 3 bất phương trình nên (1; 0) là nghiệm của hệ bất phương trình.

II. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Miền nghiệm của hệ bất phương trình là giao các miền nghiệm của các bất phương trình trong hệ.

HĐ2: (SGK - tr26)

Kết luận: Để biểu diễn miền nghiệm của hệ bất phương trình hai ẩn, ta làm như sau:

+ Trong cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm đó.

+ Phần không bị gạch là miền nghiệm cần tìm.

Ví dụ 2 (SGK - tr27)

Luyện tập 2:

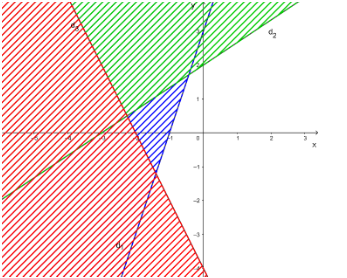
Hệ bất phương trình:

$\left\{\begin{matrix}
3x-y> -3& & & \\
-2x+3y<6& & & \\
2x+y> -4& & &
\end{matrix}\right.$

Trên cùng một mặt phẳng tọa độ Oxy, vẽ 3 đường thẳng:

$d_1: 3x – y = – 3$;

$d_2: – 2x + 3y = 6$;

$d_3: 2x + y = – 4$. 

Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. 

Miền nghiệm của hệ bất phương trình là phần mặt phẳng không bị gạch sọc không kể đường biên trong hình dưới. 

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Tổng quát, người ta chứng minh được rằng:

Giá trị lớn nhất (hay nhỏ nhất) của biểu thức F(x; y) = ax + by, với (x; y) là tọa độ các điểm thuộc miền đa giác $A_1A_2...A_n$, tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.

Bài toán 1: (SGK - tr27, 28)

Bài toán 2: (SGK - tr28, 29)