ÔN TẬP CHƯƠNG 8: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN (PHẦN 3)

Câu 1: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa AB và DH.

• A. 45°

• B. 90°

• C. 120°
• D. 60°

Câu 2: Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm Ovà O'. Hãy xác định góc giữa OO’ và AB.

• A. 60°
• B. 45°
• C. 120°

• D. 90°

Câu 3: Cho hình hộp MNPQ.M’N’P’Q’ có góc giữa hai đường thẳng MN và MQ bằng 70°. Góc giữa hai đường thẳng M’N’ và NP bằng góc giữa hai đường thẳng:

• A. MN và MP

• B. MN và MQ

• C. MP và NP
• D. NN’ và NP

Câu 4: Cho hình hộp MNPQ.M’N’P’Q’ có góc giữa hai đường thẳng MN và MQ bằng 70°. Góc giữa hai đường thẳng M’N’ và NP bằng

• A. 60°
• B. 45°
• C. 90°

• D. 70°

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Tính góc giữa AC và MN.

• A. 60°
• B. 45°
• C. 120°

• D. 90°

Câu 6: Cho hai mặt phẳng (P) và(Q) cắt nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?

• A. 1.

• B. 2.
• C. 3.
• D. Vô số.

Câu 7: Cho hai mặt phẳng (P) và (Q), a là một đường thẳng nằm trên(P). Mệnh đề nào sau đây sai ?

• A. Nếu a // b với b=(P)∩(Q) thì a // (Q).

• B. Nếu  (P) ⊥ (Q) thì a ⊥ (Q).

• C. Nếu a cắt (Q) thì (P) cắt (Q).
• D. Nếu (P) // (Q) thì a // (Q).

Câu 8: Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?

• A. 2.
• B. 3.
• C. 1.

• D. Vô số.

Câu 9: Trong các mệnh đề sau, mệnh đề nào đúng?

• A. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc nhọn giữa mặt phẳng (P) và mặt phẳng (R) khi mặt phẳng (Q) song song với mặt phẳng (R).
• B. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc nhọn giữa mặt phẳng (P) và mặt phẳng (R) khi mặt phẳng (Q) song song với mặt phẳng (R) (hoặc (Q)≡(R).
• C. Góc giữa hai mặt phẳng luôn là góc nhọn.

• D. Cả ba mệnh đề trên đều đúng

Câu 10: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy. Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng?

• A. Có ba cặp mặt phẳng vuông góc với nhau.
• B. Có hai cặp mặt phẳng vuông góc với nhau.

• C. Có năm cặp mặt phẳng vuông góc với nhau.

• D. Có bốn cặp mặt phẳng vuông góc với nhau.

Câu 11: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?

• A. (ABE) ⊥ (ADC).

• B. (ABD) ⊥ (ADC).

• C. (ABC) ⊥ (DFK).
• D. (DFK) ⊥ (ADC).

Câu 12: Cho hình lăng trụ ABCD.A’B’C’D’. Hình chiếu vuông góc của A’ lên (ABC) trùng với trực tâm H  của tam giác ABC. Khẳng định nào sau đây không đúng?

• A. BB’C’C là hình chữ nhật.
• B. (AA’H)  ⊥ (A’B’C’).
• C. (BB’C’C) ⊥  ( AA’H).

• D. (AA’B’B) ⊥ (BB’C’C).

Câu 13: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?

• A. SC ⊥ (ABC).

• B. Nếu A' là hình chiếu vuông góc của A lên (SBC) thì A' ∈ SB.

• C. (SAC) ⊥ (ABC).
• D. BK là đường cao của tam giác ABC thì BK ⊥ (SAC).

Câu 14: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác ABC vuông cân ở A và có đường cao AH,(H ∈ BC). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

• A. SC ⊥ (ABC).

• B. (SAH) ⊥ (SBC).

• C. O  ∈  SC.
• D. Góc giữa (SBC) và (ABC) là góc SBA.

Câu 15: Cho tứ diện ABCD có AB ⊥ (BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?

• A. (ADC) ⊥ (ABE).
• B. (ADC) ⊥ (DFK).

• C. (ADC) ⊥ (ABC).

• D. (BDC) ⊥ (ABE).

Câu 16: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ?

• A. Đáy là đa giác đều.
• B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
• C. Các cạnh bên là những đường cao.

• D. Các mặt bên là những hình bình hành.

Câu 17: Cho hình lập phương ABCD.A' B' C'D' có cạnh bằng a. Khẳng định nào sau đây sai?

• A. Tam giác AB' C là tam giác đều.
• B. Nếu α là góc giữa AC' và (ABCD) thì .

• C. ACC'A' là hình chữ nhật có diện tích bằng 2a².

• D. Hai mặt (AA' C' C) và (BB' D'D) ở trong hai mặt phẳng vuông góc với nhau.

Câu 18: Cho hình lập phương ABCD.A' B' C' D' cạnh bằng a. Khẳng định nào sau đây sai?

• A. Hai mặt ACC' A' và BDD'B' vuông góc nhau.
• B. Bốn đường chéo AC', A'C, BD', B'D bằng nhau và bằng

• C. Hai mặt ACC'A' và BDD'B' là hai hình vuông bằng nhau.

• D. AC ⊥ BD'.

Câu 19: Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?

• A. (AA' B' B) ⊥ (BB'C'C).

• B. (AA' H) ⊥ (A' B'C').
• C. BB' C' C là hình chữ nhật.
• D. (BB' C'C) ⊥ (AA'H).

Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA=a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu?

• A. 30⁰
• B. 45⁰
• C. 90⁰

• D. 60⁰

Câu 21: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a; CD=2x. với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.

• A. .

• B. .
• C. .
• D. .

Câu 22: Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B,C lần lượt lấy D, E nằm trên cùng một phía đối với (P) sao cho . Góc giữa (P) và (ADE) bằng bao nhiêu?

• A. 30⁰

• B. 60⁰

• C. 90⁰
• D. 45⁰

Câu 23: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C trên (P), D trên (Q) sao cho AC ⊥ AB, BD ⊥ AB,  và AB=AC=BD=a. Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua A' và vuông góc với CD là?

• A.
• B.

• C.

• D.

Câu 24: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a, CD=2x. Gọi I, J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?

• A. .

• B. .

• C. .
• D. .

Câu 25:  Cho tam giác ABC và mặt phẳng (P) Biết góc giữa mặt phẳng (P) và mặt phẳng (ABC) là φ. Hình chiếu của tam giác ABCtrên mặt phẳng (P) là tam giác A'B'C'. Tìm hệ thức liên hệ giữa diện tích tam giác ABC và diện tích tam giác A'B'C'

• A.
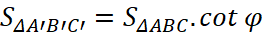
• B.
• C.

• D.