Dễ hiểu giải Toán 11 Kết nối Bài 16 Giới hạn của hàm số
Giải dễ hiểu Bài 16 Giới hạn của hàm số. Trình bày rất dễ hiểu, nên tiếp thu Toán 11 Kết nối dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 16. GIỚI HẠN CỦA HÀM SỐ
1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
Bài 1: Nhận biết khái niệm giới hạn tại một điểm
Cho hàm số ![]()
a) Tìm tập xác định của hàm số f(x)
b) Cho dãy số xn = ![]() . Rút gọn f(xn) và tính giới hạn của dãy (un) với un = f(xn)
. Rút gọn f(xn) và tính giới hạn của dãy (un) với un = f(xn)
c) Với dãy số (xn) bất kì sao cho xn≠2 và xn→2, tính f(xn) và tìm limn→+∞f(xn)
Giải nhanh:
a) ![]()
b) 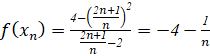
![]()
c) ![]()
Vì ![]() và
và ![]() với mọi
với mọi ![]() nên
nên ![]()
=> limn→+∞![]()
Bài 2: Tính limn->1![]()
Giải nhanh:
limn->1 ![]() limn->1
limn->1![]() = 2
= 2
Bài 3: Nhận biết khái niệm giới hạn một bên
Cho hàm số f(x) = ![]()
a) Cho ![]() và
và ![]() . Tính yn = f(xn) và y’n = f(x’n)
. Tính yn = f(xn) và y’n = f(x’n)
b) Tìm giới hạn của các dãy số (yn) và (y’n)
c) Cho các dãy số (xn) và (x′n) bất kì sao cho x0< 1 < x′n và xn→1, x′n→1, tính limn->+∞ f(xn) và limn->+∞ f(x’n)
Giải nhanh:
a) ![]()
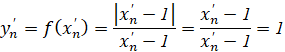
b) limn->+∞ yn = -1
limn->+∞ y’n = 1
c) limn->+∞ f(xn) = -1
limn->+∞ f(x’n) = 1
Bài 4: Cho hàm số f(x) = -x nếu x < 0 và ![]() nếu x ≥ 0. Tính limn->0+ f(xn); limn->0- f(xn) và limn->0 f(xn)
nếu x ≥ 0. Tính limn->0+ f(xn); limn->0- f(xn) và limn->0 f(xn)
Giải nhanh:
limn->0+ f(xn) = 0
limn->0- f(xn) = 0
limn->0 f(xn) = 0
2. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
Bài 1: Nhận biết khái niệm giới hạn tại vô cực. Cho hàm số f(x) = 1+ ![]() có đồ thị như hình 5.4
có đồ thị như hình 5.4
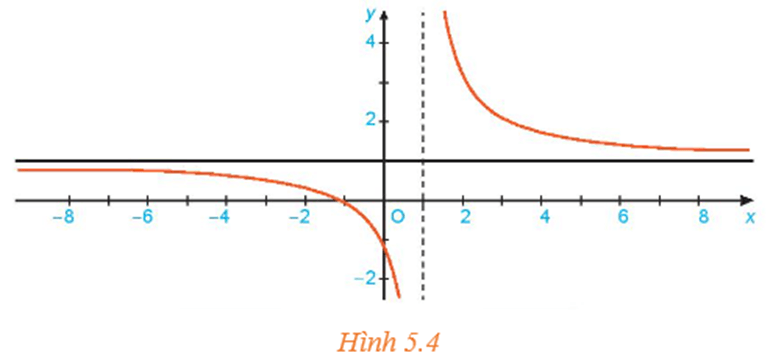
Giả sử (xn) là dãy số sao cho x0 > 1, xn ⟶ +∞. Tính f(xn) và tìm
Giải nhanh:
Với ![]() là dãy số sao cho
là dãy số sao cho ![]()
Ta có: ![]()
Khi ![]() thì
thì ![]()
Do đó lim![]()
![]()
Bài 2: Tính limx-> +![]()
![]()
Giải nhanh:
limx-> +![]()
![]() = limx-> +
= limx-> +![]()
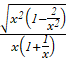
=limx-> +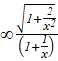 = limx-> +
= limx-> +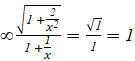
Bài 3: Cho tam giác vuông OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h.
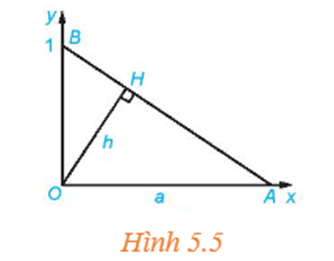
a) Tính h theo a.
b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?
Giải nhanh:
a) ![]() .
.
b) Khi điểm ![]() dịch chuyển về
dịch chuyển về ![]() , ta có
, ta có ![]() , suy ra
, suy ra ![]() , do đó điểm
, do đó điểm ![]() dịch chuyển về điểm
dịch chuyển về điểm ![]() .
.
c) Khi ![]() dịch chuyển ra vô cực theo chiều dương của trục
dịch chuyển ra vô cực theo chiều dương của trục ![]() , ta có
, ta có ![]() .
.
Ta có: lima-> +![]() = lima-> +
= lima-> +![]()
= lima-> +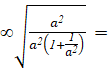 lima-> +
lima-> +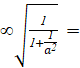 1
1
Do đó điểm ![]() dịch chuyển về
dịch chuyển về ![]() .
.
. Giới hạn vô cực của hàm số tại một điểm
3. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI MỘT ĐIỂM
Bài 4: Nhận biết khái niệm giới hạn vô cực
Xét hàm số ![]() có đồ thị như Hình 5.6.
có đồ thị như Hình 5.6.
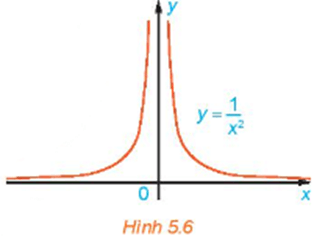
Cho ![]() , chứng tỏ rằng f(xn) ⟶ +∞.
, chứng tỏ rằng f(xn) ⟶ +∞.
Giải nhanh:
Ta có: ![]() , do đó
, do đó ![]()
Vì ![]() nên
nên ![]() và
và ![]()
Bài 5: Cho hàm số ![]() Với các dãy số (xn) và (x’n) cho bởi xn = 1 +
Với các dãy số (xn) và (x’n) cho bởi xn = 1 +![]() , x’n = 1 -
, x’n = 1 - ![]() , tính lim n-> +
, tính lim n-> +![]() f(xn) và lim n-> +
f(xn) và lim n-> +![]() f(x’n)
f(x’n)
Giải nhanh:
lim n-> +![]() f(xn) = +∞
f(xn) = +∞
lim n-> +![]() f(x’n) = -∞
f(x’n) = -∞
Bài 6: Tính các giới hạn sau:
a) lim x-> 0 = ![]()
b) lim x-> 2- =![]()
Giải nhanh:
a) ![]()
b) ![]()
Bài 7: Tính lim x->2+ ![]() và lim x->2-
và lim x->2- ![]()
Giải nhanh:
lim x->2+ ![]() =
= ![]()
lim x->2- ![]() =
= ![]()
BÀI TẬP CUỐI SGK
Bài tập 5.7: Cho hai hàm số ![]() và g(x) = x+1. Khẳng định nào sau đây là đúng?
và g(x) = x+1. Khẳng định nào sau đây là đúng?
a) f(x) = g(x)
b) ![]()
Giải nhanh:
+) Biểu thức ![]() có nghĩa khi
có nghĩa khi ![]()
![]()
![]() có nghĩa với mọi x.
có nghĩa với mọi x.
Do điều kiện xác định của hai hàm số ![]() và
và ![]() khác nhau.
khác nhau.
=> Khẳng định a sai.
+) Ta có : Lim(x->1)![]()
Lim(x->1)![]()
Vậy ![]() nên khẳng định b là đúng
nên khẳng định b là đúng
Bài tập 5.8: Tính các giới hạn sau
a) Limx->0 ![]()
b) Limx->0![]()
Giải nhanh:
a) Limx->0 ![]() = Limx->0
= Limx->0![]() = Limx->0
= Limx->0![]() , với
, với ![]()
b) Limx->0 ![]() Limx->0
Limx->0![]() = Limx->0
= Limx->0![]()
Bài tập 5.9: Cho hàm số H(t) = 0 nếu t<0 và 1 nếu t ≥ 0 (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/ mở của dòng điện tại thời điểm t = 0).Tính limt->0+H(t) và limt->0-H(1)
Giải nhanh:
limt->0+ ![]()
limt->0- ![]()
Bài tập 5.10: Tính các giới hạn một bên
a) limt->1+ ![]()
b) limt->4- ![]()
Giải nhanh:
a) limt->1+ ![]()
![]()
b) limt->4- ![]()
Bài tập 5.11: Cho hàm số ![]() . Tìm limt->2+ g(x) và limt->2- g(x)
. Tìm limt->2+ g(x) và limt->2- g(x)
Giải nhanh:
+) limt->2+ g(x) = -1
+) limt->2- g(x) = 1
Bài tập 5.12: Tính các giới hạn sau:
a) limt->+![]()
b) limt->+![]()
![]()
Giải nhanh:
a) limt->+![]() = -2
= -2
b) limt->+![]()
![]()
Bài tập 5.13: Cho hàm số ![]() . Tìm limt->2+ f(x) và limt->2- f(x)
. Tìm limt->2+ f(x) và limt->2- f(x)
Giải nhanh:
+) limt->2+ f(x) = ![]()
+) limt->2- f(x) = ![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận