BÀI TẬP CUỐI CHƯƠNG I

A - TRẮC NGHIỆM

Bài tập 1.23: Biểu diễn các góc lượng giác trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?

A. β và γ.

B. α, β, γ.

C. β, γ, δ.

D. α và β.

Giải nhanh:

A. β và γ

Bài tập 1.24: Trong các khẳng định sau, khẳng định nào là sai?

A. sin(π – α) = sin α.

B. cos(π – α) = cos α.

C. sin(π + α) = – sin α.

D. cos(π + α) = – cos α.

Giải nhanh:

A. sin(π – α) = sin α.

Bài tập 1.25: Trong các khẳng định sau, khẳng định nào là sai?

A. cos(a – b) = cos a cos b – sin a sin b.

B. sin(a – b) = sin a cos b – cos a sin b.

C. cos(a + b) = cos a cos b – sin a sin b.

D. sin(a + b) = sin a cos b + cos a sin b.

Giải nhanh:

A. cos(a – b) = cos a cos b – sin a sin b

Bài tập 1.26: Rút gọn biểu thức M = cos(a + b) cos(a – b) – sin(a + b) sin(a – b), ta được:

A. M = sin 4a.

B. M = 1 – 2 cos² a.

C. M = 1 – 2 sin² a.

D. M = cos 4a.

Giải nhanh:

C. M = 1 – 2 sin² a.

Bài tập 1.27: Khẳng định nào sau đây là sai?

A. Hàm số y = cos x có tập xác định là ℝ.

B. Hàm số y = cos x có tập giá trị là [– 1; 1].

C. Hàm số y = cos x là hàm số lẻ.

D. Hàm số y = cos x tuần hoàn với chu kì 2π.

Giải nhanh:

C. Hàm số y = cos x là hàm số lẻ.

Bài tập 1.28: Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?

A. y = tan x + x.

B. y = x² + 1.

C. y = cot x.

D. y =

Giải nhanh:

C. y = cot x.

Bài tập 1.29: Đồ thị của các hàm số y = sin x và y = cos x cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn ?

A. 5

B. 6

C. 4

D. 7

Giải nhanh:

A. 5

Bài tập 1.30: Tập xác định của hàm số y= là

A. ℝ \ {k2π, k ∈ ℤ}.

B. R\{π/2+k2π,k∈Z}

C. R\{π/2+kπ,k∈Z}

D. ℝ \ {kπ, k ∈ ℤ}

Giải nhanh:

B. R\{π/2+k2π,k∈Z}

B - TỰ LUẬN

Bài tập 1.31: Cho góc α thỏa mãn , cos = Tính giá trị của các biểu thức sau:

a)

b)

c)

d)

Giải nhanh:

Ta có nên . Mặt khác suy ra

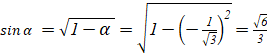
a)

b)

c)

d)

Bài tập 1.32: Cho góc bất kì α. Chứng minh các đẳng thức sau:

a) (sin α + cos α)²= 1 + sin2α

b) cos⁴α–sin⁴α=cos2α

Giải nhanh:

a)  

b)

Bài tập 1.33: Tìm tập giá trị của các hàm số sau:

a) y =2. -1

b) y = sinx + cosx

Giải nhanh:

a)

.

b)

Khi đó ta có hàm số

Lại có:

Bài tập 1.34: Giải các phương trình sau:

a)

b)

c)

Giải nhanh:

a) .

b)

c)  

Bài tập 1.35: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm thu/huyết áp tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số

p(t) = 115 + 25sin(160πt),

trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian t tính theo phút.

a) Tìm chu kì của hàm số p(t).

b) Tìm số nhịp tim mỗi phút.

c) Tìm chỉ số huyết áp. So sánh huyết áp của người này với huyết áp bình thường.

Giải nhanh:

a)

b) Thời gian giữa hai lần tim đập là: (phút).

Số nhịp tim mỗi phút là: nhịp.

c) Ta có: với mọi .

với mọi .

với mọi

Do đó, chỉ số huyết áp của người này là và chỉ số huyết áp của người này cao hơn mức bình thường.

Bài tập 1.36: Khi một tia sáng truyền từ không khí vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới i liên hệ với góc khúc xạ r bởi Định luật khúc xạ ánh sáng

Ở đây, n1 và n2 tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới i = 50°, hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.

Giải nhanh:

Theo đầu bài ta có: . Thay vào ta được:

(với ).

(TMKĐ).

Mà nên

Như vậy góc khúc xạ