A - TRẮC NGHIỆM

Bài tập 1.23: Biểu diễn các góc lượng giác...

Đáp án:

Đáp án A.

Biểu diễn các góc lượng giác $\alpha =-\frac{5\pi}{6}$; $\beta =\frac{\pi }{3}$; $\gamma =\frac{25\pi }{3}$; $\delta =\frac{17\pi }{6}$ trên cùng một đường tròn lượng giác, nhận thấy hai góc và có điểm biểu diễn trùng nhau.

Bài tập 1.24: Trong các khẳng định sau, khẳng định nào là sai...

Đáp án:

Đáp án B.

Vì $cos(\pi -\alpha )=cos(\alpha )$. Do đó đáp án B sai.

Bài tập 1.25: Trong các khẳng định sau, khẳng định nào là sai...

Đáp án:

Đáp án A. 

Ta có các công thức cộng: cos(a – b) = cosacosb + sinasinb 

Bài tập 1.26: Rút gọn biểu thức M = cos(a + b) cos(a – b) – sin(a + b) sin(a – b), ta được...

Đáp án:

Đáp án C. 

M = cos(a + b) cos(a – b) – sin(a + b) sin(a – b) 

= cos[(a + b) + (a – b)]  

= cos 2a =2a  – 1 = 1 – 2a  

Bài tập 1.27: Khẳng định nào sau đây là sai...

Đáp án:

Đáp án C. 

Hàm số y=cos x: 

y(−x) = cos(−x) = cosx = y
=> Là hàm số chẵn và tuần hoàn với chu kì $2\pi$

Bài tập 1.28: Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn...

Đáp án:

Đáp án C. 

Hàm số y=cot x tuần hoàn với chu kì .

Bài tập 1.29: Đồ thị của các hàm số...

Đáp án:

Đáp án A. 

Phương trình hoàn độ giao điểm của 2 đồ thị hàm số là:

sin x=cos x⇔tan x=1 (do $tanx=\frac{sinsinx}{coscosx}$).

<=> $\frac{\pi }{4}+k\pi$; $k\in Z$

Ta có: $-2\pi \leq \frac{\pi}{4}+k\pi\leq \frac{5\pi}{2} <=> \frac{-9\pi}{4}\leq k\pi\leq \frac{9\pi}{4} <=> -2,25\leq k\leq 2,25$

Mà k$\in $Z nên k$\in ${– 2; – 1; 0; 1; 2}.

Bài tập 1.30: Tập xác định của hàm số...

Đáp án:

Đáp án B. 

Biểu thức có nghĩa khi: sin $x -1\neq 0$<=> $sin x \neq 1$ <=> x \neq \frac{\pi}{2}+k2\pi$, k$\in $Z.

Vậy tập xác định của hàm số đã cho là D=R\ {k$\in $Z}.

B - TỰ LUẬN

Bài tập 1.31: Cho góc $\alpha$ thỏa mãn...

Đáp án:

a) $sin sin(\alpha+\frac{\pi}{6})=sin sin \alpha cos cos \frac{\pi}{6}+cos cos\alpha sin sin \frac{\pi}{6}=\frac{\sqrt{6}}{3}.\frac{\sqrt{3}}{2}+(-\frac{1}{\sqrt{3}}).\frac{1}{2}=\frac{-\sqrt{3}}{6}+\frac{\sqrt{2}}{2}$

b) $cos cos(\alpha+\frac{\pi}{6})=coscos \alpha cos cos \frac{\pi}{6}-sinsin\alpha sin sin \frac{\pi}{6}=(-\frac{1}{\sqrt{3}}).\frac{\sqrt{3}}{2}-\frac{\sqrt{6}}{3}.\frac{1}{2}= \frac{-1}{2}+\frac{\sqrt{6}}{6}$

c) $sin sin(\alpha-\frac{\pi}{3})=sin sin \alpha cos cos \frac{\pi}{3}-cos cos\alpha sin sin \frac{\pi}{3}=\frac{\sqrt{6}}{3}.\frac{1}{2}-(-\frac{1}{\sqrt{3}}).\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{6}-\frac{1}{2}$

d) $cos cos(\alpha-\frac{\pi}{6})=coscos \alpha cos cos \frac{\pi}{6}+sinsin\alpha sin sin \frac{\pi}{6}=(-\frac{1}{\sqrt{3}}).\frac{\sqrt{3}}{2}+\frac{\sqrt{6}}{3}.\frac{1}{2}= \frac{-1}{2}+\frac{\sqrt{6}}{6}$

Bài tập 1.32: Cho góc bất kì $\alpha$. Chứng minh các đẳng thức sau...

Đáp án:

a) Ta có: $cos cos\alpha^{2}=\alpha + \alpha +2sinsin\alpha cos cos \alpha=1+ sinsin2\alpha$ (đpcm).

b) Ta có: $\alpha-\alpha=(\alpha)^{2}-(\alpha)^{2}=(\alpha+\alpha)(\alpha-\alpha)=1.coscos2\alpha=coscos2\alpha$ (đpcm)

Bài tập 1.33: Tìm tập giá trị của các hàm số sau...

Đáp án:

a) Ta có: $-1\leq cos cos(2x-\frac{\pi}{3})\leq 1$ $\forall x\in R$

<=> $2-1\leq cos cos(2x-\frac{\pi}{3})-1\leq 2-1$ $\forall x\in R$

⟺$-3\leq y \leq 1$ $\forall x\in R$

b) Ta có: $\sqrt{2}(\frac{1}{\sqrt{2}}sinsinx+\frac{1}{\sqrt{2}}coscosx)$

<=> $\sqrt{2}(cos cos\frac{\pi}{4}sinsinx+sinsin\frac{\pi}{4}coscosx)=\sqrt{2}(x+\frac{\pi}{4})$

Khi đó ta có hàm số $y=\sqrt{2}sinsin(x+\frac{\pi}{4})$

Lại có: $-1\leq sinsin(x+\frac{\pi}{4})\leq 1$, $\forall x\in R$

<=> $-\sqrt{2}\leq y\leq \sqrt{2}$, $\forall x\in R$

Bài tập 1.34: Giải các phương trình sau...

Đáp án:

a) $coscos(3x-\frac{\pi}{4})=-\frac{\sqrt{2}}{2}$

<=> $coscos(3x-\frac{\pi}{4})=coscos(\frac{3\pi}{4})$

<=> $[3x-\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi$

       $3x-\frac{\pi}{4}=-\frac{3\pi}{4}+k2\pi$ $(k\in Z)$

<=> $x=\frac{\pi}{3}+k\frac{2\pi}{3}$

       $x=-\frac{\pi}{6}+k\frac{2\pi}{3}$ $(k\in Z)$

b) 2x -1+cos 3x =0

⟺-1-2x +cos 3x =0 

⟺cos 3x =cos 2x

⟺ [$3x=2x+k2\pi$  $ 3x=-2x+k2\pi$ $(k\in Z)$ <=> [x=k2$\pi$     $x=k\frac{2\pi}{5}$    $(k\in Z)$

c) $tantan(2x+\frac{\pi}{5})=tantan(x-\frac{\pi}{6})$

<=> $2x+\frac{\pi}{5}=x-\frac{\pi}{6}+k\pi$, $k\in Z$

<=> $x= -\frac{11\pi}{30}+k\pi$, $k\in Z$

Bài tập 1.35: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim...

Đáp án:

a) $T=\frac{2\pi}{160\pi}=\frac{1}{80}$

b) Thời gian giữa hai lần tim đập là: $T=\frac{1}{80}$ (phút).

Số nhịp tim mỗi phút là: 1 : $\frac{1}{80}=80$ (nhịp)

c) Ta có: $-1\leq sin(160\pi) \leq 1$, $\forall t \in R$.

<=> $-25\leq 25sin(160\pi t) \leq 25$,$\forall t \in R$.

<=> $115-25\leq 115+25sin(160\pi t) \leq 25+115$, $\forall t \in R$.

<=>$90\leq p(t) \leq140$, $\forall t \in R$.

Do đó, chỉ số huyết áp của người này là 140/90 và cao hơn mức bình thường.

Bài tập 1.36: Khi một tia sáng truyền từ không khí vào mặt nước thì một phần...

Đáp án:

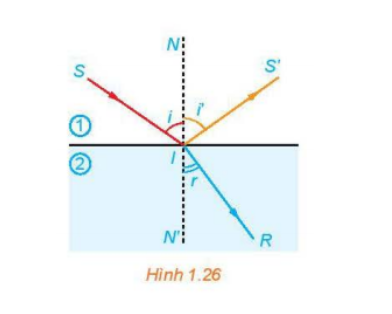
Ta có: $\frac{sinsin50^{\circ}}{sinsinr}=\frac{1,33}{1}$  (với $sinsinr\neq 0$)

<=> ${sinsinr}=\frac{sinsin50^{\circ}}{1,33} \approx 0,57597$ (TMĐK)

<=> $sinsin(35^\circ {10}')$ <=> $r\approx 35^\circ {10}'+k360^{\circ}$ $ r\approx 180 - 35^\circ {10}'+k360^{\circ}$ ($k\in Z$)

<=>  $r\approx 35^\circ {10}'+k360^{\circ}$  $r\approx 144^\circ {50}'+k360^{\circ}$ ($k\in Z$)

Mà $0^{\circ}<r<90^{\circ}$ nên $r\approx 35^\circ {10}'$

Vậy góc khúc xạ  $r\approx 35^\circ {10}'$