1. KHÁI NIỆM PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG

Bài 1: Nhận biết khái niệm hai phương trình tương đương...

Đáp án:

+) $2x-4=0$ ⟺ $x=\frac{4}{2}=2$

Tập nghiệm $S_{1}={2}$.

+) $(x-2)(x^{2}+1)=0$

<=> $[x-2=0$

       $[x^{2}+1>0$

<=> x=2

Tập nghiệm $S_{2}={2}$.

Vậy tập nghiệm của 2 phương trình là tương đương.

Bài 2: Xét sự tương đương của hai phương trình sau...

Đáp án:

+) $\frac{x-1}{x+1}=0 $(ĐKXĐ: x≠-1)

=> $x-1=0$

<=> $x=1$ (thỏa mãn).

Tập nghiệm $S_{1}={1}$.

+) $x^{2}-1=0$

<=> $(x-1)(x+1)=0$

<=> $[x-1=0$

       $[x+1 =0$

<=> $[x=1$

       $[x=-1$

Tập nghiệm $S_{2}={-1;1}$.

Vậy tập nghiệm của 2 phương trình không tương đương

2. PHƯƠNG TRÌNH SINX = M

Bài 1: Nhận biết công thức nghiệm của phương trình...

Đáp án:

a) Hai điểm M, M' lần lượt biểu diễn các góc $\frac{\pi}{6}$ và $-\frac{\pi}{6}=\frac{5\pi}{6}$, lại có tung độ đều bằng $\frac{1}{2}$ nên $sin\frac{\pi}{6}=\frac{1}{2}$ và $sin\frac{5\pi}{6} =\frac{1}{2}$.

Vậy trong nửa khoảng [0;2π), phương trình $sin x =\frac{1}{2}$ có 2 nghiệm là $x=\frac{\pi}{6}$ và $x=\frac{5\pi}{6}$.

b) Vì hàm số sinx tuần hoàn với chu kì là 2 nên ta có công thức nghiệm phương trình là: $x=\frac{\pi}{6}+k2\pi$, k∈Z và $x=\frac{5\pi}{6}+k2\pi$, k∈Z.

Bài 2: Giải các phương trình sau...

Đáp án:

a) $sinsinx=\frac{\sqrt{2}}{2}$

<=>$sinsinx=sinsin\frac{\pi}{4}$

<=>$[x=\frac{\pi}{4}+k2\pi$

      $[x=\pi-\frac{\pi}{4}+k2\pi$

<=>$[x=\frac{\pi}{4}+k2\pi$

      $[x=\frac{3\pi}{4}+k2\pi$ $(k\in Z)$

b) $sinsin3x=-sinsin5x <=> sinsin3x=sinsin(-5x)$

<=> $[3x=-5x+k2\pi$

       $[3x=\pi -(-5x)+k2\pi$ $(k\in Z)$

<=> $[8x=k2\pi$

       $[-2x=\pi+k2\pi$ $(k\in Z)$

<=> $[x=k\frac{\pi}{4}$

       $[x=-\frac{\pi}{2}+k\pi$ $(k\in Z)$

3. PHƯƠNG TRÌNH COSX = M

Bài 1: Nhận biết công thức nghiệm của phương trình...

Đáp án:

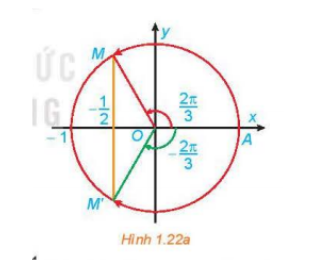
a) Hai điểm M, M' lần lượt biểu diễn các góc $\frac{2\pi}{3}$ và $-\frac{2\pi}{3}$, lại có hoành độ đều bằng $-\frac{1}{2}$ nên $coscos\frac{2\pi}{3} =-\frac{1}{2}$ và $coscos( -\frac{2\pi}{3})=-\frac{1}{2}$.

Vậy trong nửa khoảng $[-\pi;\pi)$ phương trình có hai nghiệm là $x=\frac{2\pi}{3}$và $x=-\frac{2\pi}{3}$.

b) Vì hàm số cos tuần hoàn với chu kì là $2\pi$ nên phương trình đã cho có công thức nghiệm phương trình là:

[ $ x=\frac{2\pi}{3}+k2\pi$ 

$x=-\frac{2\pi}{3}+k2\pi$ , k∈Z. 

Bài 2: Giải các phương trình sau...

Đáp án:

a) $2coscosx =-\sqrt{2}$⟺$coscosx =-\frac{\sqrt{2}}{2}$

⟺$coscosx =coscos\frac{3\pi}{4}$  

⟺ [$x=\frac{3\pi}{4}+k2\pi $               

$x=-\frac{3\pi}{4}+k2\pi$         k∈Z 

b) $coscos3x -sinsin5x =0$

⟺$coscos3x =coscos(\frac{\pi}{2}-5x)$

⟺ [$3x=\frac{\pi}{2}-5x+k2\pi$          $3x=-(\frac{\pi}{2}-5x)+k2\pi$      (k∈Z)

⟺ [$x=\frac{\pi}{16}+k\frac{\pi}{4}$   $x=\frac{\pi}{4}+k\pi$      (k∈Z).

Bài 3: Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được...

Đáp án:

a) F=0 

=> $\frac{1}{2}(1-coscos\alpha ) =0$

⟺$coscos\alpha  =1$⟺$\alpha =k2\pi$, k∈Z 

b) F=0,25

=> $\frac{1}{2}(1-coscos\alpha ) =0,25$

⟺$coscos\alpha =\frac{1}{2}$

⟺$coscos\alpha  =coscos\frac{\pi}{3}$

⟺ [ $\alpha =\frac{2\pi}{3}+k2\pi$     

$\alpha=-\frac{2\pi}{3}+k2\pi$ , (k∈Z).

c) F=0,5 

=> $\frac{1}{2}(1-coscos\alpha ) =0,5$

⟺$coscos\alpha  =0$⟺$\alpha =\frac{\pi}{2}+k\pi$, k∈Z. 

d) F=1

=> $\frac{1}{2}(1-coscos\alpha ) =1$

⟺$coscos\alpha =-1$⟺$\alpha =\pi +k2\pi$, k∈Z. 

4. PHƯƠNG TRÌNH TANX = M

Bài 1: Nhận biết công thức nghiệm của phương trình...

Đáp án:

a) Ta thấy trên khoảng $(-\frac{\pi}{2};\frac{\pi}{2})$, đường thẳng y=1 cắt đồ thị hàm số y=tan x tại điểm có hoành độ $x=\frac{\pi}{4}$

b) Công thức nghiệm của phương trình tan x =1 là: 

$x=\frac{\pi}{4}+k\pi$, k∈Z.

Bài 2: Giải các phương trình sau...

Đáp án:

a) $\sqrt{3}tantan2x =-1$

⟺$tantan 2x =-\frac{1}{\sqrt{3}}$

⟺$tantan 2x =tan(-\frac{\pi}{6})$

⟺$2x=-\frac{\pi}{6}+k\pi$, k∈Z 

⟺$x=-\frac{\pi}{12}+k2\pi$, k∈Z. 

b) $tantan3x +tantan 5x =0$

⟺ $tantan 3x =tantan(-5x)$

⟺$3x=-5x+k\pi$, (k∈Z) 

⟺$x=k\frac{\pi}{8}$, k∈Z .

5. PHƯƠNG TRÌNH COTX = M

Bài 1: Nhận biết công thức nghiệm của phương trình...

Đáp án:

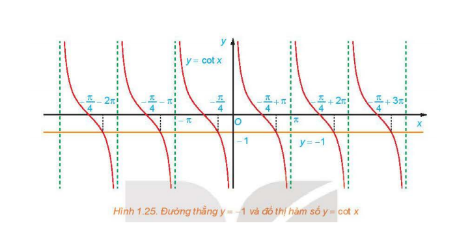
a) Ta thấy trên khoảng $(0;\pi)$, đường thẳng y=-1 cắt đồ thị hàm số y=cot x tại 1 điểm có hoành độ $x=-\frac{\pi}{4}+\pi=\frac{3\pi}{4}$

b) Công thức nghiệm của phương trình cot x =–1 là $x=\frac{3\pi}{4}+k\pi$, k∈Z.

Bài 2: Giải các phương trình sau...

Đáp án:

a) $cotcotx =1$

⟺$cotcotx =cot\frac{\pi}{4}$

⟺$x=\frac{\pi}{4}+k\pi$, k∈Z 

b) $\sqrt{3}cotcotx +1=0$

⟺$cotcotx =-\frac{1}{\sqrt{3}}$

⟺$cotcot x =-\frac{\sqrt{3}}{3}$

⟺$cotcotx =cotcot(-\frac{\pi}{3})$

⟺$x=-\frac{\pi}{3}+k\pi$, k∈Z.

6. SỬ DỤNG MÁY TÍNH CẦM TAY TÌM MỘT GÓC KHI BIẾT GIÁ TRỊ LƯỢNG GIÁC CỦA NÓ

Bài 1: Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết...

Đáp án:

a) Ta bấm phím như sau:

Vậy $\alpha \approx $138°35'26".

Để tìm số đo rađian của góc $\alpha$ , ta bấm phím như sau:

Vậy $\alpha \approx $ 2,41886 rad.

b) Ta bấm phím như sau:

Vậy $\alpha \approx $ 67°52'41".

Để tìm số đo rađian của góc $\alpha$, ta bấm phím như sau:

Vậy $\alpha \approx $1,1847 rad.

c) Ta bấm phím như sau:

Vậy $\alpha \approx $ – 9°11'30".

+ Để tìm số đo rađian của góc $\alpha$, ta bấm phím như sau:

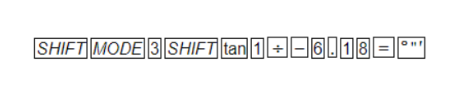
Vậy $\alpha \approx $– 0,16042 rad.

BÀI TẬP CUỐI SGK

Bài tập 1.19: Giải các phương trình sau...

Đáp án:

a) $sinsinx =\frac{\sqrt{3}}{2}$

⟺$sinsinx =sinsin\frac{\pi}{3}$

⟺ [$x=\frac{\pi}{3}+k2\pi$   

$x=\frac{2\pi}{3}+k2\pi$       $k \in Z$.

b) $2coscos x =-\sqrt{2}$

⟺$coscosx=-\frac{\sqrt{2}}{2}$  

⟺$coscosx =coscos\frac{3\pi}{4}$ 

⟺ [$x=\frac{3\pi}{4}+k2\pi$       

$x=-\frac{3\pi}{4}+k2\pi$        $k \in Z$.

c) $\sqrt{3}tantan(\frac{x}{2}+15^{\circ})=1$

<=> $\sqrt{3}tantan(\frac{x}{2}+15^{\circ})=tantan30^{\circ}$

<=> $x=30^{\circ}+k360^{\circ}$, $k\in Z$

d) $cotcot( 2x-1) =cotcot\frac{\pi}{5}$

⟺$2x-1=\frac{\pi}{5}+k\pi$, $k \in Z $

⟺$x=\frac{\pi}{10}+\frac{1}{2}+k2\pi$, $k \in Z$. 

Bài tập 1.20: Giải các phương trình sau...

Đáp án:

a) $sinsin2x +coscos 4x =0$

⟺$coscos 4x =sinsin (-2x)$ ⟺$coscos 4x =coscos(\frac{\pi}{2}-(-2x))$

⟺$coscos4x =coscos(\frac{\pi}{2}+2x)$

⟺ [$x=\frac{\pi}{4}+k\pi$     

[$x=-\frac{\pi}{12}+k3\frac{\pi}{3}$   k∈Z.

b) $coscos 3x = –coscos 7x$

⇔ $cos 3x = cos(\pi + 7x)$

⟺ [$x=-\frac{\pi}{4}+k2\pi$   

[$x=-\frac{\pi}{10}+k\frac{\pi}{5}$  k∈Z.

Bài tập 1.21: Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban...

Đáp án:

a) $-\frac{49}{2500000\alpha}x^{2}+x.tantan\alpha=0$

<=> $x(-\frac{49}{2500000\alpha}x+tantan\alpha)=0$

<=> [$x=0$    $x=\frac{2500000\alpha.tantan\alpha}{49}$

<=> x=0 (không tm)  $x=\frac{2500000\alpha.sinsin2\alpha}{49}$                 

Vậy tầm xa mà quả đạn đạt tới là $x=\frac{2500000\alpha.sinsin2\alpha}{49}$ (m).

b) Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m thì x=22 000 m.

Khi đó: $\frac{12500000\alpha.sinsin2\alpha}{49}=22000$⟺$sinsin2\alpha=\frac{539}{625}$

⟺ [$\alpha \approx 29^{\circ}47'36''$       $\alpha \approx 60^{\circ}12'23''$

Bài tập 1.22: Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương...

Đáp án:

Vật qua vị trí cân bằng thì x=0, ta có:

$2coscos(5t-\frac{\pi}{6}=0$

⟺$coscos(5t-\frac{\pi}{6}) =0$

⟺$5t-\frac{\pi}{6}=\frac{\pi}{2}+k\pi$, k∈Z 

⟺$t=\frac{2\pi}{15}+k\frac{\pi}{5}$, k∈Z 

Trong khoảng thời gian từ 0 đến 6 giây, tức là t∈[0;6] 

hay $0\leq \frac{2\pi}{15}+\frac{\pi}{5}\leq 6$

⟺$-\frac{2}{3}\leq k\leq \frac{90-2\pi}{3\pi}$

Vì k ∈ Z nên k∈{0; 1; 2; 3; 4; 5; 6; 7; 8}.

Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.