1. ĐỊNH NGHĨA HÀM SỐ LƯỢNG GIÁC

Bài 1: Hoàn thành bảng sau...

Đáp án:

Bài 2: Tìm tập xác định của hàm số...

Đáp án:

Biểu thức $\frac{1}{sinsinx}$ có nghĩa khi sin x ≠0, tức là: x≠kπ k∈Z. 

Vậy tập xác định của hàm số đã cho là R\{k∈Z}

2. HÀM SỐ CHẴN, HÀM SỐ LẺ, HÀM SỐ TUẦN HOÀN

Bài 1: Cho hai hàm số...

Đáp án:

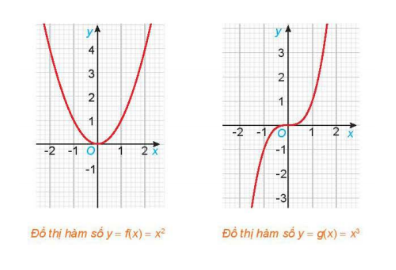
a) Tập xác định của hàm số đã cho là $D_{f}=R$ và $D_{g}=R$

b) ∀x∈$D_{f'}$, ta luôn có: $f(-x)=(-x)^{2}=x^{2}=f(x)$ ∀x∈Df.

=> Đồ thị hàm số $f(x)=x^{2}$ đối xứng với nhau qua trục tung Oy.

c) ∀x∈$D_{g}$, ta luôn có:  $g(-x)=(-x)^{3}=-x^{3}=-g(x)$ ∀x∈Dg.

=> Đồ thị hàm số $g(x)=x^{3}$ đối xứng qua gốc tọa độ O.

Bài 2: Xét tính chẵn, lẻ của hàm...

Đáp án:

Tập xác định của hàm số $g(x)=\frac{1}{x}$ là D=R\{1=0}.

Do đó, nếu x thuộc tập xác định D thì -x cũng thuộc tập xác định D.

Ta có: $g(x)=\frac{1}{-x}=-\frac{1}{x}=-g(x)$, ∀x∈D

Vậy $g(x)=\frac{1}{x}$ là hàm số lẻ.

Bài 3: So sánh...

Đáp án:

a) sin (x+2π) =sinsin[π+(x+π)] =-sinsin (x+π) =-(-sinsin x)=sinsin x , ∀x∈R

b) cos(x+2π) =coscos[π+(x+π)] =-coscos (x+π) =-(-coscos x)=coscosx , ∀x∈R

c) tantan(x+π)=tantan(π+x)=tantanx, x≠$\frac{\pi}{2}$+kπ, k∈Z

d) cotcot(x+π)=cotcot(π+x)=cotcotx, x≠$\frac{\pi}{2}$+kπ, k∈Z

Bài 4: Hàm số hằng...

Đáp án:

Hàm số hằng f(x)=c (c là hằng số) có tập xác định D=R 

Với T là bất kì số dương nào và với ∀x∈D, ta luôn có:

+) x+T∈D và x-T∈D

+) f(x+T)=c=f(x) (vì f(x) là hàm số hằng nên với x thì giá trị đều bằng c.

Vậy hàm số hằng f(x) = c (c là hằng số) là hàm số tuần hoàn với chu kì là một số dương bất kì.

Bài 5: Xét tính tuần hoàn của hàm số...

Đáp án:

Hàm số y=tan 2x có tập xác định là D=R\ {k∈Z}.

Với mọi số thực x, ta có:

+) $x-\frac{\pi}{2}$∈D, $x+\frac{\pi}{2}$∈D

+) $tantan 2(x+\frac{\pi}{2}) =tan 2x+\pi =tantan 2x$

Vậy $y=tantan2x$ là hàm số tuần hoàn 

3. ĐỒ THỊ VÀ TÍNH CHẤT CỦA HÀM SỐ Y = SINX

Bài 1: Cho hàm số y... 

Đáp án:

a) Hàm số $y=f(x)=sinsinx $ (TXĐ là D=R)

Do đó, nếu x∈D thì -x∈D

Ta có: $f(-x)=sinsin(-x) =-sinsin x =-f(x)$, ∀x∈D

Vậy $y=sinsinx$ là hàm số lẻ.

b) 

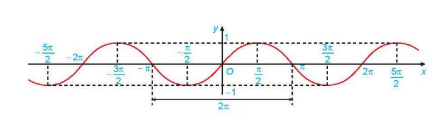
c) Đồ thị của hàm số y = sin x (TXĐ D=R), tập giá trị là [-1;1] 

Đồng biến trên mỗi khoảng $(-\frac{\pi}{2}+k2\pi;\frac{\pi}{2}+k2\pi)$ và nghịch biến trên mỗi khoảng $(\frac{\pi}{2}+k2\pi;\frac{3\pi}{2}+k2\pi)$, $k\in Z$

Bài 2: Tìm tập giá trị của hàm số...

Đáp án:

Ta có: -2≤2sinsinx ≤2 với ∀x∈R.

Vậy hàm số y=2sinsinx có tập giá trị là [-2;2].

Bài 3: Xét tình huống mở đầu...

Đáp án:

a) Thời gian của một chu kì hô hấp đầy đủ là: $T=\frac{2\pi}{\frac{\pi}{3}}=6$ (giây).

Ta có: 1 phút = 60 giây.

Do đó, trong 60s số chu kì hô hấp là $\frac{60}{6}=10$ (chu kì).

b) Ta có: $v=0,85sinsin\frac{\pi t}{3}$

+) v > 0 khi $0,85sinsin\frac{\pi t}{3}>0$⟺$sinsin\frac{\pi t}{3}>0$

Mà -1≤$sinsin\frac{\pi t}{3}$≤1 với ∀x∈R. Do đó, 0<$sinsin\frac{\pi t}{3}$ ≤1.

+) v < 0 khi $0,85sinsin\frac{\pi t}{3}<0$⟺$sinsin\frac{\pi t}{3}<0$

Mà -1<$sinsin\frac{\pi t}{3}$≤1 với ∀x∈R. Do đó, -1≤$sinsin\frac{\pi t}{3}$ <0.

+) Với t∈(0;3) ta có 0<$sinsin\frac{\pi t}{3}$≤1.

+) Với y∈(3;5] ta có -1≤$sinsin\frac{\pi t}{3}$ <0.

Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.

4. ĐỒ THỊ VÀ TÍNH CHẤT CỦA HÀM SỐ Y = COSX

Bài 1: Cho hàm số y = cos x...

Đáp án:

a) Hàm số y=f(x) cos x (TXĐ: D=R)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D.

Ta có: f(-x)=coscos (-x) =coscos x =f(x), ∀x∈D 

Vậy hàm số y=coscos x là hàm số chẵn.

b) 

c) 

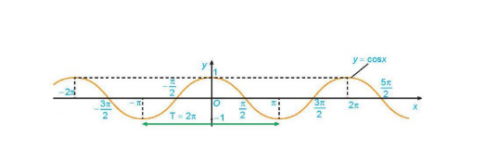
Đồ thị hàm số y=cos x có:

+) Tập giá trị là [–1;1];

+) Đồng biến trên mỗi khoảng:(-π+k2π;k2π), k∈Z 

+) Nghịch biến trên mỗi khoảng: (k2π; π+k2π), k∈Z 

Bài 2: Tìm tập giá trị của hàm số...

Đáp án:

Ta có: $-3≤-3coscos x ≤3$ với mọi x∈R.

Vậy hàm số y=-3cos x có tập giá trị là [-3;3].

Bài 3: Trong Vật lí, ta biết rằng phương trình tổng...

Đáp án:

a) Ta có: $x(t)=-5cos(4πt) = 5cos(4πt + π)$

Ta có thể suy ra: A=5; ωt=4π ; φ =π

b) Thay t = 2 vào phương trình tổng quát, ta được: 

$ωt + \phi  = 4π . 2 + π = 9π$

$T=\frac{2\pi}{\omega }=\frac{2\pi}{4\pi}=\frac{1}{2}$

Số lần vật thực hiện được dao động toàn phần trong 2 giây là $\frac{2}{\frac{1}{2}}=4$

5. ĐỒ THỊ VÀ TÍNH CHẤT CỦA HÀM SỐ Y = TANX

Bài 1: Cho hàm số y = tan x...

Đáp án:

a) Hàm số y = f(x) = tan x, tập xác định là D=R\{k∈Z}.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: $f(-x)=tantan(-x) =-tantan x =-f(x)$, ∀x∈D 

Vậy y=tantan x là hàm số lẻ.

b) 

c) 

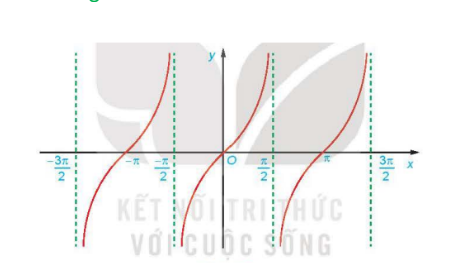
Đồ thị hàm số y = tan x có:

+) Tập giá trị là R.

+) Đồng biến trên mỗi khoảng: ($\frac{\pi}{2}+k\pi$;$\frac{\pi}{2}+k\pi)$, k∈Z 

Bài 2: Sử dụng đồ thị đã vẽ ở Hình 1.16...

Đáp án:

Hàm số y = tan x nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đó ta suy ra trên đoạn $[-\pi;\frac{3\pi}{4}]$ thì y<0 khi $x∈(-\frac{pi}{2};0) \cup (\frac{\pi}{2}; \pi)$

6. ĐỒ THỊ VÀ TÍNH CHẤT CỦA HÀM SỐ Y = COTX

Bài 1: Cho hàm số y = cot x...

Đáp án:

a) Hàm số y = f(x) = cot x, TXĐ là D=R\ {k∈Z}.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: $f(-x)=cotcot(-x) =-cotcot x =-f(x)$, ∀x∈D

Vậy y = cot x là hàm số lẻ

b) 

c) Đồ thị hàm số y=cot x có:

+) Tập giá trị là R;

+) Nghịch biến trên mỗi khoảng:(kπ;π+kπ), k∈Z 

Bài 2: Sử dụng đồ thị đã vẽ ở Hình 1.17...

Đáp án:

Hàm số y=cot x nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đó ta suy ra trên đoạn [-$\frac{\pi}{2};2\pi]$ thì y>0 khi x∈ $(0;\frac{\pi}{2})\cup (\pi;\frac{3\pi}{2})$

BÀI TẬP CUỐI SGK

Bài tập 1.14: Tìm tập xác định của các hàm số sau...

Đáp án:

a) Biểu thức $\frac{1-coscos}{sinsinx}$ có nghĩa khi sinsin x ≠0, tức là x≠k, k∈Z .

Vậy D=R\ {k∈Z}.

b) Biểu thức $\sqrt{\frac{1+coscosx}{2-coscosx}}$ có nghĩa khi { $\frac{1+coscosx}{2-coscosx}≥0$        2-coscos x  ≠0

Vì -1≤coscos x ≤1

Do đó, 2-coscos x ≠0 với mọi x∈R và $\frac{1+coscosx}{2-coscosx} ≥0$ với mọi x∈R.

Vậy D=R.

Bài tập 1.15: Xét tính chẵn lẻ của các hàm số sau...

Đáp án:

a) Biểu thức sinsin 2x +tantan 2x có nghĩa khi coscos 2x ≠0 (do $tantan2x=\frac{sinsin2x}{coscos2x}$) 

=> TXĐ là D=R\ {k∈Z}

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: $f(-x)=sinsin (-2x) +tantan (-2x) =-sinsin 2x -tantan 2x$

                   =$sinsin 2x +tantan 2x =-f(x)$, ∀x∈D.

Vậy y=sin 2x+tan 2x là hàm số lẻ.

b) Tập xác định là D=R.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: $f(–x)= cos (–x)+(-x) =cos x+ (-sinx)^{2} = cos x+x =f(x)$, ∀ x∈D.

Vậy y=cos x+x là hàm số chẵn.

c) Tập xác định là D=R.

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D.

Ta có: f(–x)=sin (–x). cos (–2x)= –sin x.cos 2x= –f(x), ∀x∈D.

Vậy y=sin x cos 2x là hàm số lẻ.

d) Tập xác định là D=R.

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D.

Ta có: f(–x)=sin (–x)+ cos(–x)= –sin x+cos x≠ –f(x);f(-x)≠f(x). ∀x∈D

Vậy y=sin x+cos x là hàm số không chẵn, không lẻ.

Bài tập 1.16: Tìm tập giá trị của các hàm số sau...

Đáp án:

a) Tập xác định của hàm số là D = R

$-1≤sinsin(x-\frac{\pi}{4}) ≤1 $ 

⟺-$2≤2sinsin(x-\frac{\pi}{4}) ≤2$ 

⟺-$2-1≤2sinsin(x-\frac{\pi}{4}) -1<2-1$ 

⟺-$3≤2sinsin(x-\frac{\pi}{4}) -1≤1$

⟺-$3≤y≤1 $

Vậy tập giá trị của hàm số $y=2sinsin(x-\frac{\pi}{4}) -1$ là [-3;1].

b) Tập xác định của hàm số là D = R

Vì $-1≤coscos x ≤1$ với mọi x∈R nên $0≤1+coscos x≤2$  

Do đó, $0\leq \sqrt{1+coscosx}\leq \sqrt{2}$

Suy ra $-2≤\sqrt{1+coscosx}-2≤ \sqrt{2}-2$

Hay $-2≤y≤\sqrt{2}-2$

Vậy tập giá trị của hàm số $y=\sqrt{1+coscosx} -2$ là $[2; \sqrt{2}-2]$

Bài tập 1.17: Từ đồ thị của hàm số y = tan x, hãy tìm các giá trị x sao cho tan x = 0.

Đáp án:

Ta có đồ thị của hàm số y=tan x như hình vẽ dưới đây.

Ta có tan x=0 khi hàm số y = tan x nhận giá trị bằng 0 ứng với các điểm x mà đồ thị giao với trục hoành. 

=> tan x=0 ⬄ x=kπ, k∈Z.

Bài tập 1.18: Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi...

Đáp án:

a) Chu kì của sóng là $T=\frac{2\pi}{\frac{\pi}{10}}=20$ (giây).

b) Giá trị lớn nhất và giá trị nhỏ nhất của hàm số h(t) lần lượt là 90 và -90 nên chiều cao của sóng là 

90 + 90 = 180 (cm).