Dễ hiểu giải Toán 11 kết nối bài 31 Định nghĩa và ý nghĩa của đạo hàm
Giải dễ hiểu Dễ hiểu giải Toán 11 kết nối bài 31 Định nghĩa và ý nghĩa của đạo hàm. Trình bày rất dễ hiểu, nên tiếp thu Toán 11 Kết nối dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
CHƯƠNG IX: ĐẠO HÀM
BÀI 31. ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
1. MỘT SỐ BÀI TOÁN DẪN ĐẾN KHÁI NIỆM ĐẠO HÀM
a) Vận tốc tức thời của một vật chuyển động thẳng
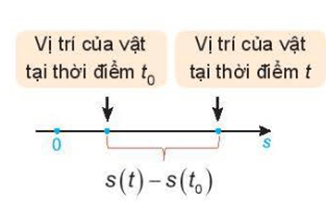
Hoạt động 1 trang 81 sgk Toán 11 tập 2 KNTT: Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).
a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t.
b) Giới hạn ![]() cho ta biết điều gì ?
cho ta biết điều gì ?
Giải nhanh:
a) ![]()
b) Giới hạn ![]() cho ta biết vận tốc tức thời của vật tại thời điểm
cho ta biết vận tốc tức thời của vật tại thời điểm ![]()
b) Cường độ tức thời
Hoạt động 2 trang 82 sgk Toán 11 tập 2 KNTT: Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t)
a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t.
b) Giới hạn ![]() cho ta biết điều gì?
cho ta biết điều gì?
Giải nhanh:
a) ![]() .
.
b) Giới hạn ![]() cho ta biết cường độ tức thời của vật tại thời điểm
cho ta biết cường độ tức thời của vật tại thời điểm ![]()
2. ĐẠO HÀM CỦA HÀM SỐ TẠI MỘT ĐIỂM
Hoạt động 2 trang 45 sgk Toán 11 tập 2 KNTT:
Luyện tập 1 trang 83 sgk Toán 11 tập 2 KNTT: Tính đạo hàm của hàm số tại điểm y = ![]() tại điểm x0 = -1
tại điểm x0 = -1
Giải nhanh:
![]()
![]()
![]()
3. ĐẠO HÀM CỦA HÀM SỐ TRÊN MỘT KHOẢNG
Hoạt động 3 trang 83 sgk Toán 11 tập 2 KNTT: Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau:
a) f(x) = c (c là hằng số);
b) f(x) = x.
Giải nhanh:
![]()
![]()
Luyện tập 2 trang 84 sgk Toán 11 tập 2 KNTT: Tìm đạo hàm của các hàm số sau:
a) y = x2 + 1
b) y = kx + c (với k, c là các hằng số).
Giải nhanh:
a) Với ![]() bất kì, ta có:
bất kì, ta có:
![]()
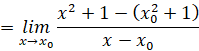
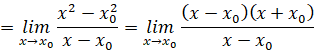
![]()
b) Với ![]() bất kì, ta có:
bất kì, ta có:
![]()
![]()
4. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
Hoạt động 4 trang 84 sgk Toán 11 tập 2 KNTT: Nhận biết tiếp tuyến của đồ thị hàm số
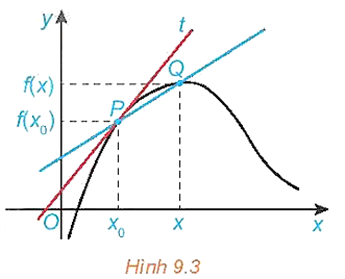
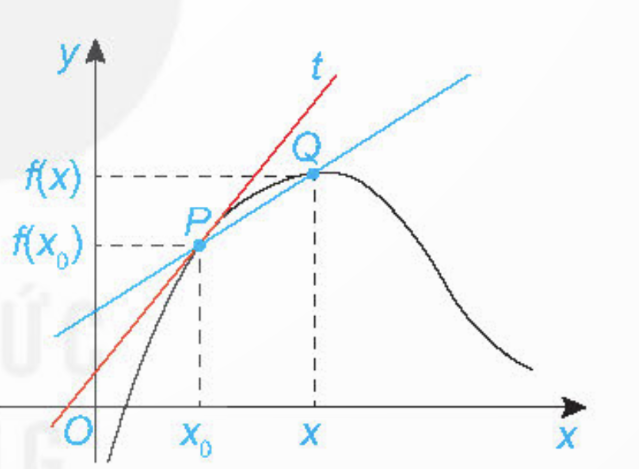
Cho hàm số y = f(x) có đồ thị (C) và P(x0; f(x0)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x0.
a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc kPQ của cát tuyến PQ.
b) Khi x → x0 thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) thay đổi như thế nào?
c) Nếu điểm Q di chuyển trên (C) tới điểm P mà kPQcó giới hạn hữu hạn k thì có nhận xét gì về vị trí giới hạn của cát tuyến QP?
Giải nhanh:
a) ![]()
b) Khi ![]() thì vị trí của điểm
thì vị trí của điểm ![]() trên đồ thị (C) sẽ tiến gần đến điểm
trên đồ thị (C) sẽ tiến gần đến điểm ![]() và khi
và khi ![]() hai điểm này sẽ trùng nhau.
hai điểm này sẽ trùng nhau.
c) Nếu điểm ![]() di chuyển trên
di chuyển trên ![]() tới điểm
tới điểm ![]() mà
mà ![]() có giới hạn hữu hạn
có giới hạn hữu hạn ![]() thì cát tuyến
thì cát tuyến ![]() cũng sẽ tiến đến gần vị trí đường thẳng
cũng sẽ tiến đến gần vị trí đường thẳng ![]()
Luyện tập 3 trang 85 sgk Toán 11 tập 2 KNTT: Tìm hệ số góc của tiếp tuyến của parabol y = x2 tại điểm có hoành độ x0 = 1/2
Giải nhanh:
Ta có ![]() nên
nên ![]() . Vậy hệ số góc của tiếp tuyến của parabol
. Vậy hệ số góc của tiếp tuyến của parabol ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]() là
là ![]() .
.
Hoạt động 5 trang 85 sgk Toán 11 tập 2 KNTT: Cho hàm số y = x2 có đồ thị là đường parabol (P).
a) Tìm hệ số góc của tiếp tuyến của (P) tại điểm có hoành độ x0=1.
b) Viết phương trình tiếp tuyến đó.
Giải nhanh:
a) Ta có ![]() nên
nên ![]() .
.
Vậy hệ số góc của tiếp tuyến của parabol ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]() là
là ![]()
b) ![]()
Luyện tập 4 trang 48 sgk Toán 11 tập 2 KNTT: Viết phương trình tiếp tuyến của parabol (P): y = –2x2 tại điểm có hoành độ x0 = –1.
Giải nhanh:
Ta có: ![]() nên
nên ![]()
Ngoài ra, ![]() nên phương trình tiếp tuyến cần tìm là
nên phương trình tiếp tuyến cần tìm là
![]()
Vận dụng trang 85 sgk Toán 11 tập 2 KNTT: Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m (H.9.4). Độ dốc của mặt cầu không vượt quá 100 (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang như Hình 9.5). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chữ số thập phân thứ nhất).

Giải nhanh:
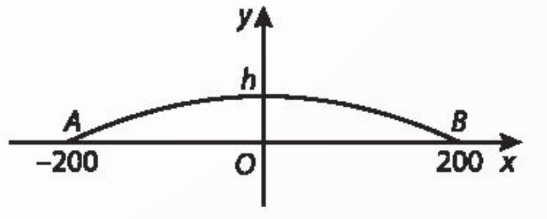
Chọn hệ trục tọa độ Oxy sao cho ![]() là trung điểm
là trung điểm ![]() , tia
, tia ![]() trùng với tia
trùng với tia ![]() , tia Oy hướng lên trên.
, tia Oy hướng lên trên.
Khi đó ![]() . Gọi chiều cao giới hạn của cầu là h
. Gọi chiều cao giới hạn của cầu là h ![]() , suy ra đỉnh cầu có tọa độ
, suy ra đỉnh cầu có tọa độ ![]() .
.
Ta tìm được phương trình parabol của cầu là ![]()
Ta có ![]() .
.
=> ![]() .
.
=> ![]()
Độ dốc của mặt cầu không quá ![]() nên ta có
nên ta có ![]()
Vậy chiều cao giới hạn từ đỉnh cầu tới mặt đường là ![]() .
.
BÀI TẬP
Bài tập 9.1 trang 86 sgk Toán 11 tập 2 KNTT: Tính (bằng định nghĩa) đạo hàm của các hàm số sau:
a) y = x2 – x tại x0 = 1;
b) y = –x3 tại x0 = –1.
Giải nhanh:
a) Ta có: ![]() .
.
Với ![]() .
.
Tính giới hạn ![]() .
.
Vậy ![]() .
.
b) Ta có:
![]() .
.
Với![]() .
.
Tính giới hạn ![]() .
.
Vậy ![]()
Bài tập 9.2 trang 86 sgk Toán 11 tập 2 KNTT: Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
a) y = kx2 + c (với k, c là các hằng số);
b) y = x3.
Giải nhanh:
a) Với ![]() bất kì, ta có:
bất kì, ta có:
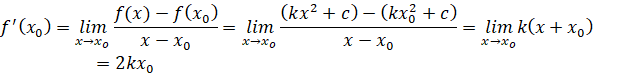
b) Với ![]() bất kì, ta có
bất kì, ta có
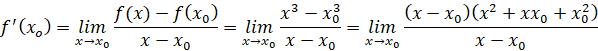
![]()
Bài tập 9.3 trang 86 sgk Toán 11 tập 2 KNTT: Viết phương trình tiếp tuyến của parabol y = –x2 + 4x, biết:
a) Tiếp điểm có hoành độ x0 = 1;
b) Tiếp điểm có tung độ y0 = 0.
Giải nhanh:
Với ![]() bất kì, ta có
bất kì, ta có
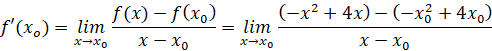
![]()
a) Hệ số góc của tiếp tuyến là ![]() . Ngoài ra, ta có
. Ngoài ra, ta có ![]() nên phương trình tiếp tuyến cần tìm là
nên phương trình tiếp tuyến cần tìm là ![]() hay
hay ![]() .
.
b) Do ![]() nên
nên ![]() . Suy ra
. Suy ra ![]() .
.
Với ![]() , ta có hệ số góc của tiếp tuyến là
, ta có hệ số góc của tiếp tuyến là ![]() , nên phương trình tiếp tuyến cần tìm là
, nên phương trình tiếp tuyến cần tìm là ![]() hay
hay ![]() .
.
Với ![]() , ta có hệ số góc của tiếp tuyến là
, ta có hệ số góc của tiếp tuyến là ![]() , nên phương trình tiếp tuyến cần tìm là
, nên phương trình tiếp tuyến cần tìm là ![]() hay
hay ![]() .
.
Bài tập 9.4 trang 86 sgk Toán 11 tập 2 KNTT: Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t2. Tìm vận tốc của vật khi nó chạm đất.
Giải nhanh:
Khi vật chạm đất thì ![]() , tức là
, tức là ![]()
Ta có : ![]()
![]()
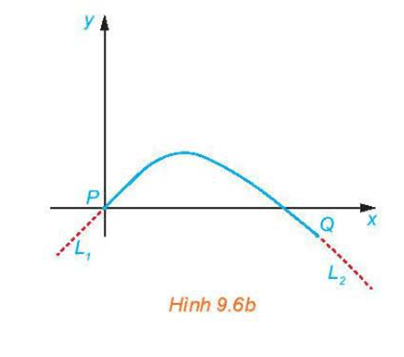
Bài tập 9.5 trang 86 sgk Toán 11 tập 2 KNTT: Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L1 và đoạn dốc xuống L2 là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L1 và L2 phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là y = ax2 + bx + c, trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.

Giải nhanh:
Ta có:
![]() .
.
a) ![]() .
.
b) Ta có ![]() là hệ số góc của đồ thị tại điểm
là hệ số góc của đồ thị tại điểm ![]() ,
, ![]() .
.
=> ![]()
c) Do khoảng cách theo phương ngang giữa ![]() và
và ![]() là
là ![]() nên hoành độ tại điểm
nên hoành độ tại điểm ![]() là 40. Ta có
là 40. Ta có ![]() là hệ số góc của đồ thị tại điểm
là hệ số góc của đồ thị tại điểm ![]() , tức là:
, tức là:
![]()
Do ![]() nên
nên ![]()
Vậy phương trình parabol là ![]()
d) ![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận