CHƯƠNG VII: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN

BÀI 26. KHOẢNG CÁCH

1. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG, ĐẾN MỘT MẶT PHẲNG

Hoạt động 1 trang 54 sgk Toán 11 tập 2 KNTT: a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK ≥ MH (H.7.74).

b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M lên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H7.75).

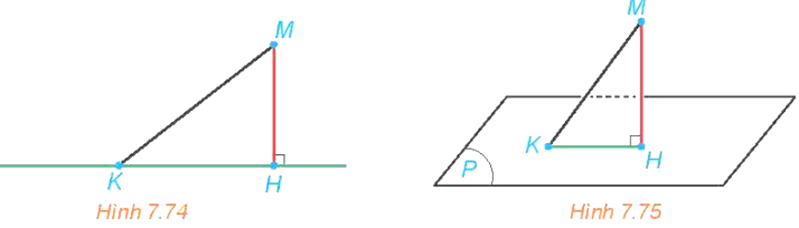
Giải nhanh: 

a) Xét tam giác vuông tại H nên .

Như vậy

b)

Luyện tập 1 trang 55 sgk Toán 11 tập 2 KNTT: Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB=a, AA'= h (H.7.77).

a) Tinh khoảng cách từ A đến mặt phẳng (BCC'B').

b) Tam giác ABC' là tam giác gì? Tính khoảng R cách từ A đến BC'.

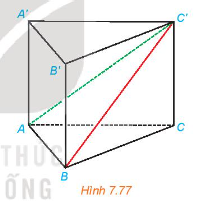
Giải nhanh:

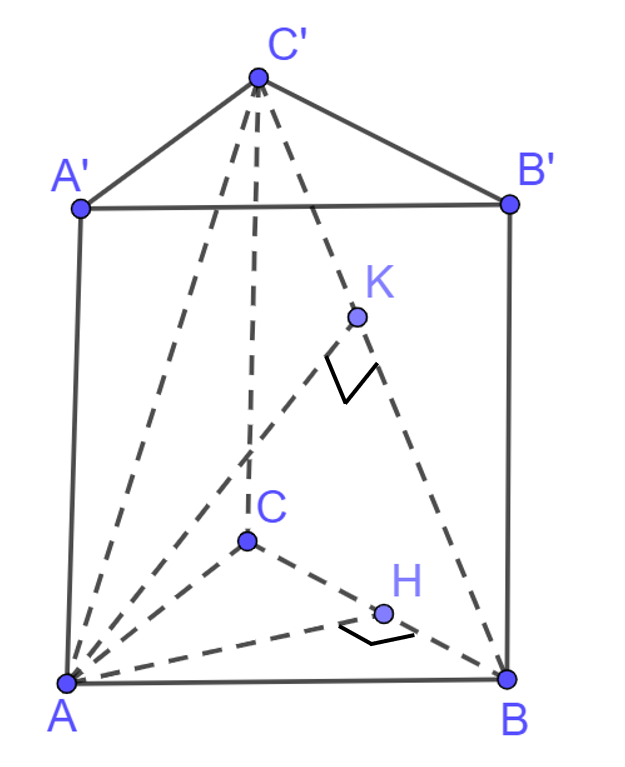
a) Kẻ  tại

b) vuông tại .

Kẻ vuông góc với tại

Ta có:

.

1. KHOẢNG CÁCH GIỮA CÁC ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG, GIỮA HAI MẶT PHẲNG SONG SONG

Hoạt động 2 trang 55 sgk Toán 11 tập 2 KNTT: 

Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M, N bất kì thuộc a và gọi A, B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).

Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).

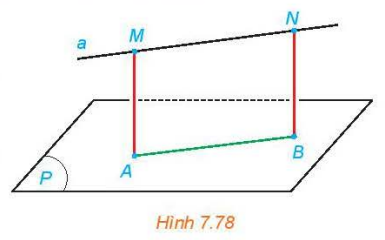
Giải nhanh: 

a) .

b)

Hoạt động 3 trang 56 sgk Toán 11 tập 2 KNTT: a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?

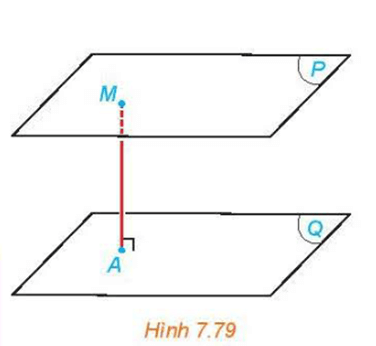
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.

Giải nhanh: 

a) Khi một điểm M thay đổi trên đường thẳng m, khoảng cách từ M đến đường thẳng n không thay đổi 

b) Khi một điểm M thay đổi trên mặt phẳng (P), khoảng cách từ M đến mặt phẳng (Q) không thay đổi. 

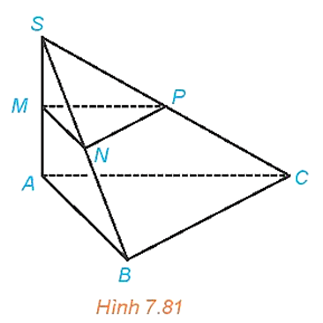
Luyện tập 2 trang 56 sgk Toán 11 tập 2 KNTT: Cho hình chóp S.ABC có SA ⊥⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.

a) Tính d((MNP), (ABC)) và d(NP, (ABC)).

b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A, (SBC)).

Giải nhanh: 

a)

b)

Vận dụng trang 57 sgk Toán 11 tập 2 KNTT: Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 15° so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?

Giải nhanh: 

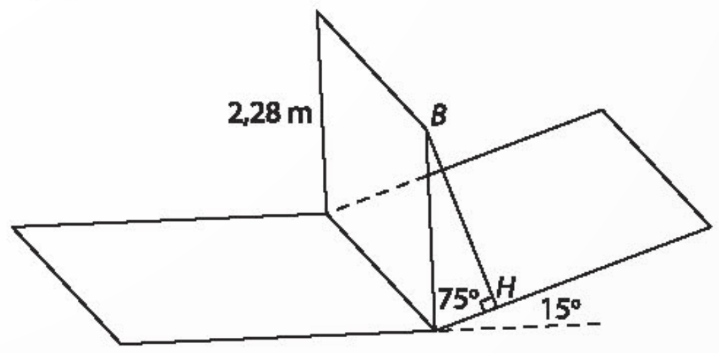
Gọi là một điểm nằm trên thanh ngang và là hình chiếu vuông góc xuống mặt dốc.

 . 

Do đó không cho phép xe cao đi qua.

3. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU 

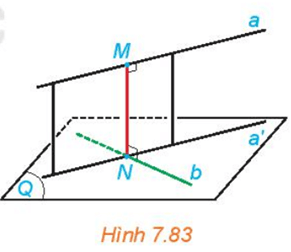
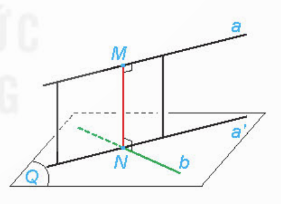
Hoạt động 4 trang 57 sgk Toán 11 tập 2 KNTT: Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).

a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?

b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?

c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.

Giải nhanh: 

a)

b)

c)

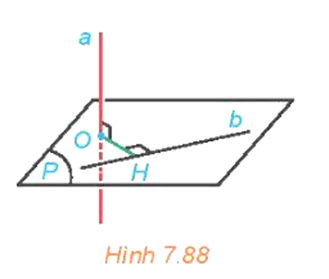
Khám phá trang 58 sgk Toán 11 tập 2 KNTT: Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88). 

Giải nhanh: 

Luyện tập 3 trang 58 sgk Toán 11 tập 2 KNTT: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥⊥ (ABCD), SA = a√22.

a) Tính khoảng cách từ A đến SC.

b) Chứng minh rằng BD ⊥⊥ (SAC).

c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.

Giải nhanh: 

a) .
b) .
c) Kẻ

Lại có

Vậy đường vuông góc chung giữa và là

Thảo luận trang 58 sgk Toán 11 tập 2 KNTT: Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.

Giải nhanh: 

- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.

- Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên mặt phẳng (P).

- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm M bất kì trên a đến mặt phẳng (P).

- Khoảng cách giữa hai mặt phẳng song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

BÀI TẬP

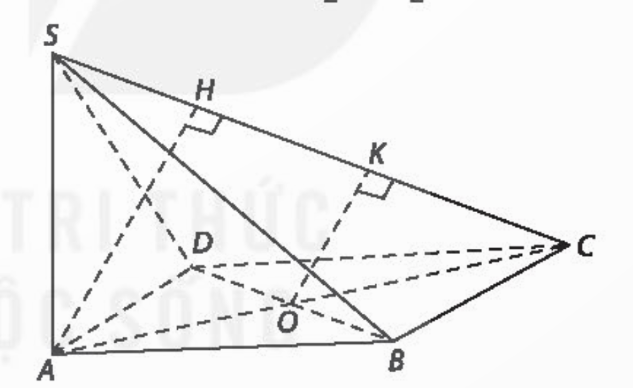
Bài tập 7.22 trang 59 sgk Toán 11 tập 2 KNTT: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) (ABCD)

a) Tính chiều cao của hình chóp.

b) Tính khoảng cách giữa BC và (SAD)

c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD

Giải nhanh: 

a) .
b) .
c) .

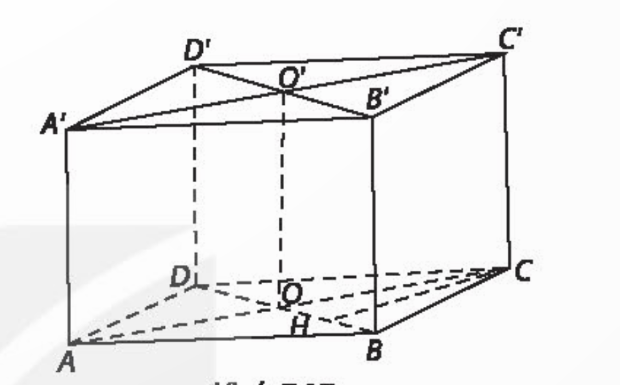
Bài tập 7.23 trang 59 sgk Toán 11 tập 2 KNTT: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.

a) Tính khoảng cách giữa CC' và (BB'D'D).

b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.

Giải nhanh: 

a) .

b) .

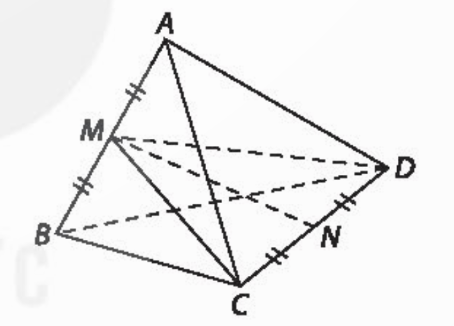
Bài tập 7.24 trang 59 sgk Toán 11 tập 2 KNTT: Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:

a) MN là đường vuông góc chung của AB và CD.

b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.

Giải nhanh: 

a) .

b) . Tương tự cho các cặp còn lại.

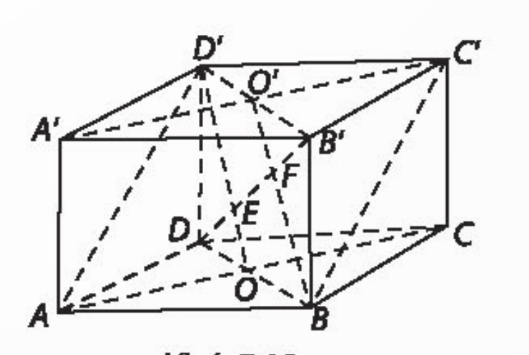
Bài tập 7.25 trang 59 sgk Toán 11 tập 2 KNTT: Cho hình lập phương ABCD.A'B'C'D' có cạnh a.

a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.

b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d(D'AC), (BC'A')).

Giải nhanh: 

a) .

Vì

.

b) .

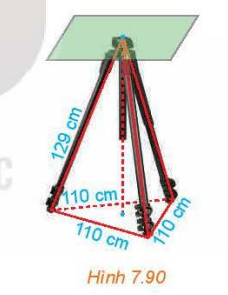
Bài tập 7.26 trang 59 sgk Toán 11 tập 2 KNTT: Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.

Giải nhanh: 

Chiều cao của đáy là:

Khoảng cách từ chân đến tâm là 

Chiều cao giá đỡ là 

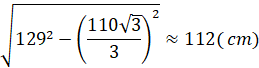
Bài tập 7.27 trang 59 sgk Toán 11 tập 2 KNTT: Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi năm trong bể nước.

Giải nhanh: 

Vì Sợi dây của quả dọi có phương vuông góc với đáy bể và vuông góc với mặt nước.