BÀI TẬP CUỐI CHƯƠNG IV

A.TRẮC NGHIỆM

Bài 4.27: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?

A. =(2;3) và (12;6).                   B. =(;6) và = (1;).

C. (0;1) và (1;0).                       D.(1;3) và (2;-6).

Giải rút gọn:

B

Bài 4.28: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

A. =(2;3) và (4;6).                     B. =(1;-1) và = (-1;).

C. (a;b) và (-b;a).                     D.(1;1) và (2;0).

Giải rút gọn:

C

Bài 4.29: Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?

A. =(1;1)                                                      B. = (1;).

C.=(2;)                                                      D. = ( ).

Giải rút gọn:

D

Bài 4.30 : Góc giữa vectơ  =(-1;1) và  (-2;) có số đo bằng:

A. 90⁰                     B. 0⁰                  C. 135⁰                    D. 45⁰

Giải rút gọn:

C

Bài 4.31:  Khẳng định nào sau đây là đúng?

Giải rút gọn: 

D

Bài 4.32: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

Giải rút gọn: 

B

B.TỰ LUẬN

Bài 4.33: Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.

a. Tìm mối liên hệ giữa hai vectơ và

b. Biểu thị vectơ theo hai vectơ và

Giải rút gọn: 

a. MB = 3MC => ngược hướng với =>

b.

.

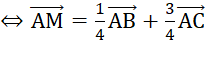Bài 4.34: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

Giải rút gọn:

ABCD là hình bình hành => =>

Bài 4.35: Trong mặt phẳng tọa độ Oxy, cho A(2;1), B(-2; 5) và C(-5; 2).

a. Tìm tọa độ của các vectơ

b. Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó

c. Tìm tọa độ trọng tâm G của tam giác ABC.

d. Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Giải rút gọn: 

a. ; .

b. =>

=> => ΔABC vuông tại B 

      ;  .

c. x_G = ( 2 – 2 - 5 ) : 3 = ; y_G = ( 1 + 5 + 2) : 3 = => G

d.D(x; y) 

   BCAD là hình bình hành ó

     và

     => x – 2 = 3; y – 1 = 3 => x = 5 ; y = 4 => D (5; 4)

Bài 4.36: Trong mặt phẳng tọa độ Oxy cho A(1; 2), B(3; 4), C(-1; -2) và D(6; 5).

a. TÌm tọa độ của các vectơ

b. Hãy giải thích tại sao các vectơ  cùng phương.

c. Giả sử E là điểm có tọa độ (a; 1). Tìm a để các vectơ cùng phương.

d. Với a tìm được, hãy biểu thị vectơ theo các vectơ

Giải rút gọn:

a. ; .

b => cùng phương với  

c. ,

  cùng phương với   => =>

d.

Đặt => = x .2 + y.( -2) ; 1 = x.2 + y. (-4)

 => => .

Bài 4.37: Cho vectơ ≠ . Chứng minh rằng  (hay còn được viết là ) là một vectơ đơn vị, cùng hướng với vectơ

Giải rút gọn:

  có độ dài bằng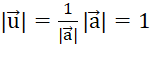

=> là vectơ đơn vị, cùng hướng với .

Bài 4.38: Cho ba vectơ với  = và┴ . Xét một hệ trục Oxy với các vectơ đơn vị Chứng minh rằng:

a. Vectơ có tọa độ là .

b.

Giải rút gọn:

a)

Gọi = (x; y) là tọa độ của vectơ .

=> = .

b) mà   và =>

Bài 4.39 :  Trên sông, một ca nô chuyển động thẳng đều theo hướng S15^oE với vận tốc có độ  bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

Giải rút gọn:

: vận tốc riêng của ca nô, : vận tốc của dòng nước , vận tốc thực tế của ca nô. AC = 20, BC = 3; .

AB² = 20² + 3² – 2.20.3.cos 75⁰ => AB

=> Vận tốc riêng của ca nô  19,44 km/h.