BÀI 26. BIẾN CỐ VÀ ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT

1. BIẾN CỐ

Bài 1: Trở lại Ví dụ 1, xét hai biến cố sau:

A: "Học sinh được gọi là một bạn nữ"';

B: "Học sinh được gọi có tên bắt đầu bằng chữ H".

Hãy liệt kê các kết quả thuận lợi cho biến cố A, B.

Giải rút gọn:

A= {Hương; Hồng; Dung};                 B = { Hoàng; Hương; Hồng}

Bài 2: Phần thưởng trong một chương trình khuyến mãi của một siêu thị là: ti vi, bàn ghế, tủ lạnh, máy tính, bếp từ, bộ bát đĩa. Ông Dũng tham gia chương trình được chọn ngẫu nhiên một mặt hàng. 

a. Mô tả không gian mẫu.

b. Gọi D là biến cố: "ông Dũng chọn được mặt hàng là đồ điện". Hỏi D là tập con nào của không gian mẫu?

Giải rút gọn:

a. = {ti vi; bàn ghế; tủ lạnh; máy tính; bếp từ; bộ bát đĩa}

b. D = {ti vi; tủ lạnh; máy tính; bếp từ}.

Bài 3: Trở lại Ví dụ 1, hãy cho biết, khi nào biến cố C: "Học sinh được gọi là một bạn nam" xảy ra?

Giải rút gọn:

Biến cố C xảy ra khi biến cố A không xảy ra.

Bài 4: Gieo một con xúc xắc. Gọi K là biến cố: "Số chấm xuất hiện trên con xúc xắc là một số nguyên tố".

a. Biến cố: "Số chấm xuất hiện trên con xúc xắc là một hợp số" có là biến cố không?

b. Biến cố K và là tập con nào của không gian mẫu?

Giải rút gọn:

a. Biến cố : "Số chấm xuất hiện trên con xúc xắc là 1 hoặc là một hợp số".

=> Biến cố: "Số chấm xuất hiện trên con xúc xắc là một hợp số" không là  

b.  K = {2; 3; 5};    = {1; 4; 6}.

2. ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT

Bài 1: Một hộp chứa 12 tấm thẻ được đánh số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12. Rút ngẫu nhiên từ hộp đó một tấm thẻ.

a. Mô tả không gian mẫu Ω. Các kết quả có thể có đồng khả năng không?

b. Xét biến cố E: "Rút được thẻ ghi số nguyên tố". Biến cố E là tập con nào của không gian mẫu?

c. Phép thử có bao nhiêu kết quả có thể? Biến cố E có bao nhiêu kết quả thuận lợi? Từ đó, hãy tính xác suất của biến cố E.

Giải rút gọn: 

a. = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.Các kết quả có thể đồng khả năng.

b. E = {2; 3; 5; 7; 11}

c. Phép thử có 12 kết quả có thể.Biến cố E có 5 kết quả thuận lợi =>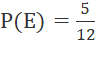

Bài 2: Từ định nghĩa cổ điển của xác suất, hãy chứng minh các nhận xét trên.

Giải rút gọn:

+ ; => .

+ Tập  là biến cố chắc chắn =>

+ Tập  là biến cố không thể ;   => .

Bài 3: Gieo đồng thời hai con xúc xắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 4 hoặc bằng 6.

Giải rút gọn: 

+) E: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 4 hoặc bằng 6”

    Tổng số chấm bằng 4 : (1; 3), (3; 1), (2; 2).

    Tổng số chấm bằng 6: (1; 5), (5; 1), (2; 4), (4; 2), (3; 3)

     ⇒ n(E) = 8.

+) n(Ω) = 6.6 = 36

=> P(E) =

3. NGUYÊN LÍ XÁC SUẤT BÉ

Bài 1: Xác suất của biến cố có ý nghĩa thực tế như sau:

Giả sử biến cố A có xác suất P(A). Khi thực hiện phép thử n lần (n ≥30) thì số lần xuất hiện biến cố A sẽ xấp xỉ bằng n.P(A) (nói chung khi n càng lớn thì sai số tương đối càng bé). Giả thiết rằng xác suất sinh con trai là 0,512 và xác suất sinh con gái là 0,488 . Vận dụng ý nghĩa thực tế của xác suất, hãy ước tính trong số trẻ mới sinh với 10000 bé gái thì có bao nhiêu bé trai.

Hướng dẫn. Gọi n là số trẻ mới sinh. Ta coi mỗi lần sinh là một phép thử và biến cố liên quan đến phép thử là biến cố: "Sinh con gái". Như vậy ta có n phép thử. Ước tính n, từ đó ước tính số bé trai.

Giải rút gọn:

Gọi n là số trẻ mới sinh. 

+) A: "Sinh con gái" => n = 10000: P(A) = 10000 : 0,488 20492

+) B: "Sinh con trai" => n(B) = 20492. 0,512 10492

BÀI TẬP CUỐI SGK

Bài 9.1: Chọn ngẫu nhiên một số nguyên dương không lớn hơn 30.

a. Mô tả không gian mẫu.

b. Gọi A là biến cố: "Số được chọn là số nguyên tố". Các biến cố A và là tập con nào của không gian mẫu?

Giải rút gọn:

a) = { 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30}

b) A = { 2; 3; 5; 7; 11; 13; 17; 19; 23; 29}

     = { 1; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20; 21; 22; 24; 25; 26; 27; 28; 30}

Bài 9.2: Chọn ngẫu nhiên một số nguyên dương không lớn hơn 22 .

a. Mô tả không gian mẫu.

b. Gọi B là biến cố: "Số được chọn chia hết cho 3 ". Các biến cố B và là các tập con nào của không gian mẫu?

Giải rút gọn:

a) = { 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22}

b) B = {3 ; 6; 9; 12; 15; 18; 21}

     = { 1; 2; 4; 5; 7; 8; 10; 11; 13; 14; 16; 17; 19; 20; 22}

Bài 9.3: Gieo đồng thời một con xúc xắc và một đồng xu.

a. Mô tả không gian mẫu.

b. Xét các biến cố sau:

C: "Đồng xu xuất hiện mặt sấp";

D: "Đồng xu xuất hiện mặt ngửa hoặc số chấm xuất hiện trên con xúc xắc là 5".

Các biến cố C,, D và là các tập con nào của không gian mẫu?

Giải rút gọn:

a) = {(1,S) ; ( 1,N); (2,S) ; (2,N); (3,S) ; (3,N); (4,S) ; (4,N); (5,S) ; (5,N); (6,S) ; (6,N) }

b) C = {(1,S) ; (2,S) ; (3,S) ; (4,S) ; (5,S) ; (6,S) }

     = {(1,N) ; (2,N) ; (3,N) ; (4,N) ; (5,N) ; (6,N) }

    D = {(1,N) ; (2,N) ; (3,N) ; (4,N) ; (5,N) ; (5,S) ; (6,N) }

     = {(1,S) ; (2,S) ; (3,S) ; (4,S) ; (6,S) }

Bài 9.4 : Một túi có chứa một số bi xanh, bi đỏ, bi đen và bi trắng. Lấy ngẫu nhiên một viên bi từ trong túi.

a. Gọi H là biến cố: "Bi lấy ra có màu đỏ". Biến cố: "Bi lấy ra có màu xanh hoặc màu đen hoặc trắng" có phải là biến cố hay không?

b. Gọi K là biến cố: "Bi lấy ra có màu xanh hoặc màu trắng". Biến cố: "Bi lấy ra màu đen" có phải là biến cố hay không?

Giải rút gọn:

a) là biến cố: "Bi lấy ra có màu xanh hoặc màu đen hoặc trắng" 

b) : "Bi lấy ra có màu đỏ hoặc màu đen".

   => Biến cố: "Bi lấy ra màu đen" không phải là biến cố .

Bài 9.5 : Hai bạn An và Bình mỗi người gieo một con xúc xắc cân đối. Tính xác suất để:

a. Số chấm xuất hiện trên hai con xúc xắc bé hơn 3 ;

b. Số chấm xuất hiện trên con xúc xắc mà An gieo lớn hơn hoặc bằng 5 ;

c. Tích hai số chấm xuất hiện trên hai con xúc xắc bé hơn 6;

d. Tổng hai số chấm xuất hiện trên hai con xúc xắc là một số nguyên tố. 

Giải rút gọn:

6.6 = 36

a) E = {( 1;1) ; ( 2; 1) ; ( 1; 2) ; ( 2; 2}=> P (E ) =

b) F = { (5; 1) ; ( 5; 2) ; ( 5; 3) ; ( 5; 4) ; ( 5; 5) ; ( 5; 6) ; ( 6; 1) ; ( 6; 2) ; ( 6; 3) ; (6; 4) ; ( 6; 5) ; ( 6; 6) } => P (F) = 

c) G = {( 1;1) ; (1;2) ; (1; 3) ; ( 1; 4) ; ( 1; 5); ( 1; 6) ; ( 2; 1) ; ( 2;2) ; ( 3;1); ( 4; 1) ; ( 5;1)} => P (G) =

d) H ={( 1;1) ; (1; 2) ; (2; 1) ; (1; 4) ; (4; 1) ; (2; 3) ; (3; 2) ; (1; 6); (6; 1) ;(5; 2); ( 2; 5) ; ( 4; 3) ; ( 3; 4); ( 6; 5) ; ( 5; 6)} => P(H) =