BÀI 16.HÀM SỐ BẬC HAI

1. KHÁI NIỆM HÀM SỐ BẬC HAI

Bài 1: Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét (0 < x < 10) là khoảng cách từ điểm cắm cọc đến bờ tường. Hãy tính theo x:

a. Độ dài cạnh PQ của mảnh đất.

b. Diện tích S(x) của mảnh đất được rào chắn.

Giải rút gọn:

a) PQ = 20 – 2x                                            b) S = (20 – 2x) .x = -2x² + 20x

Bài 2: Hàm số nào dưới đây là hàm số bậc hai?

Giải rút gọn:

C

Bài 3: Cho hàm số y = (x -1)(2 - 3x)

a. Hàm số đã cho có phải là hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.

b. Thay dấu ? bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.

Giải rút gọn:

a) y = (x -1)(2-3x) = -3x²+ 5x -2 là hàm số bậc hai có a = -3 ; b = 5; c = -2 

b)

Bài 4:  Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: h = 19,6−4,9t² ; h,t ≥0.

a. Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?

b. Tìm tập xác định và tập giá trị của hàm số h.

Giải rút gọn:

a) 19,6−4,9t² = 0 ⬄ t² = 4⬄ t = 2( giây) ( t ≥ 0)

b) TXĐ : D = ; TGT : [0; 19,6].

2. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI

Bài 1: Xét hàm số y=S(x) = −2x²+20x(0<x<10)

a. Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y=S(x)=−2x²+20x trên khoảng (0;10) như trong hình 6.10. Dạng đồ thị của hàm số y=S(x)=−2x²+20x có giống với đồ thị của hàm số y=S(x)=−2x² hay không?

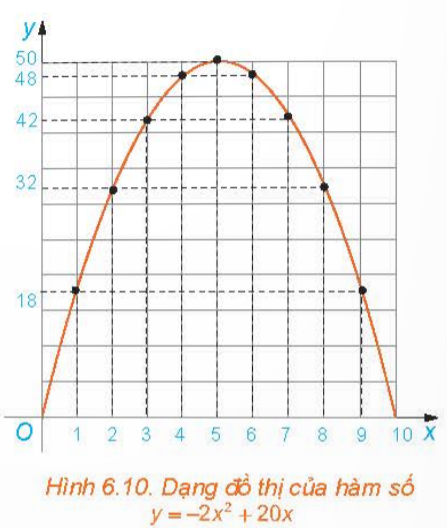
b. Quan sát dạng đồ thị của hàm số y=S(x) = −2x²+20x trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.

c. Thực hiện phép biến đổi
y = −2x²+20x = −2(x²−10x) = −2(x²−2.5.x+25)+50 = −2(x−5)²+50

Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.

Giải rút gọn: 

a) 

Dạng đồ thị của hai hàm số y = S(x) = =2x² + 20x và y = S(x) = =2x² giống nhau.

b) Điểm cao nhất có tọa độ (5; 50)

c) Giá trị lớn nhất của diện tích mảnh đất là 50m² khi hai cột góc rào phải cách bờ tường 5 m.

Bài 2: Tương tự Hoạt động 2, ta có dạng đồ thị của một số hàm số bậc hai sau:

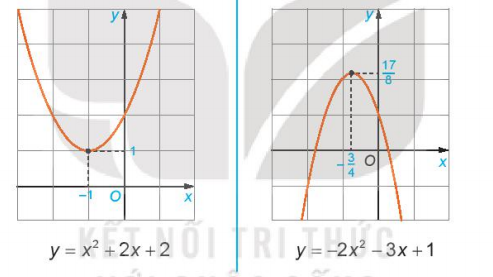
Từ các đồ thị hàm số trên, hãy hoàn thành bảng sau đây:

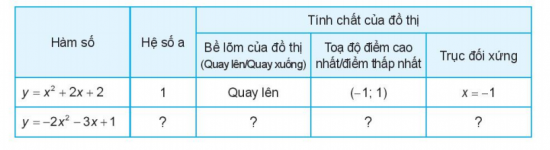
Giải rút gọn:

Bài 3: Vẽ parabol y = 3x²−10x+7. Từ đó tìm khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số y = 3x² −10x+7.

Giải rút gọn: 

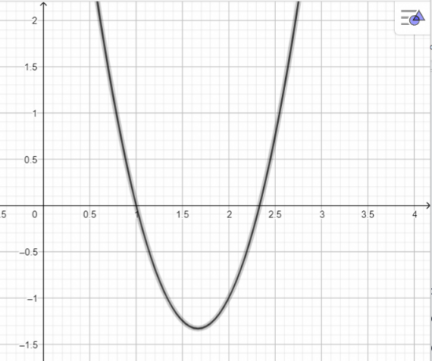
Hàm số nghịch biến trên khoảng ; đồng biến trên khoảng

Giá trị nhỏ nhất là y  tại x .

Bài 4 : Bạn Nam đứng dưới chân cầu vượt ba tầng ở nút giao ngã ba Huế, thuộc thành phố Đà Nẵng để ngắm cầu vượt. Biết rằng trụ tháp dạng đường parabol, khoảng cách giữa hai chân trụ tháp khoảng 27m, chiều cao của trụ tháp tính từ điểm trên mặt đất cách chân trụ tháp 2,26m là 20m. Hãy giúp bạn Nam ước lượng độ cao của đỉnh trụ tháp cầu (so với mặt đất).

Giải rút gọn:

Hàm số dạng (do đồ thị hàm số đi qua O(0; 0)).

Đồ thị hàm số sẽ đi qua điểm (27; 0) và (2,26; 20)

=>

Tọa độ đỉnh là: => độ cao của đỉnh tháp cầu là (m)

BÀI TẬP CUỐI SGK

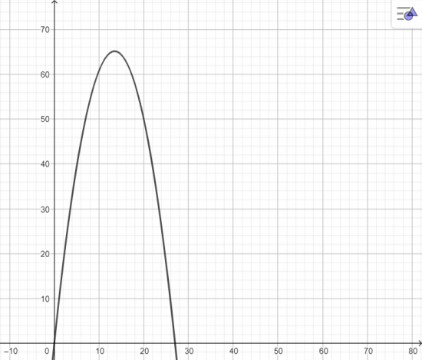
Bài 6.7: Vẽ các đường parabol sau:

Giải rút gọn:

a) 

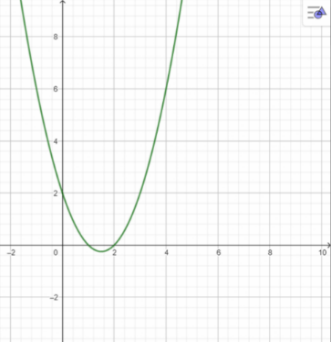
b) 

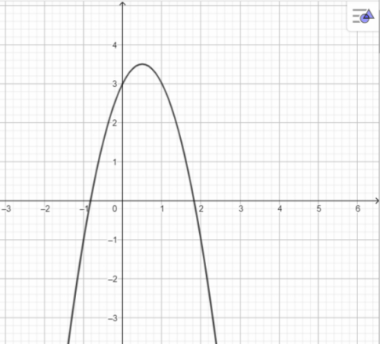
c) 

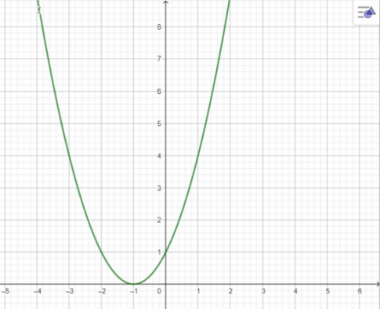
d) 

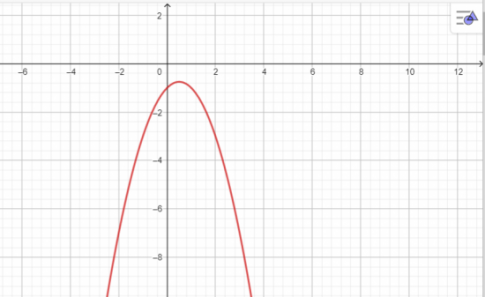
Bài 6.8: Từ các parabol đã vẽ ở Bài tập 6.7 hãy cho biết khoảng đồng biến và khoảng nghịch biến của mỗi hàm số bậc hai tương ứng.

Giải rút gọn:

a) Nghịch biến trên khoảng ; đồng biến trên khoảng .

b) Đồng biến trên khoảng ; nghịch biến trên khoảng

c) Nghịch biến trên khoảng ; đồng biến trên khoảng .

d) Đồng biến trên khoảng ; nghịch biến trên khoảng

Bài 6.9: Xác định parabol y=ax² +bx+1. trong mỗi trường hợp sau:

a. Đi qua hai điểm A(1; 0) và B(2; 4)

b. Đi qua điểm A(1; 0) và có trục đối xứng x =1

c. Có đỉnh I(1; 2)

d. Đi qua điểm A(-1; 1) và có tung độ đỉnh -0,25.

Giải rút gọn:

a)  =>

b) Trục đối xứng

    => .

c) Đỉnh

    => .

d)

=> a = b = 5 => y = 5x² + 5x + 1

Bài 6.10: Xác định parabol y=ax² +bx+c , biết rằng parabol đó đi qua điểm A(8; 0) và có đỉnh là I(6; -12).

Giải rút gọn:

Có đỉnh

=> y = 3x² – 36x + 96

Bài 6.11: Gọi (P) là đồ thị hàm số bậc hai y=ax2+bx+1. Hãy xác định dấu của hệ số a và biệt thức Δ, trong mỗi trường hợp sau:

a. (P) nằm hoàn toàn phía trên trục hoành.

b. (P) nằm hoàn toàn phía dưới trục hoành.

c. (P) cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành.

d. (P) tiếp xúc với trục hoành và nằm phía trên trục hoành.

Giải rút gọn:

a) a >0 ; Δ < 0                                               b) a >0 ; Δ < 0

c) a >0 ; Δ > 0                                               d) a >0 ; Δ = 0

Bài 6.12: Hai bạn An và Bình trao đổi với nhau: An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng là 0,5 m là 2,93 m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12m.Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách Khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé.

Giải rút gọn:

Hàm số dạng (do parabol đi qua gốc tọa độ)

Parabol đi qua các điểm A(8; 0) và B(0,5; 2,93).

=> => Parabol có đỉnh

=> chiều cao của cổng là 4688 : 375 12,5 (m)

=> Kết quả của An không chính xác.

Bài 6.13 : Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau. 

a. Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) của nó.

b. Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.

Giải rút gọn:

a) Chiều dài hình chữ nhật là 40 : 2 – x = 20 – x (m)

    Diện tích mảnh vườn : S = (20 – x) .x = -x² + 20x (m²)

b) -x² + 20x = - (x -10)² + 100 ≤ 100 

    => diện tích lớn nhất là 100 m² khi chiều dài = chiều rộng = 10 m

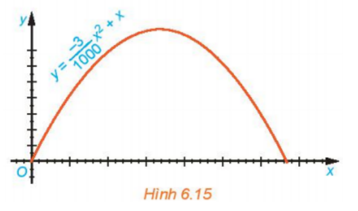
Bài 6.14 : Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình y= x²+x, trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất

a. Tìm độ cao cực đại của vật trong quá trình bay.

b. Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.

Giải rút gọn:

a. Đỉnh I() => độ cao cực đại của vật là : ≈ 83,3 (m) 

b. Điểm chạm đất có tọa độ A(x; 0) ( x > 0)

x² + x = 0  ⬄ x = hoặc x = 0 => x = ( vì x > 0) 

Tầm xa của quỹ đạo là : ≈ 333,3 (m)