CHƯƠNG VI: HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG

BÀI 16. HÀM SỐ BẬC HAI

1. KHÁI NIỆM HÀM SỐ BẬC HAI

HĐ1:

a) PQ = 20 - 2x

b) Diện tích của mảnh đất: S(x)= x.(20-2x)= -2x$^{2}$+20x

Định nghĩa:

Hàm số bậc hai là hàm số cho bởi công thức  y=ax$^{2}$+bx+c,

Trong đó x là biến số, a, b, c là các hằng số và a≠0.

Tập xác định của hàm số bậc hai là  R

Câu hỏi:

Hàm số bậc hai ở ý C.

Nhận xét:

y=ax$^{2}$(a≠0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b=c= 0.

Ví dụ 1 (SGK -tr12)

Luyện tập 1 

a) Ta có: y = (x -1)(2 - 3x) = -3x$^{2}$+5x-3

Hàm số có là hàm bậc hai, hệ số:

a=-3,  b=5,  c=3.

b)

Vận dụng 1:

a) Viên bị chạm đất khi h = 0

Hay 19,6-4,9t$^{2}$=0

⇔4,9t$^{2}$=19,6⇔t$^{2}$=4⇒t=2 (do t≥0.)

Vậy sau 2 giây kể từ khi rơi viên bi chạm đất.

b) Tập xác định: D = [0;+∞)

Ta có: t$^{2}$≥0⇒19,6-4,9t$^{2}$≤19,6

Tập giá trị: [0; 19,6].

2. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI

HĐ2:

a) 

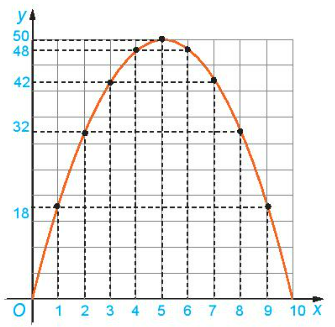
Dạng đồ thị của hàm số y=S(x)=-2x$^{2}$+20x có giống với đồ thị của hàm số y=S(x)=-2x$^{2}$.

b)

Tọa độ điểm cao nhất: (5; 50)

c) Giá trị lớn nhất của y là 50 tại x = 5. 

Suy ra giá trị lớn nhất của diện tích mảnh đất là 50.

Vậy để diện tích mảnh đất lớn nhất thì hai cột góc rào phải cách bờ tường 5 m.

HĐ3: (Bảng ở phía dưới)

Kết luận:

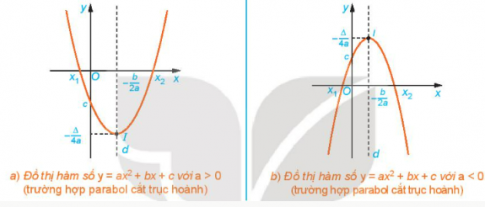
Nhận xét: Đồ thị hàm số bậc hai y=ax$^{2}$+bx+c là một parabol.

Kết luận:

+ Đồ thị hàm số y=ax$^{2}$+bx+c (a≠0) là một đường parabol có đỉnh là điểm I($-\frac{b}{2a}$;$-\frac{\Delta }{4a}$), có trục đối xứng là đường thẳng x=$-\frac{-b}{2a}$. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a <0.

+ Để vẽ đường parabol y=ax$^{2}$+bx+c ta tiến hành các bước sau:

1. Xác định tọa độ đỉnh I($-\frac{b}{2a}$;$-\frac{\Delta }{4a}$);

2. Xác định trục đối xứng x=$-\frac{-b}{2a}$;

3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol.

4. Vẽ parabol.

Ví dụ 2 (SGK -tr15)

Luyện tập 2:

• Tọa độ điểm đỉnh: ($\frac{5}{3}$;$\frac{-4}{3}$)

• Khoảng đồng biến: ($\frac{-4}{3}$;+∞)

• Khoảng nghịch biến: (-∞;$\frac{-4}{3}$)

• Giá trị nhỏ nhất của hàm số là y=$\frac{-4}{3}$  tại x=$\frac{5}{3}$.

Nhận xét: Từ đồ thị hàm số y=ax$^{2}$+bx+c (a≠0), ta suy ra tính chất của hàm số y=ax$^{2}$+bx+c (a≠0):

Vận dụng 2:

Chọn hệ trục tọa độ Oxy sao cho một chân trụ tháp đặt tại gốc tọa độ, chân còn lại đặt trên tia Ox. Khi đó trụ tháp là một phần của đồ thị hàm số dạng y=ax$^{2}$+bx (*) (do đồ thị hàm số đi qua O(0; 0)).

Đồ thị hàm số sẽ đi qua điểm có tọa độ (27; 0) và (2,26; 20), thay tọa độ vào hàm số (*) ta có hệ phương trình:

$\left\{\begin{matrix}0=a.27^{2}+b.27 & \\ 20=a.2,26^{2}+b.2,26 & \end{matrix}\right.$

$\left\{\begin{matrix}a=\frac{-50000}{139781} & \\ b=\frac{1350000}{139781} & \end{matrix}\right.$

Ta có hàm số y=$\frac{-50000}{139781}$x$^{2}$+$\frac{1350000}{139781}$x

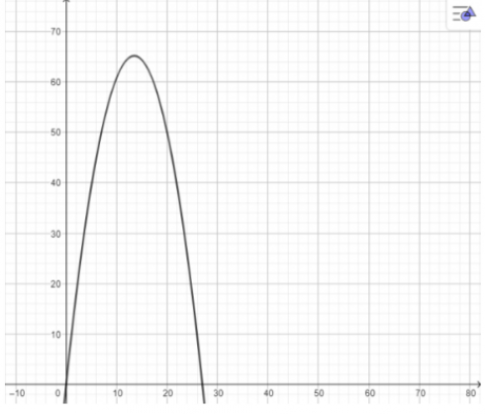
Tọa độ đỉnh của parabol là: (272;$\frac{9112500}{139781}$)

Vậy độ cao của đỉnh trụ tháp cầu là khoảng $\frac{9112500}{139781}$ ≈65,2 mét.