CHƯƠNG 1: PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

BÀI TẬP CUỐI CHƯƠNG I

A – TRẮC NGHIỆM

Bài 1: Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn?

A.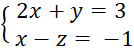

B.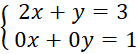

C.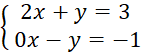

D.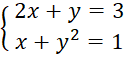

Bài giải chi tiết:

Đáp án đúng là: C

Hệ phương trình A không là hệ hai phương trình bậc nhất hai ẩn vì hệ có 3 ẩn là x, y và z.

Hệ phương trình B không là hệ phương trình bậc nhất hai ẩn vì phương trình thứ hai có cả hai hệ số của hai ẩn x và y đều bằng 0.

Hệ phương trình C là hệ phương trình bậc nhất hai ẩn.

Hệ phương trình D không là hệ hai phương trình bậc nhất hai ẩn vì phương trình thứ hai có bậc 2 với ẩn y.

Bài 2: Nghiệm của hệ phương trình 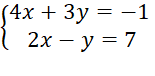là

A. (–1; 1).

B. (3; –1).

C. (;−1)

D. (2; –3)

Bài giải chi tiết:

Đáp án đúng là: D

Ta có: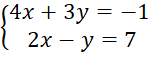

Nhân cả hai vế của phương trình thứ hai với 3 ta được:

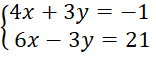
Cộng từng vế của hai phương trình ta được:

10x = 20 hay x = = 2

Thay vào phương trình thứ hai ta được:

2 . 2 – y = 7 hay y = 2 . 2 – 7 = –3.

Vậy hệ phương trình có nghiệm là (2; –3).

Bài 3: Trong mặt phẳng toạ độ Oxy, cho các điểm M(1; 2), N(2; 3), P(–1; –1), Q(5; 8). Đường thẳng 3x – 2y = –1 đi qua hai điểm nào trong các điểm đã cho?

A. M và N.

B. M và P.

C. P và Q.

D. N và P.

Bài giải chi tiết:

Đáp án đúng là: B và C

Ta thấy:

⦁ Thay tọa độ điểm M(1; 2) vào 3x – 2y = –1 , ta được 3 . 1 – 2 . 2 = –1.

Do đó, điểm M nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm N(2; 3) vào 3x – 2y = –1 , ta được 3 . 2 – 2 . 3 = 0 ≠ –1.

Do đó, điểm N không nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm P(–1; –1) vào 3x – 2y = –1 , ta được 3 . (­–1) – 2 . (–1) = –1.

Do đó, điểm P nằm trên đường thẳng d: 3x – 2y = –1.

⦁ Thay tọa độ điểm Q(5; 8) vào 3x – 2y = –1 , ta được 3 . 5 – 2 . 8 = –1.

Do đó, điểm Q nằm trên đường thẳng d: 3x – 2y = –1.

Vậy đường thẳng d: 3x – 2y = –1 đi qua ba điểm M, N, Q.

Bài 4: Giá trị của a và b để đường thẳng y = ax + b đi qua hai điểm (1; –1) và (–1; 5) là

A. a = 1, b = –2.

B. a = –5, b = 1.

C. a = –3, b = 2.

D. a = –1, b = 0.

Bài giải chi tiết:

Đáp án đúng là: C

Đường thẳng y = ax + b đi qua điểm (1; –1) nên ta có:

a . 1 + b = –1 hay a + b = –1

Đường thẳng y = ax + b đi qua điểm (–1; 5) nên ta có:

a . (–1) + b = 5 hay –a + b = 5

Ta được hệ phương trình: 

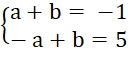
Cộng từng vế của hai phương trình ta được:

2b = 4 hay b = = 2

Thay vào phương trình thứ nhất ta được:

a + 2 = –1 hay a = –1 – 2 = –3.

Vậy với a = –3 và b = 2 thì đường thẳng y = ax + b đi qua hai điểm (1; –1) và (–1; 5)

Bài 5: Hệ phương trình nào sau đây có nghiệm duy nhất?

A.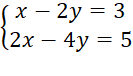

B.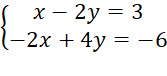

C.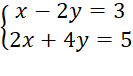

D.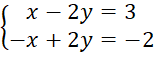

Bài giải chi tiết:

Đáp án đúng là: C

Sử dụng máy tính cầm tay ta được:

⦁ Hệ phương trình A vô nghiệm.

⦁ Hệ phương trình B có vô số nghiệm.

⦁ Hệ phương trình C có nghiệm duy nhất (114;−18)114;−18.

⦁ Hệ phương trình D vô nghiệm

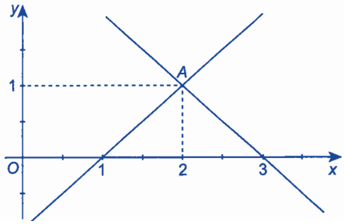
Bài 6: Hình bên dưới minh hoạ tập nghiệm của hệ phương trình nào sau đây?

A.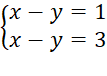

B.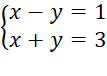

C.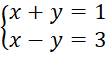

D.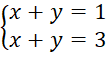

Bài giải chi tiết:

Đáp án đúng là: B

Dễ thấy hai hệ phương trình 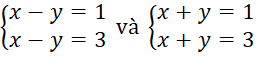vô nghiệm vì trừ từng vế hai phương trình của hệ ta được 0x + 0y = 2.

⦁ Xét hệ phương trình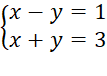

Cộng từng vế hai phương trình ta được: 2x = 4 hay x = = 2

Thay vào phương trình thứ nhất ta được: 2 – y = 1 hay y = 2 – 1 = 1.

Hệ có nghiệm là (2; 1).

⦁ Xét hệ phương trình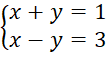

Cộng từng vế hai phương trình ta được: 2x = 4 hay x = = 2

Thay vào phương trình thứ nhất ta được: 2 + y = 1 hay y = 1 – 2 = –1.

Hệ có nghiệm là (2; –1).

Ta thấy giao điểm trên đồ thị có tọa độ là (2; 1). Vậy điểm này là minh họa cho tập nghiệm của hệ phương trình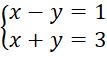

B – TỰ LUẬN

Bài 1.25: Hai nghiệm của phương trình ax + by = 1 là (3; –1) và (–4; –2). Tìm a và b.

Bài giải chi tiết:

(3; –1) là nghiệm của phương trình ax + by = 1 nên ta có:

a . 3 + b . (–1) = 1 hay 3a – b = 1

(–4; –2) là nghiệm của phương trình ax + by = 1 nên ta có:

a . (–4) + b . (–2) = 1 hay –4a – 2b = 1

Ta được hệ phương trình: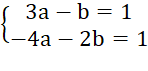

Nhân hai vế của phương trình thứ nhất với 2 ta được: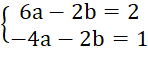

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được

10a = 1 hay a =

Thay vào phương trình thứ nhất ta được:

3 . 0,1 – b = 1 hay 0,3 – b = 1, suy ra b = 0,3 – 1 = –0,7

Vậy với a = 0,1 và b = –0,7 thì hai nghiệm của phương trình ax + by = 1 là (3; –1) và (–4; –2).

Bài 1.26: Giải các hệ phương trình sau:

a)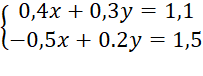

b)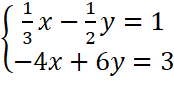

c)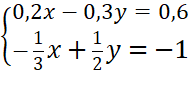

Bài giải chi tiết:

a) Nhân hai vế của phương trình thứ nhất với 5 và nhân hai vế của phương trình thứ hai với 4 ta được:

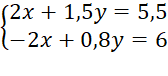
Cộng từng vế hai phương trình ta được:

2,3y = 11,5 hay y = = 5

Thay vào phương trình thứ nhất ta được:

2x + 1,5 . 5 = 5,5 hay 2x + 7,5 = 5,5, suy ra x =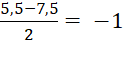

Vậy hệ phương trình có nghiệm là (–1; 5).

b) Nhân hai vế của phương trình thứ nhất với 12 ta được:

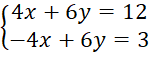
Cộng từng vế hai phương trình ta được:

0x + 0y = 15 (vô nghiệm).

Vậy hệ phương trình không có nghiệm.

c) Nhân hai vế của phương trình thứ nhất với 10 và nhân hai vế của phương trình thứ hai với 6 ta được:

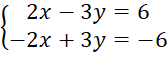
Cộng từng vế hai phương trình ta được:

0x + 0y = 0 (vô số nghiệm).

Xét phương trình 2x – 3y = 6, ta có y = 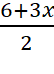= 3 + x

Vậy hệ phương trình có nghiệm (x; 3 + x ) với x∈R tùy ý.

Bài 1.27: Cho hệ phương trình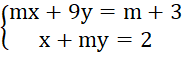

Giải hệ phương trình đã cho trong mỗi trường hợp sau:

a) m = 1;    

b) m = –3;  

c) m = 3

Bài giải chi tiết:

a) Với m = 1 ta có hệ phương trình: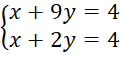

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được

8y = 2 hay y = =

Thay vào phương trình thứ hai ta được:

x + = 2 hay x = 2 - =

Vậy với m = 1 hệ có nghiệm là ( ; )

b) Với m = –3 ta có hệ phương trình: 

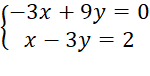
Nhân hai vế của phương trình thứ hai với 3 ta được:

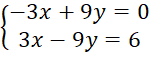
Cộng từng vế của hai phương trình ta được: 0x + 0y = 6 (vô nghiệm).

Vậy với m = 1 hệ phương trình không có nghiệm.

c) Với m = 3 ta có hệ phương trình :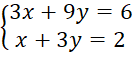 

Nhân hai vế của phương trình thứ hai với 3 ta được:

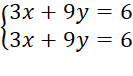
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

0x + 0y = 0 (vô số nghiệm).

Xét phương trình x + 3y = 2, ta có y = = - x

Vậy với m = 3 hệ có nghiệm là (x; - x) với x ∈ R tùy ý.

Bài 1.28: Tìm a để ba đường thẳng sau đồng quy:

d₁: x – y = 1;

d₂: x + y = 3;

d₃: 2x + ay = 1.

Bài giải chi tiết:

Tọa độ giao điểm của hai đường thẳng d₁ và d₂ là nghiệm của hệ phương trình:

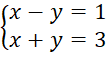
Cộng hai vế của hai phương trình ta được:

2x = 4 hay x = = 2

Thay vào phương trình thứ hai ta được:

2 + y = 3 hay y = 3 – 2 = 1.

Suy ra giao điểm của hai đường thẳng d₁ và d₂ là điểm có tọa độ (2; 1).

Để 3 đường thẳng trên đồng quy thì đường thẳng d₃ cũng phải đi qua điểm (2; 1).

Suy ra 2 . 2 + a . 1 = 1 hay 4 + a = 1, suy ra a = 1 – 4 = –3.

Vậy với a = –3 thì 3 đường thẳng đã cho đồng quy tại điểm có tọa độ (2; 1).

Bài 1.29: Điểm mà tại đó chi phí sản xuất của công ty bằng doanh thu của nó được gọi là điểm hoà vốn. Dưới đây, C thể hiện chi phí sản xuất (tính bằng đô la) của x đơn vị sản phẩm và R thể hiện doanh thu (tính bằng đô la) từ việc bán x đơn vị sản phẩm. Tìm số lượng sản phẩm cần sản xuất và bán đề hoà vốn, nghĩa là tìm giá trị của x để:

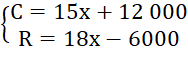
Tính doanh thu của công ty khi đó.

Bài giải chi tiết:

Tại điểm hòa vốn ta có C = R nên hệ phương trình ở đề bài tương đương với:

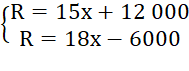hay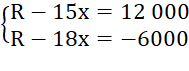

Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

3x =18 000 hay x = 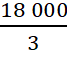= 6000

Thay vào phương trình thứ nhất ta được:

R – 15 . 6 000 = 12 000 hay R = 12 000 + 15 . 6 000 = 102 000.

Vậy doanh thu của công ty khi hòa vốn là 102 000 đô la.

Bài 1.30: Một buổi biểu diễn ca nhạc bán được 1 500 vé. Mỗi vé loại I có giá 250 nghìn đồng và mỗi vé loại II có giá 150 nghìn đồng. Tổng số tiền bán vé thu được là 285 triệu đồng. Hỏi mỗi loại vé đã bán được bao nhiêu vé?

Bài giải chi tiết:

Gọi x, y (vé) lần lượt là số vé loại I và số vé loại II đã bán (x,y∈N*).

Tổng số vé đã bán là 1 500 vé nên ta có: x + y = 1 500.

Tổng số tiền bán vé là 285 triệu đồng nên ta có:

250 000x + 150 000y = 285 000 000 hay 25x + 15y = 28 500.

Ta được hệ phương trình: 

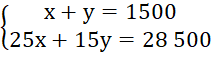
Nhân cả hai vế của phương trình thứ nhất với 15 ta được:

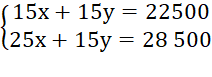
Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất ta được:

10x = 6 000 hay x = 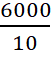= 600

Thay vào phương trình thứ nhất ta được:

600 + y = 1 500 hay y = 1 500 – 600 = 900.

Vậy buổi biểu diễn đã bán được 600 vé loại I và 900 vé loại II.

Bài 1.31: Một khẩu phần súp cà chua chứa 100 calo và 18 gam carbohydrate. Một lát bánh mì nguyên hạt chứa 70 calo và 13 gam carbohydrate, cần bao nhiêu khẩu phần mỗi loại để có được 230 calo và 42 gam carbohydrate?

Bài giải chi tiết:

Gọi x, y lần lượt là số khẩu phần súp cá chua và lát bánh mì để đạt được 230 calo và 42 gam carbohydrate (x,y ∈ N*x).

Lượng calo cần đạt được là 230 calo nên ta có:

100x + 70y = 230 hay 10x + 7y = 23.

Lượng carbohydrate cần đạt được là 42 gam nên ta có:

18x + 13y = 42.

Ta được hệ phương trình: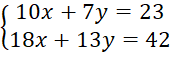

Nhân hai vế của phương trình thứ nhất với 13 và nhân hai vế của phương trình thứ hai với 7 ta được:

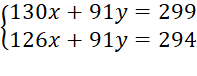
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai ta được:

4x = 5 hay x =

Thay vào phương trình thứ nhất ta được:

10. + 7y = 23 hay + 7y = 23 suy ra y =

Vậy cần khẩu phần súp cà chua và lát bánh mì để có 230 calo và 42 gam carbohydrate.

Bài 1.32: Một loại xe ô tô có mức tiêu hao nhiên liệu là 8,1 lít/100 km khi lái xe trong thành phố và 4,8 lít/100 km khi lái xe trên đường cao tốc. Vào một ngày Chủ nhật, chiếc xe đi tổng quãng đường trong thành phố và trên đường cao tốc là 165 km và tiêu thụ hết 8,415 lít xăng. Tính độ dài quãng đường xe ô tô đi trong thành phố và trên đường cao tốc vào ngày Chủ nhật đó.

Bài giải chi tiết:

Gọi x, y (km) lần lượt là quãng đường ô tô đã đi trong thành phố và trên đường cao tốc (x,y∈N*x).

Tổng quãng đường ô tô đã đi là: x + y = 165 (km).

Lượng xăng ô tô đã tiêu thụ hết là:

8,1x + 4,8y = 8,415 . 100 = 841,5 (lít).

Ta được hệ phương trình: 

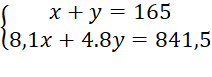
Nhân hai vế của phương trình thứ nhất với 4,8 ta được:

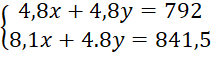
Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất ta được:

3,3x = 49,5 hay x = = 15

Thay vào phương trình thứ nhất, ta được:

15 + y = 165 hay y = 165 – 15 = 150.

Vậy ô tô đã đi 15 km trong thành phố và 150 km trên đường cao tốc