BÀI 21. GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH

Bài tập 6.25 (trang 17): 

Một bức ảnh hình chữ nhật có chiều rộng 8 cm và chiều dài 12 cm. Bức ảnh được phóng to bằng cách tăng chiều dài và chiều rộng thêm một đoạn bằng nhau để tăng gấp đôi diện tích của bức ảnh. Tìm kích thước của bức ảnh mới.

Bài giải chi tiết: 

Diện tích ban đầu của bức ảnh là: 8 . 12 = 96 (cm²)

Gọi độ dài đoạn tăng thêm của mỗi chiều là x (cm) (x > 0).

Diện tích bức ảnh sau khi phóng to là:

(8 + h)(12 + h) = h² + 20h + 96 (cm²)

Diện tích của bức ảnh sau khi phóng to gấp đôi diện tích bức ảnh ban đầu nên ta có:

h² + 20h + 96 = 2 . 96

h² + 20h – 96 = 0

Ta có ∆ = 20² – 4 . 1 . (–96) = 784 > 0 nên phương trình có hai nghiệm phân biệt:

Do đó người ta đã tăng mỗi chiều của bức ảnh thêm 4 cm.

Chiều dài bức ảnh mới là: 12 + 4 = 16 (cm)

Chiều rộng bức ảnh mới là: 8 + 4 = 12 (cm)

Vậy chiều dài và chiều rộng bức ảnh mới lần lượt là 16 cm và 12 cm.

Bài tập 6.26 (trang 17):

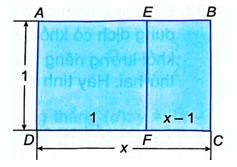
Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng.

a) Tìm tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF.

b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x.

Bài giải chi tiết: 

a) Theo hình vẽ, ta thấy tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật ABCD là:

CDAD=x1=xCDAD=x1=x

Tỉ lệ giữa chiều dài và chiều rộng hình chữ nhật EBCF là:

BCCF=ADCF=1x−1BCCF=ADCF=1x−1

b) Theo đề bài, ta có: x=1x−1x=1x−1

x(x – 1) = 1

x² – x = 1

x² – x – 1 = 0

Ta có: ∆ = (–1)² – 4 . 1 . (–1) = 5 > 0 nên phương trình có hai nghiệm phân biệt:

x1=−(−1)+√52.1=1+√52>0x1=−−1+52.1=1+52>0 (thỏa mãn);

x2=−(−1)−√52.1=1−√52<0x2=−−1−52.1=1−52<0 (không thỏa mãn).

Vậy tỉ lệ vàng là 1+√521+52

Bài tập 6.27 (trang 17): 

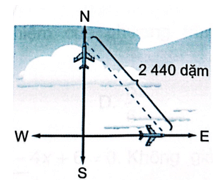
Hai chiếc máy bay khởi hành đồng thời từ một sân bay, một chiếc bay theo hướng bắc và chiếc kia bay theo hướng đông (xem hình bên). Chiếc máy bay đi về hướng bắc đang bay nhanh hơn 50 dặm một giờ so với chiếc máy bay đi về hướng đông. Sau 3 giờ, hai máy bay cách nhau 2 440 dặm. Tìm vận tốc của mỗi máy bay.

Bài giải chi tiết: 

Gọi vận tốc chiếc máy bay đang bay về hướng đông là x (dặm/giờ) (x > 0).

Do đó vận tốc chiếc máy bay đang bay về hướng bắc là x + 50 (dặm/giờ).

Sau 3 giờ hai chiếc máy bay cách nhau 2 440 dặm nên ta có:

(3x)² + [3(x + 50)]² = 2 440²

18x² + 900x – 22 500 = 5 953 600

18x² + 900x – 5 931 100 = 0

9x² + 450x – 2 965 550 = 0

Ta có: ∆ = 450² – 4 . 9 . (–2 965 550) = 106 962 300 > 0 nên phương trình có hai nghiệm phân biệt :

x1=−450+√1069623002⋅9≈549,57>0x1=−450+106  962  3002⋅9≈549,57>0 (thỏa mãn điều kiện)

x2=−450−√1069623002⋅9≈−599,57<0x2=−450−106  962  3002⋅9≈−599,57<0 (không thỏa mãn điều kiện)

Do đó vận tốc của chiếc máy bay đang bay về hướng đông xấp xỉ bằng 549,57 dặm/giờ.

Vận tốc của chiếc máy bay đang bay về hướng bắc xấp xỉ bằng:

549,57 + 50 = 599,57 (dặm/giờ).

Vậy vận tốc của chiếc máy bay đang bay về hướng đông xấp xỉ bằng 549,57 dặm/giờ và vận tốc của chiếc máy bay đang bay về hướng bắc xấp xỉ bằng 599,57 dặm/giờ.

Bài tập 6.28 (trang 17): 

Một phòng họp lúc đầu có một số dãy ghế với tổng cộng 40 chỗ ngồi. Do phải sắp xếp 55 chỗ ngồi cho một cuộc họp nên người ta kê thêm một dãy ghế và mỗi dãy ghế xếp thêm một chỗ ngồi. Hỏi lúc đầu có mấy dãy ghế trong phòng họp đó?

Bài giải chi tiết: 

Gọi số dãy ghế trong phòng họp lúc đầu là x (dãy) (x∈N*x∈ℕ*).

Số chỗ ngồi ở mỗi dãy ghế lúc đầu là 40x40x(chỗ).

Số chỗ ngồi ở mỗi dãy ghế sau khi xếp thêm là 55x+155x+1(chỗ).

Mỗi dãy ghế tăng thêm 1 chỗ ngồi nên ta có phương trình:

55x+1−40x=155x+1−40x=1

55x−40(x+1)(x+1)x=155x−40x+1x+1x=1

55x – 40(x + 1) = x(x + 1)

15x – 40 = x² + x

x² – 14x + 40 = 0

Ta có ∆ = (–14)² – 4 . 1 . 40 = 36 > 0 nên phương trình có hai nghiệm phân biệt:

x1=−(−14)+√362.1=10>0x1=−−14+362.1=10>0(thỏa mãn);

x2=−(−14)−√362.1=4>0x2=−−14−362.1=4>0(thỏa mãn).

Vậy có 2 trường hợp cho phòng họp lúc đầu là có 4 dãy ghế, mỗi dãy có 10 chỗ ngồi và có 10 dãy ghế, mỗi dãy có 4 chỗ ngồi.

Bài tập 6.29 (trang 17): 

Hai anh em Hùng và Nam được mẹ giao nhiệm vụ dọn nhà. Nếu cả hai anh em cùng làm thì mất 225225 giờ để dọn xong nhà. Nếu làm một mình thì tổng 5 cộng thời gian của cả hai anh em để dọn xong là 10 giờ. Hỏi mỗi người cần bao nhiêu thời gian để dọn xong nhà khi làm một mình? (Biết rằng Hùng làm nhanh hơn Nam).

Bài giải chi tiết: 

Đổi 225225giờ = 125125giờ.

Gọi thời gian để Hùng dọn xong nhà khi chỉ làm một mình là x (giờ) (0 < x < 5).

Thời gian Nam cần để dọn xong khi làm một mình là 10 – x (giờ).

Trong 1 giờ Hùng dọn được 1x1x(việc nhà).

Trong 1 giờ Nam dọn được 110−x110−x(việc nhà).

Trong 1 giờ cả Hùng và Nam dọn được 1x+110−x1x+110−x(việc nhà).

Mà hai anh em cùng dọn hết 125125giờ nên mỗi giờ cả hai anh em dọn được:

1:125=5121:125=512 (việc nhà)

Theo đề bài, ta có phương trình:

1x+110−x=5121x+110−x=512

10−x+xx(10−x)=51210−x+xx10−x=512

10x(10−x)=51210x10−x=512

5x(10 – x) = 10 . 12

–5x² + 50x – 120 = 0

x² – 10x + 24 = 0

Ta có: ∆ = (–10)² – 4 . 1 . 24 = 4 > 0 nên phương trình có 2 nghiệm phân biệt:

x1=−(−10)+√42.1=6>5x1=−−10+42.1=6>5 (không thỏa mãn điều kiện);

x2=−(−10)−√42.1=4<5x2=−−10−42.1=4<5 (thỏa mãn điều kiện).

Vậy Hùng cần 4 giờ để dọn xong khi làm một mình và Nam cần 10 – 6 = 6 (giờ) để dọn xong khi làm một mình.

Bài tập 6.30 (trang 17): 

Một cái hộp không có nắp được làm từ mảnh bìa hình chữ nhật có kích thước 30 cm × 40 cm bằng cách cắt ở bốn góc của mảnh bìa bốn hình vuông bằng nhau. Diện tích phần đáy hộp là 336 cm². Tính độ dài mỗi cạnh hình vuông cắt ra ở bốn góc.

Bài giải chi tiết: 

Gọi độ dài cạnh hình vuông là x (cm) (0 < x < 15).

Sau khi cắt thì chiều rộng của hình chữ nhật là 30 – 2x (cm).

Sau khi cắt thì chiều dài của hình chữ nhật là 40 – 2x (cm).

Diện tích phần đáy hộp là (30 – 2x)(40 – 2x) (cm²).

Mà diện tích phần đáy hộp là 336 cm² nên ta có:

(30 – 2x)(40 – 2x) = 336

1200 –140x + 4x² = 336

4x² – 140x + 864 = 0

x² – 35x + 216 = 0

Ta có: ∆ = (–35)² – 4 . 1 . 216 = 361 > 0 nên phương trình có hai nghiệm phân biệt:

x1=−(−35)+√3612.1=27>15x1=−−35+3612.1=27>15(không thỏa mãn điều kiện);

x2=−(−35)−√3612.1=8<15x2=−−35−3612.1=8<15(thỏa mãn điều kiện).

Vậy cạnh của 4 hình vuông cắt ra là 8 cm.

Bài tập 6.31 (trang 18): 

Một người đi xe máy từ tỉnh A đến tỉnh B. Sau đó 16 phút có một ô tô đi từ B về A với vận tốc lớn hơn vận tốc của xe máy là 15 km/h. Xe máy gặp ô tô ở một địa điểm cách B 24 km. Tính vận tốc của ô tô, biết rằng quãng đường AB dài 54 km.

Bài giải chi tiết: 

Đổi 16 phút = 415415giờ.

Gọi vận tốc của xe máy đi từ A đến B là x (km/h) (x > 0).

Vận tốc của ô tô đi từ B về A là x + 15 (km/h).

Hai xe gặp nhau ở địa điểm cách B 24 km nên ô tô đã đi được 24 km.

Quãng đường xe máy đã đi được là: 54 – 24 = 30 (km)

Thời gian ô tô đã đi là 24x+1524x+15giờ.

Thời gian xe máy đã đi là 30x30xgiờ.

Xe máy đi nhiều hơn ô tô 16 phút (415415giờ) nên ta có phương trình:

30x−24x+15=41530x−24x+15=415

30(x+15)−24xx(x+15)=41530x+15−24xxx+15=415

6x+450x(x+15)=4156x+450xx+15=415

15(6x + 450) = 4x(x + 15)

90x + 6 750 = 4x² + 60x

4x² – 30x – 6 750 = 0

2x² – 15x – 3 375 = 0

Ta có: ∆ = (–15)² – 4 . 2 . (–3 375) = 27 225 > 0 nên phương trình có hai nghiệm phân biệt:

x1=−(−15)+√272252.2=45>0x1=−−15+272252.2=45>0 (thỏa mãn điều kiện);

x2=−(−15)−√272252.2=−37,5<0x2=−−15−272252.2=−37,5<0 (không thỏa mãn điều kiện)

Vậy vận tốc của xe máy là 45 km/h và vận tốc của ô tô là 45 + 15 = 60 (km/h).

Bài tập 6.32 (trang 18): 

Khi pha 8 gam chất lỏng thứ nhất với 6 gam chất lỏng thứ hai thì được một dung dịch có khối lượng riêng là 0,7 g/cm. Biết rằng chất lỏng thứ nhất có khối lượng riêng nặng hơn 0,2 g/cm so với khối lượng riêng của chất lỏng thứ hai. Hãy tính khối lượng riêng của mỗi chất lỏng ban đầu.

Bài giải chi tiết: 

Gọi khối lượng riêng của chất lỏng thứ hai là x (g/cm³) (x > 0).

Khối lượng riêng của chất lỏng thứ nhất là x + 0,2 (g/cm³).

Thể tích của chất lỏng thứ nhất là 8x+0,28x+0,2(cm³).

Thể tích của chất lỏng thứ hai là 6x6x(cm³).

Thể tích của hỗn hợp là: 14 : 0,7 = 20 (cm³)

Do đó ta có phương trình:

8x+0,2+6x=208x+0,2+6x=20

8x+6(x+0,2)(x+0,2)x=208x+6x+0,2x+0,2x=20

14x+1,2(x+0,2)x=2014x+1,2x+0,2x=20

14x + 1,2 = 20x(x + 0,2)

14x + 1,2 = 20x² + 4x

20x² – 10x – 1,2 = 0

Ta có ∆ = (–10)² – 4 . 20 . (–1,2) = 196 > 0 nên phương trình có hai nghiệm phân biệt:

x1=−(−10)+√1962.20=0,6>0x1=−−10+1962.20=0,6>0 (thỏa mãn điều kiện);

x2=−(−10)−√1962.20=−0,1<0x2=−−10−1962.20=−0,1<0 (không thỏa mãn điều kiện).

Vậy khối lượng riêng của chất lỏng thứ hai là 0,6 g/cm³ và khối lượng riêng của chất lỏng thứ nhất là 0,6 + 0,2 = 0,8 (g/cm³).