BÀI 18. HÀM SỐ Y=AX2

Bài tập 6.1 (trang 5): 

Thể tích V của hình lăng trụ đứng tứ giác có đáy là hình vuông và chiều cao 5 cm là một hàm số của độ dài cạnh đáy a (cm).

a) Viết công thức của hàm số này và tính độ dài cạnh đáy của hình lăng trụ nếu biết thể tích bằng 180 cm³.

b) Nếu độ dài cạnh a của hình vuông đáy tăng lên hai lần thì thể tích V của khối lăng trụ thay đổi như thế nào?

Bài giải chi tiết: 

a) 

Thể tích hình lăng trụ bằng 180 cm³ nên ta có: 5a² = 180.

Suy ra a² = 36 nên a = 6 (cm).

Vậy độ dài cạnh đáy của hình lăng trụ khi thể tích bằng 180 cm³ là 6 cm.

b) 

Khi độ dài cạnh đáy của hình vuông tăng lên hai lần thì độ dài cạnh đáy khi đó là 2a (cm).

Khi đó thể tích hình lăng trụ là:

V' = S'_đáy . h = (2a)² . h = (2a)² . 5 = 20a² = 4 . 5a² = 4V (cm³)

Vậy khi độ dài cạnh đáy tăng lên 2 lần thì thể tích hình lăng trụ tăng lên 4 lần.

Bài tập 6.2 (trang 6):

Cầu treo Sunshine Skyway bắc qua Vịnh Tampa ở bang Florida (Mỹ), được hỗ trợ bởi 21 dây cáp làm bằng thép, mỗi dây có đường kính 9 inch. Khối lượng mà mỗi dây cáp có thể chịu được là w = 8d² (tấn), trong đó d là đường kính của dây cáp (tính bằng inch) (Theo Algebra 2, NXB McGraw–Hill, 2018).

a) Tính khối lượng tối đa mà cây cầu treo có thể chịu đựng được.

b) Nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì đường kính của dây cáp phải là bao nhiêu?

Bài giải chi tiết: 

a) Khối lượng tối đa mỗi dây cáp đường kính d = 9 inch có thể chịu được là:

8 . 9² = 648 (tấn)

Khối lượng tối đa 21 dây cáp như thế có thể chịu được là:

21 . 648 = 13 608 (tấn)

Vậy khối lượng tối đa cây cầu đó có thể chịu được là 13 608 tấn.

b) Nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì mỗi dây cáp phải chịu được khối lượng tối đa là:

15 162 : 21 = 722 (tấn)

Khi đó ta có: 8d² = 722

Suy ra d2=7228=3614d2=7228=3614.

Do đó d=192=9,5d=192=9,5(inch)

Vậy nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì đường kính của dây cáp phải là 9,5 inch.

Bài tập 6.3 (trang 6): 

Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là F = av² (a là hằng số). Biết rằng khi tốc độ gió bằng 2 m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 120N.

a) Tính hằng số a.

b) Hỏi khi tốc độ gió v = 15 m/s thì lực thổi F của gió bằng bao nhiêu?

c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 12 000 N, hỏi chiếc thuyền có thể đi được trong gió bão với tốc độ gió 90 km/h không?

Bài giải chi tiết: 

a) Khi tốc độ gió bằng 2 m/s thì lực tác động lên cánh buồm là:

F = av² = a . 2² = 4a (N).

Khi đó ta có: 4a = 120 nên a = 30.

Vậy giá trị của hằng số a là 30.

b) Khi tốc độ gió v = 15 m/s thì lực thổi của gió là:

F = 30v² = 30 . 15² = 6 750 (N)

Vậy khi tốc độ gió v = 15 m/s thì lực thổi F của gió bằng 6 750 N.

c) Đổi 90 km/h = 25 m/s.

Trong gió bão với tốc độ gió 90 km/h (25m/s), lực thổi của gió là:

F = 30v² = 30 . 25² = 18 750 (N) > 12 000 N.

Vậy chiếc thuyền không thể đi được trong gió bão với tốc độ gió 90 km/h.

Bài tập 6.4 (trang 6): 

Xác định hệ số a của hàm số y = ax² (a ≠ 0), biết đồ thị của hàm số đi qua điểm:

a) A(−1/2;−3/2);

b) B(1/2;√3/4)

Bài giải chi tiết: 

Bài tập 6.5 (trang 6): 

Trong hình bên có đồ thị của ba hàm số y = –2x², y = x², y = 2x².

a) Cho biết đường nào là đồ thị của hàm số y = –2x².

b) Trong hai đường còn lại, với mỗi x hãy so sánh hai giá trị tương ứng của y để phân biệt đồ thị hai hàm số y = x² và y = 2x².

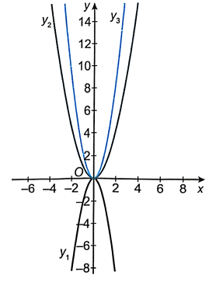
Bài giải chi tiết: 

a) Ta thấy hệ số a của hàm số y = –2x² là –2 < 0 nên đồ thị hàm số nằm dưới trục hoành.

Vậy đồ thị hàm số y = –2x² là đường y₁.

b) Ta có:

Trên đồ thị hàm số y = 2x², với x = 2 thì y = 2 . 2² = 8.^2 222222

Trên đồ thị hàm số y = x², với x = 2 thì y = 2² = 4.^2 222222

Vậy đồ thị hàm số y = 2x² là đường y₃, đồ thị hàm số y = x² là đường y₂.

Bài tập 6.6 (trang 6): 

Trên cùng một mặt phẳng toạ độ Oxy, vẽ và đường thẳng (d): y = x – 2. Dùng đồ thị xác định toạ độ các giao điểm của hai đường này.

Bài giải chi tiết: 

Trên mặt phẳng Oxy, ta vẽ đường thẳng (d): y = x – 2 và parabol (P): y= –x² như hình dưới đây:

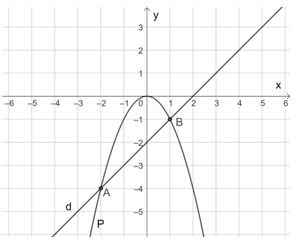
Nhìn vào đồ thị, giao điểm của (d) và (P) là hai điểm A(–2; 4) và B(1; –1).

Bài tập 6.7 (trang 6): 

Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng toạ độ: 

y = 0,75x²; y = –0,75x².

Có nhận xét gì về vị trí của hai đồ thị này so với trục hoành Ox?

Bài giải chi tiết: 

Biểu diễn đồ thị hai hàm số (P₁): y = 0,75x² và (P₂): y = –0,75x² ta được hình vẽ như sau:

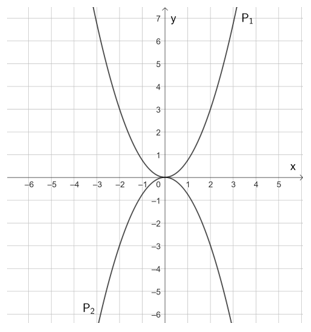
Nhìn vào hình vẽ, ta thấy đồ thị hai hàm số này đối xứng với nhau qua trục hoành.

Bài tập 6.8 (trang 7): 

Cho hàm số y = f(x) = ax² (a ≠ 0).

a) Chứng tỏ rằng nếu (x₀; y₀) là một điểm thuộc đồ thị hàm số thì điểm (–x₀; y₀) cũng nằm trên đồ thị hàm số đó.

b) Chứng minh rằng f(–x) = f(x) với mọi x thuộc ℝ.

Bài giải chi tiết: 

a) Giả sử (x₀; y₀) là một điểm thuộc đồ thị hàm số y = f(x) = ax² (a ≠ 0).

Khi đó ta có: y₀ = ax₀².

Mà y₀ = ax₀² = a(–x₀)² nên điểm (–x₀; y₀) cũng nằm trên đồ thị hàm số đó.

b) Với mọi x thuộc ℝ, ta có:

F(–x) = a(–x)² = ax² = f(x).

Do đó f(–x) = f(x) với mọi x thuộc ℝ. (đpcm)