CHƯƠNG 3 – CĂN BẬC HAI VÀ CĂN BẬC BA

BÀI 7 – CĂN BẬC HAI VÀ CĂN THỨC BẬC HAI

Bài 3.1: Tìm các căn bậc hai của mỗi số sau:

a) 81;

b)

c) 0,0121;

d) 6 400.

Bài giải chi tiết:

Ta thấy:

a) 81 = 9² = (–9)² nên căn bậc hai của 81 là 9 và –9.

b) = ( = 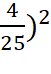nên căn bậc hai của là và

c) 0,0121 = 0,11² = (–0,11)² nên căn bậc hai của 0,0121 là 0,11 và –0,11.

d) 6 400 = 80² = (–80)² nên căn bậc hai của 6 400 là 80 và –80.

Bài 3.2: Sử dụng MTCT tính:

a) (làm tròn kết quả đến chữ số thập phân thứ ba);

b) Các căn bậc hai của 4 021 (làm tròn kết quả đến hàng phần trăm);

c) Giá trị biểu thức 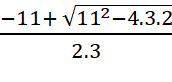(làm tròn kết quả với độ chính xác 0,005).

Bài giải chi tiết:

a) Nhập trên máy tính:

Ta được kết quả ≈ 4,123

b) Nhập trên máy tính:

Ta được kết quả 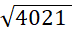≈ 63,41

c) Nhập trên máy tính:

Ta được kết quả 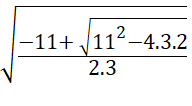≈ −0,19

Bài 3.3: Rút gọn:

a) ( - (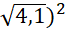

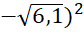
b) ( -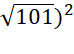

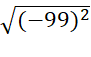
c) – (- + )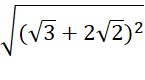

d) -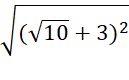

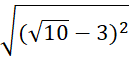
Bài giải chi tiết:

a) ( - (

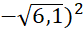
= 4,1 – 6,1 = –2.

b) ( -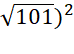

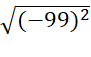
= 101 – 99 = 2.

c) – (- + )

= + ) – (- + )

=

d) √ -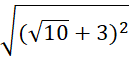

= – (

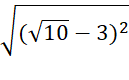
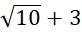= 6

Bài 3.4: Sử dụng các hằng đẳng thức đáng nhớ hiệu hai bình phương và bình phương của một hiệu, rút gọn:

a) ( + ). ( - ).

b)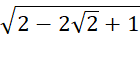

Bài giải chi tiết:

1. ( + ). ( - )

= ( - (

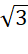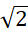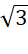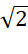= 3 – 2 = 1

b)

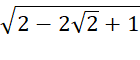
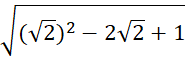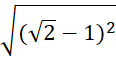= = = | – 1| = – 1

Bài 3.5: Khi giải phương trình ax² + bx + c = 0 (a, b, c là ba số thực đã cho, a ≠ 0), ta phải tính giá trị của căn thức bậc hai 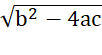. Hãy tính giá trị của căn thức này với các phương trình sau:

a) x² + 5x + 6 = 0;

b) 4x² – 5x – 6 = 0;

c) –3x² – 2x + 33 = 0.

Bài giải chi tiết:

1. Xét phương trình x² + 5x + 6 = 0

Ta có: a = 1, b = 5, c = 6

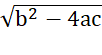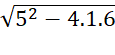= = 1

1. Xét phương trình 4x² – 5x – 6 = 0

Ta có: a = 4, b = –5, c = –6

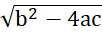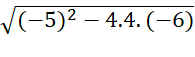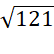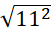= = = = 11

1. Xét phương trình –3x² – 2x + 33 = 0.

Ta có: a = –3, b = –2, c = 33

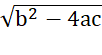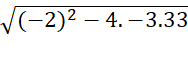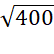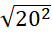= = = = 20

Bài 3.6: Rút gọn các biểu thức sau:

a) 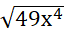- 3x² 

b) 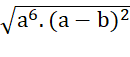: (a-b) với a < b < 0

Bài giải chi tiết:

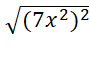1. - 3x² 

= - 3x² 

= 7x² – 3x² = 4x².

Vậy 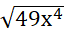- 3x² = 4x².

b) 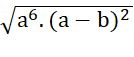: (a - b) với a < b < 0.

= =

=

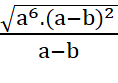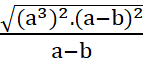
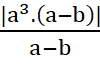
Vì a < b < 0 nên a – b < 0 hay 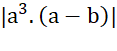= 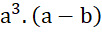suy ra\

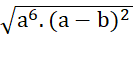: (a - b) = = =

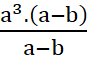Vậy với a < b < 0 thì 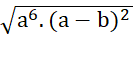: (a - b) =

Bài 3.7: Rút gọn rồi tính giá trị biểu thức:

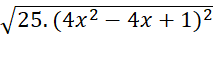tại x =

Bài giải chi tiết:

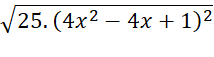
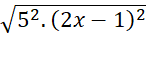= |5(2x - 1)|

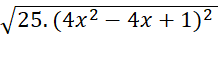Thay x = vào biểu thức ta được:

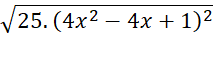
= | 5(2x – 1)| = |5( 2 -1)| = 10 – 5

Vậy với x = thì = 10 – 5