Đáp án Toán 9 Chân trời bài 2: Tứ giác nội tiếp
Đáp án bài 2: Tứ giác nội tiếp. Bài giải được trình bày ngắn gọn, chính xác giúp các em học Toán 9 Chân trời dễ dàng. Từ đó, hiểu bài và vận dụng vào các bài tập khác. Đáp án chuẩn chỉnh, rõ ý, dễ tiếp thu. Kéo xuống dưới để xem chi tiết
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 2. TỨ GIÁC NỘI TIẾP
KHỞI ĐỘNG
Quan sát hai hình tứ giác ABCD và A’B’C’D’, hãy nêu nhận xét sự khác biệt về vị trí các đỉnh của mỗi hình đối với đường tròn trong hình đó.

Đáp án chuẩn:
- Hình a cả bốn điểm A, B, C, D đều nằm trên đường tròn (O).
- Hình b có ba điểm A’, B’, C’ nằm trên đường tròn (O’); điểm D’ nằm ngoài đường tròn.
1. ĐỊNH NGHĨA TỨ GIÁC NỘI TIẾP
HĐ 1. Các tứ giác trong Hình 1 có đặc điểm gì giống nhau?

Đáp án chuẩn:
Đều có các đỉnh nằm trên đường tròn.
Thực hành 1. Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Đáp án chuẩn:


Vận dụng 1. Có nhận xét gì về tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3.
Đáp án chuẩn:
Đều là tứ giác có các đỉnh đều nằm trên đường tròn.
2. TÍNH CHẤT
HĐ 2. Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).
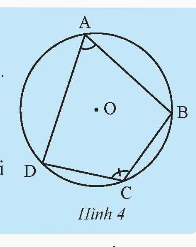
a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp ![]() và
và ![]() .
.
b) Tính tổng số đo của các cung vừa tìm được.
c) Nêu kết luận về tổng số đo của hai góc ![]() và
và ![]() .
.
d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Đáp án chuẩn:
a) - Góc ![]() là góc nội tiếp chắn cung BD nhỏ.
là góc nội tiếp chắn cung BD nhỏ.
- Góc ![]() là góc nội tiếp chắn cung BD lớn.
là góc nội tiếp chắn cung BD lớn.
b) 180o
c) 180o
d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180o
Thực hành 2. Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.

Đáp án chuẩn:
![]() ;
; ![]()
Vận dụng 2. Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết ![]() = 70o,
= 70o, ![]() = 50o. Tìm góc
= 50o. Tìm góc ![]() .
.

Đáp án chuẩn:
![]()
3. ĐƯỜNG TRÒN NGOẠI TIẾP HÌNH CHỮ NHẬT, HÌNH VUÔNG
HĐ 3. Cho hình chữ nhật ABCD và hình vuông MNPQ (Hình 8).

a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD.
b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Đáp án chuẩn:
a) OA, OB, OC, OD bằng nhau
- Nhận xét:
+ Tâm của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo.
+ Đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD là đường chéo của hình chữ nhật.
b) Tâm của đường tròn ngoại tiếp hình vuông MNPQ là I; R ![]() .
.
Thực hành 3. Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
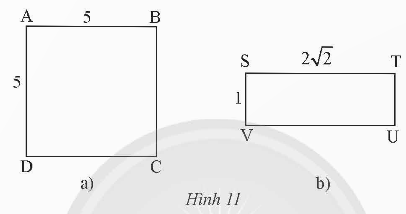
Đáp án chuẩn:

a) tâm M và bán kính R ![]()
b) tâm O và bán kính R = ![]()
Vận dụng 3. Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông
Đáp án chuẩn:
18 (cm2)
4. GIẢI BÀI TẬP CUỐI SÁCH
Bài 1: Cho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở.

Đáp án chuẩn:
Trường hợp Góc | 1 | 2 | 3 | 4 |
| 90o | 70o | 91o | 66o |
| 120o | 80o | 75o | 92o |
| 90o | 80o | 89o | 114o |
| 60o | 70o | 105o | 88o |
Bài 2: Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình
Đáp án chuẩn:

Các tứ giác nội tiếp là AC’HB’, BC’HA, ACB’H, BCB’C’.
Bài 3: Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau:
a) AB = 6 cm, BC = 8 cm; b) AC = 9cm.
Đáp án chuẩn:

a) ![]() cm
cm
b) ![]() cm
cm
Bài 4: Chi hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R.

Đáp án chuẩn:
MP = 2R = QN
![]() = NP = PQ = MQ
= NP = PQ = MQ
Bài 5: Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Đáp án chuẩn:
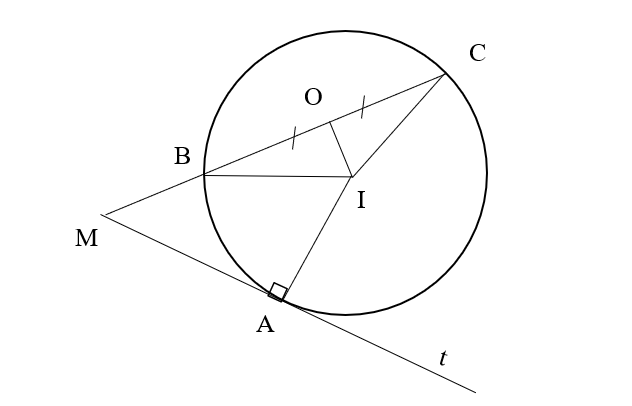
![]()
![]() Tứ giác AMIO là một tứ giác nội tiếp
Tứ giác AMIO là một tứ giác nội tiếp
Bài 6: Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp
b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Đáp án chuẩn:
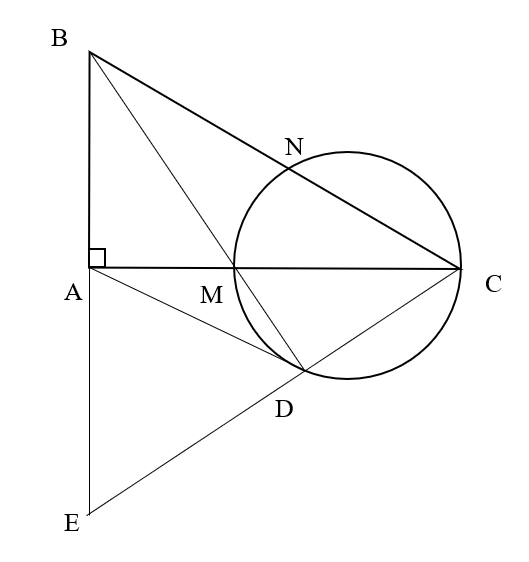
a) ![]() là góc nội tiếp chắn cung BC.
là góc nội tiếp chắn cung BC.
Mà ![]() là góc nội tiếp chắn cung BC (
là góc nội tiếp chắn cung BC (![]() )
) ![]() Tứ giác ABCD nội tiếp.
Tứ giác ABCD nội tiếp.
b) ![]() hay MN
hay MN ![]() NC (1).
NC (1).
M là đường trung trực ![]() EBC
EBC ![]() EM
EM ![]() AC (2).
AC (2).
Từ (1) và (2) ![]() E, M, N thẳng hàng (điều phải chứng minh)
E, M, N thẳng hàng (điều phải chứng minh)
Bài 7: Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N.
a) Chứng minh hai tam giác ABM và ADN bằng nhau.
b) Gọi O là trung điểm MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.
c) Chứng minh ba điểm B, D, O thẳng hàng.
Đáp án chuẩn:
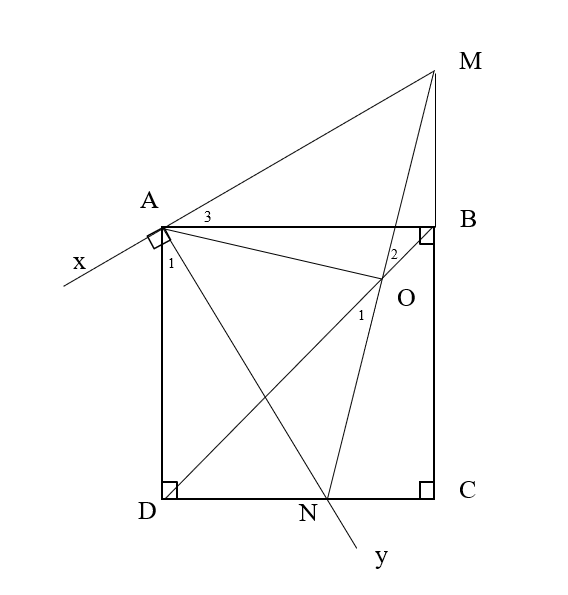
a) Xét ![]() AMB và
AMB và ![]() ADN có: AB = AD ;
ADN có: AB = AD ; ![]() ;
; ![]()
![]()
![]() AMB =
AMB = ![]() ADN (g – c – g)
ADN (g – c – g)
b) Chứng minh ![]() Tứ giác ANDO là một tứ giác nội tiếp
Tứ giác ANDO là một tứ giác nội tiếp
c) Chứng minh ![]() hay ba điểm B, D, O thẳng hàng
hay ba điểm B, D, O thẳng hàng
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận