BÀI 2. TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

1. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG TRÒN

HĐ 1. Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn O trong mỗi hình sau: 

Đáp án chuẩn:

a) Đường thẳng a không tiếp xúc vớid dường tròn (O)

b) Đưởng thẳng a cắt đường tròn (O) tại 1 điểm

c) Đường thẳng a cắt đường tròn (O) tại 2 điểm

Thực hành 1. Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:

a) d = 4 cm;

b) d = 5 cm;

c) d = 6 cm.

Đáp án chuẩn:

a) c cắt (J), c là cát tuyến của đường tròn (J)

b) c là tiếp tuyến của (J)

d) c và (J) không giao nhau

Vận dụng 1. Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.

Đáp án chuẩn:

36 cm

2. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN ĐƯỜNG TRÒN

HĐ 2. Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).

a) Giải thích tại sao ta có OA = R và OM > R.

b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.

Đáp án chuẩn:

a) Vì OM > OA => OM > R

b) Vì đường thẳng d đã được xác định là vuông góc với OA tại điểm A

Thực hành 2. Cho tam giác ABC có đường cao AH. Tìm tiếp tuyển của đường tròn (A; AH). (Hình 8) tại H

Đáp án chuẩn:

CB là tiếp tuyến của đường tròn (A;AH)

Vận dụng 2. Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợ dây là tiếp tuyển của mỗi bánh xe, xác định các tiếp điểm

Đáp án chuẩn:

Các tiếp điểm chính là các điểm của bánh xe đang tiếp xúc trực tiếp với sợi dây

3. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU

HĐ 3. Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).

a) Chứng minh hai tam giác ABO và ACO bằng nhau.

b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.

Đáp án chuẩn:

a) Xét 2 tam giác vuông OAB và OCA có: OB = OC; OA trùng nhau

=> Tam giác OAB = tam giác OCA

b) AB = AC ; OB = OC

=  ; =  ; =

Thực hành 3. Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết EMF = 60^o

a) Tính số đo góc EMI và góc EIF

b) Tính độ dài MI

Đáp án chuẩn:

a)   =  = 30^o

b) MI

Thực hành 4. Tìm giá trị của x trong Hình 12

Đáp án chuẩn:

x = 6

Vận dụng 3. Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.

a) Tính độ dài của hai đoạn dây của MA và MB (kết quả làm tròn đến hàng phần mười).

b) Tính số đo góc tạo bởi hai tiếp tuyến AM, BM và số đo (kết quả làm tròn đến phút).

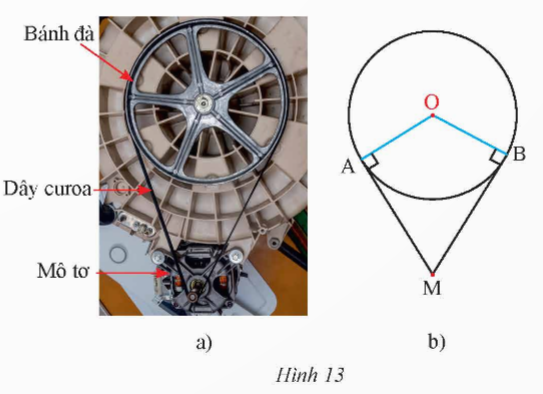
Đáp án chuẩn:

a) MB =

b)    = 50^o44’; = 129^o16’

4. GIẢI BÀI TẬP CUỐI SÁCH

Bài 1: Trong Hình 14, MB, MC lần lượt là tiếp tuyển của đường tròn (O) tại B, C; COB = 130^o. Tính số đo

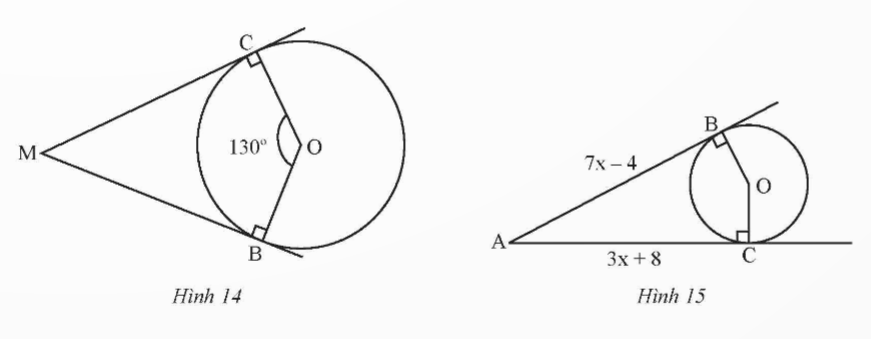
Đáp án chuẩn:

= 50^o

Bài 2: Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x

Đáp án chuẩn:

x = 3

Bài 3: Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O)

Đáp án chuẩn:

Tam giác ABC vuông tại B => AB là tiếp tuyến của đường tròn (O; OB)

Bài 4: Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (HÌnh 17). Tính chu vi tam giác ABC

Đáp án chuẩn:

34 cm

Bài 5: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) ACB có số đo bằng 90°, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của  

c) MC là tiếp tuyến của đường tròn (O; R).

Đáp án chuẩn:

a)

b) Vì I là trung điểm của AC, nên OI là tia phân giác của góc

=> OM cũng là tia phân giác của

c) Ta có  . Vì OI là đường trung tuyến của tam giác AOC => MC là tiếp tuyến của đường tròn (O; R) (đpcm)

Bài 6: Cho đường tròn (O; 5 cm), điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài của MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài của CD.

Đáp án chuẩn:

a) MA = MB = 5 cm

b) cm

Bài 7: Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến (A, B là hai tiếp điểm) thoả mãn AMB = 60°. Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Đáp án chuẩn:

AB = 6 cm

Bài 8: Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B. a) Tính bán kính r của đường tròn (O). b) Tính chiều dài cạnh OA của tam giác ABO.

Đáp án chuẩn:

a) r = 3

b) OA = 5