Đáp án toán 11 Cánh diều bài 1 Dãy số

Đáp án bài 1 Dãy số. Bài giải được trình bày ngắn gọn, chính xác giúp các em học Toán 11 Cánh diều dễ dàng. Từ đó, hiểu bài và vận dụng vào các bài tập khác. Đáp án chuẩn chỉnh, rõ ý, dễ tiếp thu. Kéo xuống dưới để xem chi tiết

Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

CHƯƠNG II. DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN

BÀI 1: DÃY SỐ

I. KHÁI NIỆM

LT-VD 1: Hàm số u(n) = n³ xác định trên tập hợp M = {1;2;3;4;5} là một dãy số hữu hạn. Tìm số hạng đầu, số hạng cuối và viết dãy số trên dưới dạng khai triển

Đáp án chuẩn:

;

Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125

LT-VD 2: Cho dãy số (u_n)=n²

a) Viết năm số hạng đầu và số hạng tổng quát của dãy số (u_n)

b) Viết dạng khai triển của dãy số (u_n)

Đáp án chuẩn:

a) ; với .

II. CÁCH CHO MỘT DÃY SỐ

LT-VD 3: Cho dãy số (u_n) với ... Tìm u₃₃, u₃₃₃ và viết dãy số dưới dạng khai triển

Đáp án chuẩn:

;

III. DÃY SỐ TĂNG, DÃY SỐ GIẢM

LT-VD 4: Chứng minh rằng dãy số (v_n) với v_n=1/3ⁿ là một dãy số giảm

Đáp án chuẩn:

Xét hiệu: =>

Vậy dãy số giảm.

IV. DÃY SỐ BỊ CHẶN

LT-VD 5: Chứng minh rằng dãy số (u_n) với... là bị chặn

Đáp án chuẩn:

=> dãy số bị chặn

BT 1: Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát u_n cho bởi công thức sau:

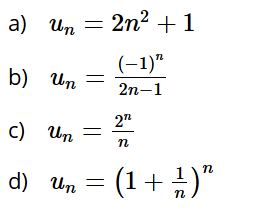
Đáp án chuẩn:

b) ; ; ; ; .

d) .

BT 2:

a) Gọi u_n là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số (un).

b) Gọi v_n là tổng diện tích của các hình tô màu ở hàng thứ n trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số (v_n).

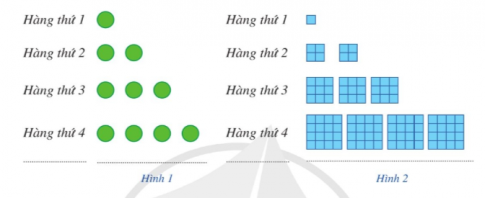
$Gọi $u^{n}$ là số chấm ở hàng thứ $n$ trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số $(u^{n})$.$

Đáp án chuẩn:

BT 3: Xét tính tăng, giảm của mỗi dãy số (u_n), biết:

a) u_n =

c) u_n = (– 1)ⁿ.(2ⁿ + 1).

Đáp án chuẩn:

a) dãy số đa cho là dãy số tăng

b) dãy số đã cho là dãy số giảm

c) với n chẵn thì dãy số đã cho là dãy tăng

BT 4 : Trong các dãy số (u_n) được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?

a) u_n = n² + 2;

b) u_n = – 2n + 1;

Đáp án chuẩn:

a) Dãy số bị chặn dưới bởi 3.

b) Dãy số bị chặn trên bởi

c) Dãy số bị chặn

BT 5: Cho dãy số thực dương (u_n). Chứng minh rằng dãy số (u_n) là dãy số tăng khi và chỉ khi với mọi n ∈ ℕ^*.

Đáp án chuẩn:

+) Nếu với mọi thì . Do đó dãy số là dãy số tăng.

+) Nếu là dãy số tăng thì do đó

BT 6: Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi P_n (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng.

a) Tính số tiền chị có trong ngân hàng sau 1 tháng

b) Tính số tiền chị có trong ngân hàng sau 3 tháng

c) Dự đoán công thức của P_n tính theo n

Đáp án chuẩn:

a) (triệu đồng).