CHƯƠNG 7_BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM, Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM

I. ĐẠO HÀM TẠI MỘT ĐIỂM

HĐ1: Tính vận tốc tức thời của viên bi tại thời điểm x_0=1(s) trong bài toán tìm vận tốc tức thời nêu ở trên.

Đáp án chuẩn:

v1=9,8

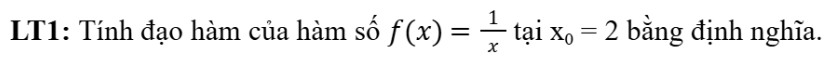
Đáp án chuẩn:

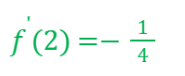
LT2: Tính đạo hàm của hàm số f (x) = x³  tại điểm x bất kì bằng định nghĩa.

Đáp án chuẩn:

f'x=3x²

II. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM

HĐ2: Cho hàm số y = f(x) có đồ thị (C) một điểm M₀ cố định thuộc (C) có hoành độ x₀ Với mỗi điểm M thuộc (C) khác M₀, kí hiệu x_M là hoành độ của điểm M và k_M là hệ số góc của cát tuyến M₀M. Giả sử tồn tại giới hạn hữu hạn k₀= xMx0k_M . Khi đó, ta coi đường thẳng M₀T đi qua M₀ và có hệ số góc k₀ là vị trí giới hạn của cát tuyến M₀M khi điểm M di chuyển dọc theo (C) dần tới M₀.s

Đường thẳng M₀T được gọi là tiếp tuyến của (C) tại điểm M₀, còn M₀ được gọi là tiếp điểm (Hình 3).

a) Xác định hệ số góc k₀ của tiếp tuyến M₀T theo x₀.

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀.

Đáp án chuẩn:

a) k0 =f'x0

b) y=f'x0x-x0+fx0

LT3: Viết phương trình tiếp tuyến của đồ thị hàm số y = 1/x tại điểm N (1;1)

Đáp án chuẩn:

y= -x+2

GIẢI BÀI TẬP CUỐI SGK

Bài 1. Tính đạo hàm của hàm số f(x) = 3x³ – 1 tại điểm x₀ = 1 bằng định nghĩa:

Đáp án chuẩn:

f'1=9.

Bài 2. Chứng minh rằng hàm số f(x) = |x| không có đạo hàm tại điểm x₀ = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0

Đáp án chuẩn:

Chứng minh :

+) hàm số fx=x không có đạo hàm tại điểm x0=0.

+) x>0 thì hàm số có đạo hàm f'x=1.

+) x<0 thì hàm số có đạo hàm f'x=-1

Vậy hàm số fx=x không có đạo hàm tại điểm x0=0 nhưng có đạo hàm tại mọi điểm x≠0.

Bài 3. Cho hàm y = –2x² + x có đồ thị (C).

a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2.

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6)

Đáp án chuẩn:

a) -7

b) y=-7x+8.

Bài 4. Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C(Q) = Q2 + 80Q + 3 500.

a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.

b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được

Đáp án chuẩn:

a) C'Q=2Q+80 (USD)

b) C'90=260 (USD) : Để sản xuất thêm 1 sản phẩm từ 90 lên 91 sản phẩm cần chi phí biên là 260 (USD)