BÀI TẬP CUỐI CHƯƠNG III

BT 1: Cho hàm số y = f(x) xác định trên khoảng (a;b) và x₀ ∈ (a;b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x₀ là:

A. = f(x₀)

B. = f(x₀)

C. =

D. == f(x₀)

Đáp án chuẩn: 

D.

BT 2: Tính các giới hạn sau:

a)
b)
c)
d)
e)
g)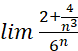                            

Đáp án chuẩn: 

a)
b)
c)
d)
e)
g)

BT 3: Tính các giới hạn sau:

a)

b)

c)

Đáp án chuẩn: 

a)
b)
c)

BT 4: Tính các giới hạn sau:

a)
b)
c)
d)
e)
g)

Đáp án chuẩn: 

a)
b)
c)
d)
e)
g)

BT 5: Cho hàm số f(x)=

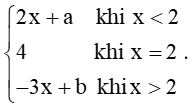
a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.

b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2?

c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?

Đáp án chuẩn: 

a) Hàm số không liên tục tại
b) Hàm số liên tục tại
c) và  

BT 6: Từ độ cao 55,8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 1/10 độ cao mà quả bóng đạt được trước đó. Gọi Sn là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất n lần. Tính lim Sn

Đáp án chuẩn: 

BT 7: Cho một tam giác đều ABC cạnh a. Tam giác A₁B₁C₁ có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A₂B₂C₂ có các đỉnh là trung điểm các cạnh của tam giác A₁B₁C₁, ..., tam giác A_{n +1}B_n+1C_n+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, ... Gọi p1,p2, ..., pn, ... và S1,S2, ..., Sn, ... theo thứ tự là chu vi và diện tích của các tam giác A₁B₁C₁, A₂B₂C₂, ..., AnBnCn, ...

a) Tìm giới hạn của các dãy số (pn) và (Sn). 

b) Tìm các tổng p1 + p2 + ... + pn + ... và S1 + S2 +... + Sn +... 

Đáp án chuẩn: 

a);

b) ;

BT 8: Một thấu kính hội tụ có tiêu cự là f. Gọi d và d′ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A′B′ của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính là =

a) Tìm biểu thức xác định hàm số d’ = φ(d).

b) Tìm Giải thích ý nghĩa của các kết quả tìm được.

Đáp án chuẩn: 

a) .
b) ; = ;