CHƯƠNG III: GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 1: GIỚI HẠN CỦA DÃY SỐ

I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

LT-VD 1Chứng minh rằng:

a) lim 0 = 0

b) = 0

Đáp án chuẩn:

a) Xét: với mọi => với mọi => lim 0 = 0

b) Xét: với mọi => lim

LT-VD 2: Chứng minh rằng lim = -4

Đáp án chuẩn:

Đặt

Lim =>Lim

LT-VD 3: Chứng minh rằng lim

Đáp án chuẩn:

0< =>

II. ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN

LT-VD 4: Tính các giới hạn sau:

a) Lim

b)

Đáp án chuẩn:

a) Lim

b)

III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN 

LT-VD 5: Tính tổng M =

Đáp án chuẩn:

LT-VD 6: Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng?

Đáp án chuẩn:

Thời gian đi hết quãng đường trên là :

=> Archilles đuổi kịp rùa sau giờ

IV. GIỚI HẠN VÔ CỰC

LT-VD 7: Tính lim ( - n³)

Đáp án chuẩn:

lim

LT-VD 8: Chứng tỏ rằng lim= 0

Đáp án chuẩn:

lim

BT 1: Cho hai dãy số (u_n), (v_n) với u_n = 3 + 1/n; v_n = 5 – 2/n². Tính các giới hạn sau:

a) lim u_n, lim v_n.

b) lim (u_n + v_n), lim (u_n − v_n), lim (u_n.v_n), lim u_n/v_n

Đáp án chuẩn:

a) ;

b) ; ; ; lim

BT 2: Tính các giới hạn sau:

a)

b)

c)
d)
e)
g)

Đáp án chuẩn:

a)

b)

c)
d)
e)
g)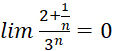

BT 3:

a) Tính tổng của cấp số nhân lùi vô hạn (u_n), với (u_n), với u₁ = 2/3,q = −1/4.

b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số. 

Đáp án chuẩn:

a)

b)

BT 4: Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn.

a) Tính diện tích Sn của hình vuông được tạo thành ở bước thứ n;

b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. 

Đáp án chuẩn:

a)
b)

BT 5: Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã). (Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)

Gọi u_n là khối lượng chất phóng xạ còn lại sau chu kì thứ n. 

a) Tìm số hạng tổng quát u_n của dãy số (u_n). 

b) Chứng minh rằng (u_n) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10⁻⁶ g. 

Đáp án chuẩn:

a)
b)
c) Cần ít nhất 30 chu kì tương ứng với 720 000 năm khối lượng chất phóng xạ đã cho ban đầu không còn độc hại với con người.

BT 6: Gọi C là nửa đường tròn đường kính AB = 2R, C₁  là đường gồm hai nửa đường tròn đường kính AB/2, C₂ là đường gồm bốn nửa đường tròn đường kính AB/4, Cn là đường gồm 2ⁿ nửa đường tròn đường kính AB/2ⁿ,... (Hình 4). Gọi p_n là độ dài của C_n, S_n là diện tích hình phẳng giới hạn bởi C_n và đoạn thẳng AB.

a) Tính p_n, S_n. 

b) Tìm giới hạn của các dãy số (p_n) và (S_n)

Đáp án chuẩn:

a) ;

b) ;