Trắc nghiệm Toán 10 kết nối bài 1 Mệnh đề
Bài trắc nghiệm có đáp án. Câu hỏi và bài tập trắc nghiệm Toán 10 bài 1 Mệnh đề - sách kết nối tri thức. Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.
Câu 1: Trong các câu sau, câu nào không phải là mệnh đề?
A. Buồn ngủ quá!
- B. Hình thoi có hai đường chéo vuông góc với nhau.
- C. 8 là số chính phương.
- D. Băng Cốc là thủ đô của Mianma.
Câu 2: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này!
d) 5+19=24.
e) 6+81=25.
f) Bạn có rỗi tối nay không?
g) x+2=11.
- A. 4
- B. 3
C. 2
- D. 1
Câu 3: Xét mệnh đề P:∃x ∈ R: 2x - 3 < 0 . Mệnh đề phủ định P_ của mệnh đề là:
A. “
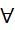 x ∈ R: 2x - 3
x ∈ R: 2x - 3 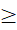 0”
0”- B. “
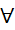 x ∈ R: 2x - 3
x ∈ R: 2x - 3 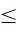 0”
0” - C. “
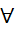 x ∈ R: 2x - 3
x ∈ R: 2x - 3  0”
0” - D. “
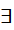 x ∈ R: 2x - 3
x ∈ R: 2x - 3 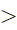 0”
0”
Câu 4: Mệnh đề phủ định của mệnh đề A: "∀x ∈ R: x ≥ 2 ⇒ x2 ≥ 4" là:
- A. "∀x ∈ R: x
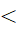 2 ⇒ x2 ≥ 4"
2 ⇒ x2 ≥ 4" - B. "∀x ∈ R: x ≥ 2 ⇒ x2
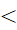 4"
4" C. "
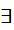 x ∈ R: x
x ∈ R: x 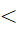 2 ⇒ x2
2 ⇒ x2 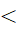 4"
4" - D. "
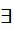 x ∈ R: x ≥ 2 ⇒ x2
x ∈ R: x ≥ 2 ⇒ x2 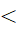 4"
4"
Câu 5: Trong các mệnh đề sau, mệnh đề nào sai?
A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi AC = BD .
- B. Điều kiện cần và đủ để số tự nhiên n chia hết cho 3 là tổng các chữ số của n chia hết cho 3.
- C. Nếu n là số nguyên lẻ thì n2 là số lẻ.
- D. Tam giác ABC là tam giác đều khi và chỉ khi AB = BC và
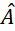 = 60°
= 60°
Câu 6: Mệnh đề nào đúng trong các mệnh đề sau?
- A.
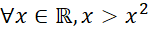
B.
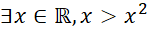
- C.
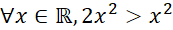
- D.
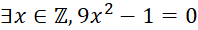
Câu 7: Mệnh đề nào sau đây đúng?
- A.
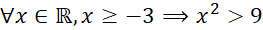
B.
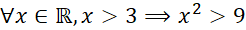
- C.
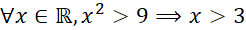
- D.
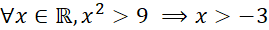
Câu 8: Cho biết P ⇒ Q là mệnh đề đúng. Trong các khẳng định sau, khẳng định nào đúng?
- A. P là điều kiện cần và đủ để có Q
- B. P là điều kiện cần để có Q
C. là điều kiện cần để có P
- D. Q là điều kiện cần và đủ để có P
Câu 9: Lập mệnh đề phủ định của mệnh đề: “ Số 6 chia hết cho 2 và 3”.
- A. Số 6 chia hết cho 2 hoặc 3.
- B. Số 6 không chia hết cho 2 và 3.
- C. Số 6 không chia hết cho 2 và chia hết cho 3.
D. Số 6 không chia hết cho 2 hoặc 3.
Câu 10: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. ∀x∈R, ∀y∈R, x+y2≥0
- B. ∀x∈R, ∃y∈R, x+y2≥0.
- C. ∃x∈R, ∀y∈R, x+y2≥0.
- D. ∃x∈R, ∀y∈R, x+y2≤0.
Câu 11: Mệnh đề phủ định của mệnh đề Px:"x2+3x+1>0 với mọi x" là
- A. Tồn tại x sao cho x2+3x+1>0
B. Tồn tại x sao cho x2+3x+1≤0.
- C. Tồn tại x sao cho x2+3x+1<0.
- D. Tồn tại x sao cho x2+3x+1=0
Câu 12: Cho mệnh đề chứa biến P(x): "x ∈ R: x + 8 ≤ x2". Mệnh đề đúng là:
A. P(5)
- B. P(3)
- C. P(0)
- D. P(-2)
Câu 13: Cho mệnh đề đúng: "Tất cả mọi người bạn của Nam đều biết bơi". Trong các mệnh đề sau, mệnh đề nào đúng?
- A. Chiến là bạn của Nam nên Chiến không viết bơi.
B. Minh không biết bơi nên Minh không là bạn của Nam.
- C. Thành không là bạn của Nam nên Thành không biết bơi.
- D. Bình biết bơi nên Bình là bạn của Nam.
Câu 14: Viết mệnh đề phủ định P¯ của mệnh đề P: ''Tất cả các học sinh khối 10 của trường em đều biết bơi''.
- A. P¯: ''Tất cả các học sinh khối 10 trường em đều biết bơi''.
B. P¯: ''Tất cả các học sinh khối 10 trường em có bạn không biết bơi''.
- C. P¯: ''Trong các học sinh khối 10 trường em có bạn biết bơi''.
- D. P¯: ''Tất cả các học sinh khối 10 trường em đều không biết bơi''.
Câu 15: Kí hiệu X là tập hợp các cầu thủ x trong đội tuyển bóng rổ, Px là mệnh đề chứa biến ''xcao trên 180cm''. Mệnh đề "∀x∈X, Px" khẳng định rằng:
- A. Có một số người cao trên 180cm là cầu thủ của đội tuyển bóng rổ.
- B. Bất cứ ai cao trên 180cm đều là cầu thủ của đội tuyển bóng rổ.
- C. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên 180cm.
D. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180cm.
Câu 16: Mệnh đề "∃x∈R, x2=2" khẳng định rằng:
- A. Chỉ có một số thực mà bình phương của nó bằng 2.
- B. Bình phương của mỗi số thực bằng 2.
C. Có ít nhất một số thực mà bình phương của nó bằng 2.
- D. Nếu x là một số thực thì x2=2.
Câu 17: Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. ∃n∈N, nn+11+6 chia hết cho 11.
- B. ∀x∈R, -x2<0.
- C. Không có số chẵn nào là số nguyên tố.
- D. Phương trình 3x2-6=0 có nghiệm hữu tỷ.
Câu 18: Trong các mệnh đề sau đây, mệnh đề nào đúng?
- A. ∀x∈R, x2≥x.
- B. ∀x∈R, x>1⇒x>1.
- C. ∀x∈R, x2>x.
D. ∃x∈R, x2
Câu 19: Cho x là số thực, mệnh đề nào sau đây đúng?
- A. ∀ x,x2>5⇒-5
B. ∀ x,x2>5⇒x>5 hoặc x<-5
- C. ∀ x,x2>5⇒x>±5.
- D. ∀ x,x2>5⇒x≥5 hoặc x≤-5.
Câu 20: Mệnh đề phủ định của mệnh đề Px:"∃x∈R:x2+2x+5 là số nguyên tố" là
A. ∀x∈R: x2+2x+5 là hợp số.
- B. ∀x∉R: x2+2x+5 là hợp số.
- C. ∃x∈R: x2+2x+5 là hợp số.
- D. ∃x∈R: x2+2x+5 là số thực.
Câu 21: Phủ định của mệnh đề Px:"∃x∈R,5x-3x2=1" là
A. "∀x∈R,5x-3x2≠1".
- B. "∃x∈R,5x-3x2=1".
- C. "∀x∈R,5x-3x2=1".
- D. "∃x∈R,5x-3x2≥1".
Câu 22: Cho mệnh đề Px:"∀x∈R,x2+x+1>0". Mệnh đề phủ định của mệnh đề Px là
- A. "∀x∈R,x2+x+1<0".
- B. "∀x∈R,x2+x+1≤0".
C. "∃x∈R,x2+x+1≤0".
- D. "∃x∈R,x2+x+1>0".
Câu 23: Trong các mệnh đề sau, mệnh đề nào là định lí?
- A. Nếu a+b chia hết cho 3 thì a,b đều chia hết cho 3.
- B. ∀x∈R,x>−2⇒x2>4
- C. ∀x∈R,x2>4⇒x>2
D. ∀x∈R,x>2⇒x2>4
Câu 24: Cho mệnh đề A: “∀x∈R,x2−x+7<0” Mệnh đề phủ định của A là:
- A. ∀x∈R,x2−x+7>0
B. ∃x∈R,x2− x+7≥0
- C. Không tồn tại x:x2−x+7<0
- D. ∀x∈R,x2−x+7>0
Câu 25: Trong các mệnh đề sau, mệnh đề nào đúng?
- A.
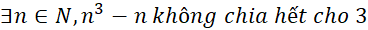
B.
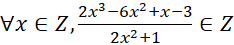
- C.

- D.
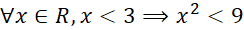
Xem toàn bộ: Giải bài 1 Mệnh đề

Bình luận