Câu 1: Một hộp gồm có 4 bi xanh và 5 bi đỏ. Lấy ngẫu nhiên hai viên bi trong hộp. Biến cố đối của biến cố D: “Hai viên bi cùng màu” là:

• A. $\bar{D}$ “Hai viên bi khác màu”;           

• B. $\bar{D}$ : “Hai viên bi có màu đỏ”;          
• C. $\bar{D}$: “Hai viên bi có màu xanh”;                
• D. $\bar{D}$: “Hai viên bi cùng màu”.

Câu 2: Đội tuyển của một lớp có 8 học sinh nam và 4 học sinh nữ. Trong buổi dự lễ trao thưởng, các học sinh được xếp thành 1 hàng ngang. Xác suất để xếp cho 2 học sinh nữ không đứng cạnh nhau là:

• A. $\frac{653}{660}$
• B. $\frac{7}{660}$
• C. $\frac{41}{55}$

• D. $\frac{14}{55}$

Câu 3: Chọn ngẫu nhiên 2 học sinh từ một tổ có 9 học sinh. Biết rằng xác suất chọn được 2 học sinh nữ bằng $\frac{5}{18}$, hỏi tổ có bao nhiêu học sinh nữ?

• A. 6;

• B. 5;

• C. 3;
• D. 4.

Câu 4:  Xác suất của biến cố A kí hiệu là P(A). Biến cố $\bar{A}$ là biến cố đối của A, có xác suất là P($\bar{A}$)

Chọn phát biểu sai trong các phát biểu sau:

• A. Với mọi biến cố A, 0 ≤ P(A) ≤ 1;
• B. P(Ω) = 1, P(∅) = 0;

• C. Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng xa 1;

• D. P($\bar{A}$ + P(A) = 1

Câu 5: Gieo hai đồng tiền một lần. Kí hiệu S, N lần lượt để chỉ đồng tiền lật sấp, lật ngửa. Mô tả không gian mẫu nào dưới đây là đúng?

• A. Ω = {S, N};
• B. Ω = {NN, SS};
• C. Ω = {SN, NS};

• D. Ω = {SN, NS, SS, NN}.

Câu 6: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Số kết quả thuận lợi cho biến cố B: “4 viên bi lấy ra có ít nhất một viên bi màu xanh” là:

• A. 10 626;
• B. 1 820;
• C. 7 566;

• D. 8 806.

Câu 7: Trên bàn có 3 quả táo và 4 quả cam. Xác định số phần tử không gian mẫu của phép thử lấy 2 quả ở trên bàn sau đó bỏ ra ngoài rồi lấy tiếp 1 quả nữa.

• A. 7 phần tử;
• B. 5 phần tử;

• C. 105 phần tử;

• D. 21 phần tử.

Câu 8: Kí hiệu nào sau đây là kí hiệu của biến cố chắc chắn?

• A. Ω;          

• B. ∅;           
• C. M;          
• D. c.

Câu 9: Hoạt động nào sau đây không phải là phép thử?

• A. Đặt 2 chiếc bút bi đỏ, 5 chiếc bút bi xanh và 3 chiếc bút bi tím lên bàn và đếm xem có bao nhiêu chiếc bút bi;    

• B. Chọn một trong ba bạn An, Bình, Cường tham gia cuộc thi chạy điền kinh;
• C. Chơi trò chơi gắp thú nhồi bông;             
• D. Chọn một quyển sách bất kì trên giá sách và đọc tên của quyển sách đó.

Câu 10: Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố A là:

• A. 3;

• B. 4;

• C. 5;
• D. 6.

Câu 11: Một nhóm có 3 bạn nam và 2 bạn nữ. Chọn ngẫu nhiên cùng lúc 2 bạn đi làm vệ sinh lớp. Số kết quả thuận lợi cho biến cố “Chọn được 1 bạn nam và 1 bạn nữ” là:

• A. 5;
• B. 4;
• C. 3;

• D. 6.

Câu 12: Một nhóm có 3 bạn nam và 2 bạn nữ. Chọn ngẫu nhiên cùng lúc 2 bạn đi làm vệ sinh lớp. Số phần tử của không gian mẫu của phép thử là:

• A. 10;

• B. 5;
• C. 15;
• D. 20.

Câu 13: Gọi A là biến cố của không gian mẫu . Phát biểu nào sau đây đúng?

• A. A ∈ Ω;

• B. A ⊂ Ω;

• C. Ω ∈ A;
• D. Cả 3 phương án trên đều đúng.

Câu 14: Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức $(2a+b)^4$ bằng

• A. 4;

• B. 5;
• C. 3;
• D. 6.

Câu 15: Hệ số của $x^3$ trong khai triển của $(3-2x)^5$ là:

• A. 4608;
• B. 720;

• C. –720

• D. –4608.

Câu 16: Trong khai triển $(x-2y)^4$ số hạng chứa $y^2$$y^2$ là:

• A. 24;

• B. –24;
• C. 35;
• D. –35.

Câu 17: Trong khai triển $(x^{2} - 2x)^5$ hệ số của số hạng chứa $x^6$ là:

• A. – 80;
• B. – 50;
• C. 50;

• D. 80.

Câu 18: Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức $(m+2n)^5$bằng

• A. 4;

• B. 5;

• C. 6;
• D. 7.

Câu 19: Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.

• A. n = 6;
• B. n = 12;

• C. n = 8;

• D. n = 15.

Câu 20: Cho tập hợp M = {a; b; c}. Số hoán vị của ba phần tử của M là:

• A. 4;           
• B. 5;            

• C. 6;            

• D. 7.

Câu 21: Có bao nhiêu cách xếp 8 người vào một bàn tròn

• A. 720;

• B. 5040;

• C. 40320;
• D. 35280.

Câu 22: Có bao nhiêu vectơ khác vectơ được tạo thành từ 10 điểm phân biệt khác nhau

• A. 45;

• B. 90;

• C. 35;
• D. 55.

Câu 23: Nếu thì x thoả mãn điều kiện nào sau đây

• A. x > 11;

• B. 2x + 3 > 20;

• C. x – 2 ≤ 7;
• D. 2x – 4 < 15.

Câu 24: Một tổ gồm 12 học sinh trong đó có bạn An. Hỏi có bao nhiêu cách chọn 4 em đi trực trong đó phải có An:

• A. 990;
• B. 495;
• C. 220;

• D. 165.

Câu 25: Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách sắp xếp để nam, nữ ngồi xen kẽ

• A. 6;

• B. 12;

• C. 36;
• D. 26.

Câu 26: Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.

 Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.

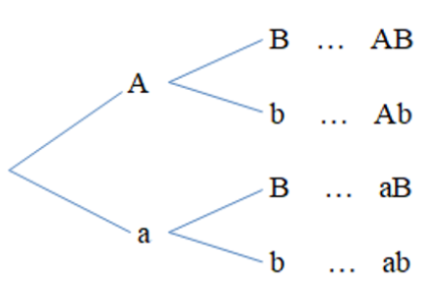
Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:

• A. 4;           

• B. 2;            
• C. 8;            
• D. 16.

Câu 27: Trên giá sách có 7 quyển sách Tiếng Nga khác nhau, 9 quyển sách Tiếng Anh khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn hai quyển sách khác loại là

• A. 24;
• B. 504;

• C. 191;

• D. 305.

Câu 28: Giả sử một công việc có thể được thực hiện theo một trong hai phương án. Phương án thứ nhất có 10 cách thực hiện, phương án thứ hai có 5 cách thực hiện không trùng với bất kì cách nào của phương án thứ nhất. Khi đó, công việc có thể được thực hiện theo bao nhiêu cách?

• A. 50 cách;           

• B. 15 cách;                     

• C. 1 cách;              
• D. 125 cách.

Câu 29: Số nghiệm của phương trình $\sqrt{8-x^2}$ = $\sqrt{x+2}$

• A. 0;

• B. 1;

• C. 2;
• D. 3.

Câu 30: Số nghiệm của phương trình $\sqrt{2x - 4}$ = $\sqrt{x^2-3x}$ là:

• A. 0;           
• B. 2;            
• C. 3;            

• D. 1.

Câu 31: Số nghiệm của phương trình $\sqrt{2x^2-2x+4}$ = $\sqrt{x^2-x+2}$

• A.0;

• B.1;
• C.2;
• D.3.

Câu 32: Giá trị của m để (m – 1)$x^2$– 2(m + 1)x + m + 3 ≤ 0 là bất phương trình bậc hai một ẩn là:

• A. m ≠ –3;            
• B. m ≠ –1;            
• C. m = 1;              

• D. m ≠ 1.

Câu 33: Tập nghiệm của bất phương trình $x^2$–x–6≤0 là:

• A. (–∞; – 3]∪[2; + ∞);
• B. [– 3; 2];

• C. [– 2; 3];

• D. (– ∞; – 2]∪[3; + ∞) ;

Câu 34:Các giá trị m để bất phương trình $x^2$ – (m + 2)x + 8m + 1 < 0 luôn có nghiệm

• A. m < 28;

• B. m < 0 hoặc m > 28

• C. 0 < m < 28
• D. m > 0.

Câu 35:  Cho tam thức bậc hai 

f(x)=$x^2$–10x+2. Kết luận nào sau đây đúng?

• A. f(–2) < 0;         
• B. f(1) > 0;            

• C. f(–2) > 0;          

• D. f(1) = 0.

Câu 36: Biểu thức nào sau đây là tam thức bậc hai?

• A. f(x)= 2$x^3$ + 3$x^2$ + 1          
• B. f(x)=–$x^2$ + 2x -10          

• C. f(x) = x – 4;                

• D. f(x) = –7.

Câu 37: Tam thức nào sau đây nhận giá trị âm với mọi x < 1

• A. f(x)= $x^{2}$ - 5x + 6
• B. f(x)=$x^2$-16
• C. f(x)=$x^2$ + 2x + 3

• D. f(x)=–$x^2$ + 5x -4

Câu 38: Biểu thức nào sau đây là tam thức bậc hai

• A. f(x) = x + 2;
• B. f(x)=$2x^3$+2$x^2$–1;

• C. f(x)= $x^{2}$–3x;

• D. f(x) = 2x – 1.

Câu 39: Tam thức y= – $x^{2}$–3x–4 nhận giá trị âm khi và chỉ khi

• A. x < 4 hoặc x > – 1;
• B. x < 1 hoặc x > 4;
• C. – 4 < x < 4;

• D. x ∈ ℝ.

Câu 40: Biểu thức f(x)=($m^2$+2)$x^2$–2(m–2)x+2 luôn nhận giá trị dương khi và chỉ khi

• A. m ≤ - 4 hoặc m ≥ 0;

• B. m < - 4 hoặc m > 0;

• C. – 4 < m < 0;
• D. m < 0 hoặc m > 4.