BÀI TẬP CUỐI CHƯƠNG 4

Bài 1. Cho tam giác ABC biết a = 49; b = 26,4; = 4720′. Tính hai góc và cạnh c.

Giải rút gọn: 

c = ≈ 37

= => sinA = = ≈ 0,982 ≈ 797’

=> = 180 - (4720’ + 797’) = 5333’

Bài 2. Cho tam giác ABC. Biết a = 24, b = 13, c = 15. Tính các góc

Giải rút gọn: 

cosA = = ≈ 11749’

= => sinB = ≈ 0,48 ≈ 2841’=>  ≈  3330’

Bài 3. Cho tam giác ABC có a = 8, b = 10, c = 13.

a. Tam giác ABC có góc tù không?

b. Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.

c. Lấy điểm D đối xứng với A qua C. Tính độ dài BD.

Giải rút gọn: 

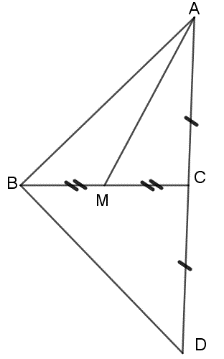
a) cos C = = < 0 => góc C tù.

b) MC = MB = 4.

ΔMAC : AM² = 4² + 10² - 2.4.10. = => AM =

p = ( 8 + 10 + 13 ) : 2 =

S = ≈ 39,98 => R = ≈ 6,5

c) cos = cos = =       ; AD = 2.AC = 20

ΔBDA : BD² = 20² + 13² – 2.20.13. => BD = ≈ 12,6

Bài 4. Cho tam giác ABC có , b = 8, c = 5. Tính:

a. Các cạnh a và các góc

b. Diện tích tam giác ABC;

c. Bán kính đường tròn ngoại tiếp và đường cao AH.

Giải rút gọn: 

a) a² = 8² + 5² – 2.8.5.cos 120⁰ = 129 => a =

= sin B = ≈ 3735’ => ≈ 2225’.

b) S = .8.5.sin 120⁰ = 10

c) R = =  ; h_a = =

Bài 5. Cho hình bình hành ABCD.

a. Chứng minh 2(AB² + BC²) = AC² + BD²

b. Cho AB = 4, BC = 5, BD = 7. Tính AC.

Giải rút gọn: 

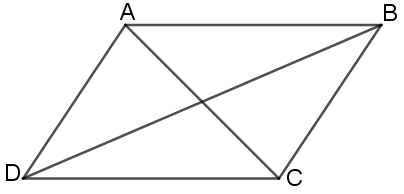
a) AC² = BC² + BA² – 2.BC.BA.cos B

    BD² = BC² + DC² – 2.BC. DC. cos C= BC² + AB² + 2.BC. AB. cos B

=> AC² + BD² = 2(AB² + BC²).

b) AC² = 2.(4² + 5²) - 7² = 33 => AC ≈ 5,7.

Bài 6. Cho tam giác ABC có a = 15, b = 20, c = 25.

a. Tính diện tích tam giác ABC.

b. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Giải rút gọn: 

a) p = ( 15 + 20 + 25) : 2 = 30 => S = = 150.

b) R = = 12,5.

Bài 7. Cho tam giác ABC. Chứng minh rằng: cot A + cot B + cot C =

Giải rút gọn: 

cos A = ; sin A = cot A = =

Tương tự : cot B = ; cot C =

=> cot A + cot B + cot C =

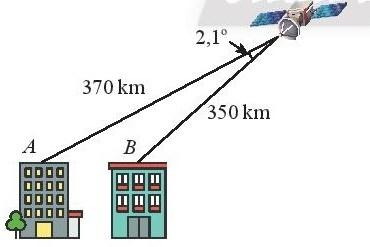
Bài 8. Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370km, 350km và góc nhìn từ vệ tinh đến A và B là 2,1.

Giải rút gọn: 

Gọi vị trí của vệ tinh là C

AB² = 350² + 370² - 2. 350. 370. cos(2,1) ≈ 574 => AB ≈ 24 (km).

Bài 9. Hai chiếc tàu thủy P và Q cách nhau 300m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp AB dưới các góc . Tính chiều cao của tháp hải đăng đó.

Giải rút gọn: 

= 180⁰ - 48⁰ = 132, = 180⁰ – 132⁰ – 35⁰ = 13⁰

ΔAPQ: = AQ = ≈ 765 (m) =>AB ≈ 765. sin48 ≈ 569 (m)

Bài 10. Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là h = 1,2m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được . Tính chiều cao CD của tháp.

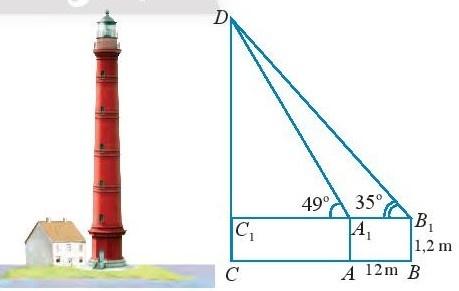
Giải rút gọn: 

= 180 - 49 = 131, = 180 + 35 ) = .

= => DA₁ ≈ 28,45 (m)

sin = => DC₁ ≈ 21,47 (m) => CD = 21,47 + 1,2 = 22,67 (m)