BÀI TẬP CUỐI CHƯƠNG II

Bài 1. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy:

a. -2x + y - 1 ≤ 0;                                    b. -x + 2y > 0

c. x - 5y < 2;                                              d. -3x + y + 2 ≤ 0;

e. 3(x - 1) + 4(y - 2) < 5x - 3

Giải rút gọn: 

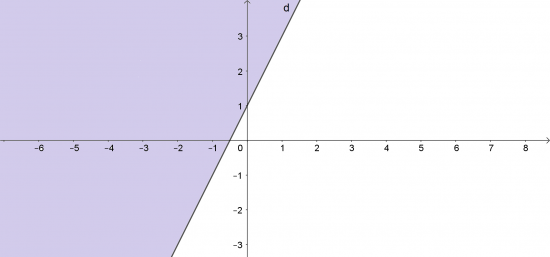
a. Qua 2 điểm (; 0) và (0; 1) vẽ đường thẳng d: -2x + y - 1 = 0 

   Điểm O(0; 0) ∉ d và -2. 0 + 0 - 1 = -1 < 0 

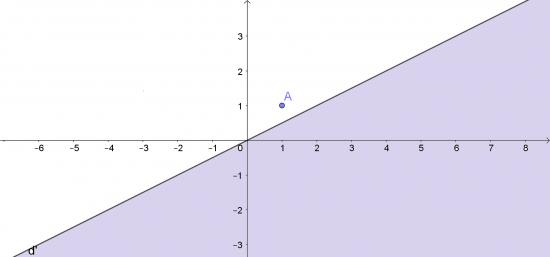
b. Qua 2 điểm (0;0) và (2;1) vẽ đường thẳng d': -x + 2y = 0 

Điểm A(1; 1) ∉ d' và -1 + 2.1 = 1 > 0 

=> miền nghiệm là nửa mặt phẳng không kể bờ d' và chứa điểm A.

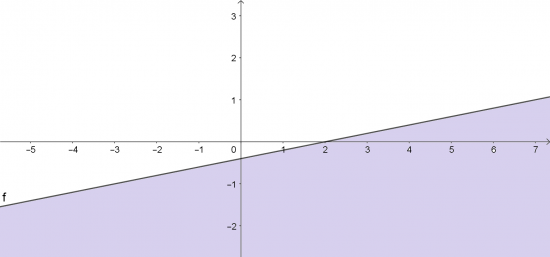
c. Qua 2 điểm (2; 0) và (0; ) vẽ đường thẳng f: x - 5y - 2 = 0 

Điểm O(0;0) ∉ f và 0 - 5. 0 - 2 = -2 < 0 

=> Miền nghiệm là nửa mặt phẳng không kể bờ f và chứa gốc tọa độ O.

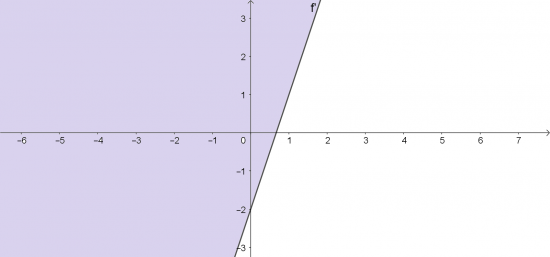
d. Qua 2 điểm (; 0) và (0; -2) vẽ đường thẳng f ': -3x + y + 2 = 0 

Điểm O(0; 0) ∉ f ' và -3. 0 + 0 + 2 = 2 > 0. 

=> Miền nghiệm là nửa mặt phẳng kể cả bờ f' và không chứa gốc tọa độ O.

e. 3x - 3 + 4y - 8 < 5x - 3 <=> x - 2y + 4 > 0

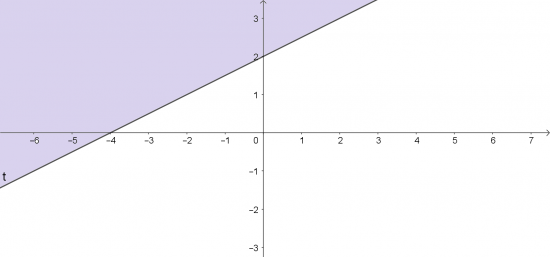
Qua 2 điểm (-4; 0) và (0; 2) vẽ đường thẳng t: x - 2y + 4 = 0 

Điểm O(0; 0) ∉ t và 0 - 2. 0 + 4 > 0. 

=> Miền nghiệm là nửa mặt phẳng không kể bờ t và chứa gốc tọa độ O.

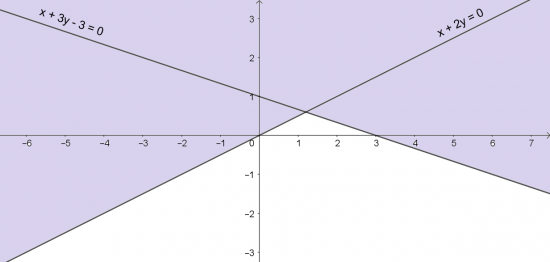
Bài 2. Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy:

Giải rút gọn: 

Bài tập 3. Một công ty dự định sản xuất hai loại sản phẩm A và B. Các sản phẩm này được chế tạo từ ba loại nguyên liệu I, II và III. Số kilogam dự trữ từng loại nguyên liệu và số kilogam từng loại nguyên liệu cần dùng để sản xuất ra 1 kg sản phẩm được cho trong bảng sau:

Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất? Biết rằng, mỗi kilogam sản phẩm loại A lãi 30 triệu đồng, mỗi kilogam sản phẩm loại B lãi 50 triệu đồng.

Giải rút gọn: 

Gọi số kilogam sản phẩm loại A ,loại B sản xuất được là x, y (kg)

Ta có :        

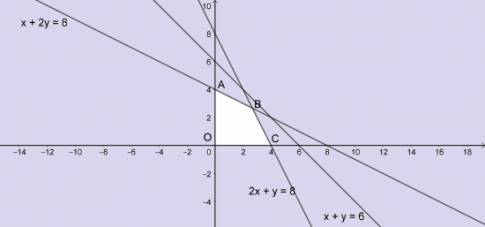
+) A là giao điểm của đường thẳng x + 2y = 8 và Oy => A(0; 4)

+) B là giao điểm của hai đường thẳng 2x + y = 8 và x + 2y = 8 => B()

+) C là giao điểm của đường thẳng 2x + y = 8 và Ox => C (4; 0)

+) Số tiền lãi thu được là : F = 30x + 50y ( triệu đồng)

+) F(O) = 0; F(A) = 200; F(B)  ≈ 213,3 ; F(C) = 120

+) Giá trị lớn nhất F = 213,3 tại  

=> sản xuất sản phẩm và sản phẩm

Bài 4. Một công ty cần mua các tủ đựng hồ sơ. Có hai loại tủ: Tủ loại A chiếm 3m² sàn, loại này có sức chứa 12m³ và có giá 7,5 triệu đồng; tủ loại B chiếm 6m² sàn, loại này có sức chứa 18m³ và có giá 5 triệu. Cho biết công ty chỉ thu xếp được nhiều nhất là 60m² mặt bằng cho chỗ đựng hồ sơ và ngân sách mua tủ không quá 60 triệu đồng. Hãy lập kế hoạch mua sắm để công ty có được thể tích đựng hồ sơ lớn nhất.

Giải rút gọn: 

Gọi số tủ loại A, loại B cần mua là x, y ( tủ)

Ta có :          

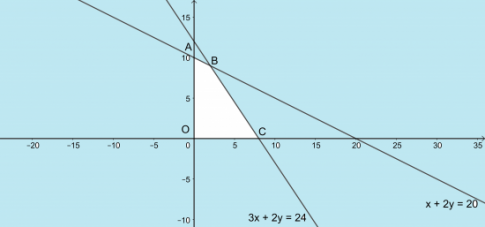
+) A là giao điểm của đường thẳng x + 2y =20  với Oy => A(0; 10)

+) C là giao điểm của đường thẳng 3x + 2y = 24 với Ox => C(8; 0)

+) B là giao điểm của hai đường thẳng x + 2y = 20 và 3x + 2y = 24 => B(2;9)

+) Thể tích đựng hồ sơ là: F = 12x + 18y (m³)

+) F(O) = 0; F(A) = 180; F(B) = 186; F(C) = 96

 => Giá trị lớn nhất F = 186 tại B(2; 9) => mua 2 tủ đựng loại A và 9 tủ đựng loại B.

Bài 5. Một nông trại thu hoạch được 180kg cà chua và 10 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10kg cà chua cùng với 1 kg hành tây và khi bán lãi thu được 200 nghìn đồng, còn để làm được một hũ tương cà loại B  cần 5kg cà chua cùng với 0,25kg hành tây và khi bán lãi thu được 150 nghìn đồng. Thăm dò thị hiếu của khách hàng cho thấy cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B, Hãy giúp chủ nông trại lập kế hoạch làm tương cà để có được nhiều tiền lãi nhất.

Giải rút gọn: 

Gọi số hũ tương cà loại A, loại B là x, y ( hũ)

Ta có:         

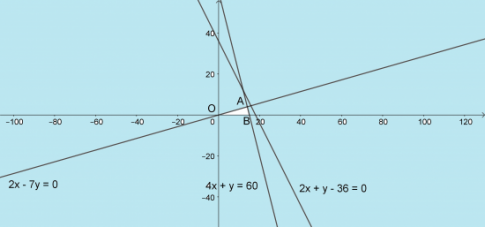
Miền nghiệm là miền tam giác OAB với 3 đỉnh O(0; 0); A(14; 4) và B(15; 0).

Số tiền lãi thu được là : F = 200x + 150y (nghìn đồng)

F(O) = 0; F(A) = 3400 ; F(B) = 3000

Giá trị lớn nhất F = 3 400 000 đồng tại A(14; 4)

=> làm 14 hũ tương cà loại A và 4 hũ tương cà loại B

Bài 6. Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày, máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng.

Giải rút gọn: 

Gọi sản lượng sản phẩm X , sản phẩm Y sản xuất trong 1 ngày là x, y (tấn)

Ta có :           ⬄

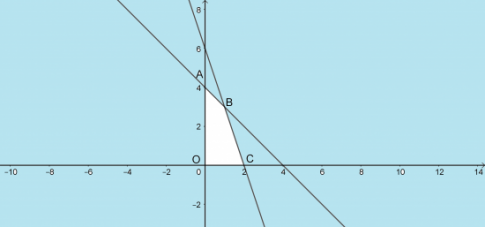
Miền nghiệm là miền tứ giác OABC với các đỉnh O(0; 0); A(0; 4); B(1; 3) ; C(2; 0).

Số tiền lãi thu được là : F = 10x + 8y ( triệu đồng)

F(O) = 0; F(A) = 32; F(B) = 34; F(C) = 20 ; 

Giá trị lớn nhất F = 34 tại B(1; 3).

=> sản xuất 1 sản phẩm loại X và 3 sản phẩm loại Y .