BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

KHỞI ĐỘNG

Hai đường thẳng d: = -x - 2 và d': y = x + 1 chia mặt phẳng tọa độ thành bốn miền khác nhau (không tính đường thẳng d và d') như hình bên.

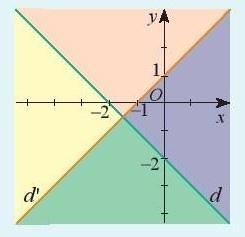
Để kí hiệu một trong bốn miền đó, người ta đã tạo nhãn:

Hãy đặt nhãn này vào miền phù hợp.

Giải rút gọn: 

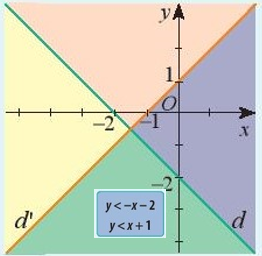
1. KHÁI NIỆM VỀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bài 1: Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng. 

a. Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.

b. Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên? 

(20; 40), (40; 20); (-30; 10).

Giải rút gọn: 

a.

b. (20; 40) thỏa mãn các bất phương trình.

Bài 2: Hãy chỉ ra hai nghiệm của bất phương trình trong Ví dụ 1.

Giải rút gọn: 

a. (0; 0) ; (0; 1)                                    b. (0; 0) ; (1; -1) 

c. (0; 1) ; ( 1; 1)                                   d. (0; 0) ; (1; 1)

2. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bài 1: Cho hệ bất phương trình:

Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?

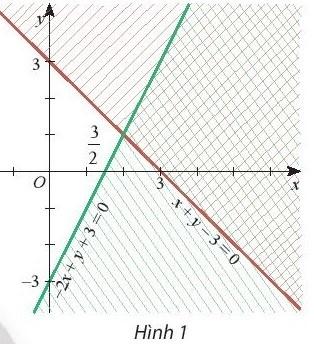
Giải rút gọn: 

Miền nghiệm của hệ bất phương trình là miền không gạch chéo .

Bài 2: Biểu diễn miền nghiệm của hệ bất phương trình:

Giải rút gọn: 

3. TÌM GIÁ TRỊ LỚN NHẤT HOẶC GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC F = ax + by TRÊN MỘT MIỀN ĐA GIÁC

Bài 1: Một người bán nước giải khát đang có 24g bột cam, 9l nước và 210g đường để pha chế hai loại nước cam A và B. Để pha chế 1l nước cam loại A cần 30g đường, 1l nước và 1g bột cam; để pha chế 1l nước cam loại B cần 10g đường, 1l nước và 4g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất?

Giải rút gọn: 

Gọi số lít nước cam loại A , loại B pha chế được là x, y .

Ta có:

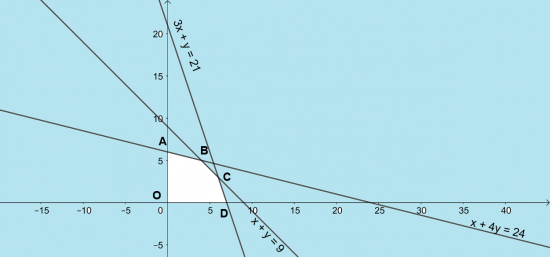
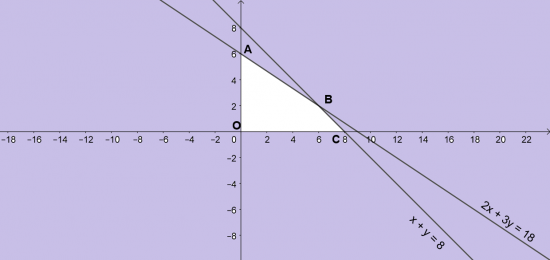
+) Điểm A là giao điểm của đường thẳng x + 4y = 24 với Oy => A(0; 6)

+) Điểm D là giao điểm của đường thẳng 3x + y = 21 với Ox => D (7; 0)

+) Điểm C là giao điểm của đường thẳng 3x + y = 21  và x + y = 9 => C ( 6; 3)

+) Điểm B là giao điểm của đường thẳng x + 4y = 24 và x + y = 9 => B ( 4;5)

+) Số tiền lãi thu được: F = 60x + 80y ( nghìn đồng)

+) F(O) = 0 ; F(A) = 480; F(B) = 640; F(C) = 600; F(D) = 420

=> Giá trị lớn nhất  của F(x) = 640 nghìn đồng tại B(4; 5).

Vậy để có lãi cao nhất cần sản xuất 4 lít nước cam loại A và 5 lít nước cam loại B 

BÀI TẬP CUỐI SGK

Bài 1. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:

Giải rút gọn: 

a. 

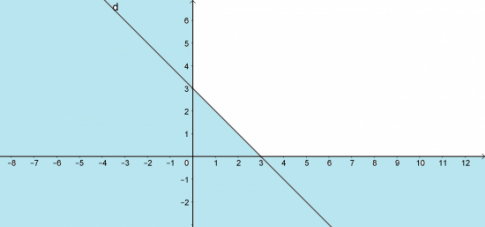
b. 

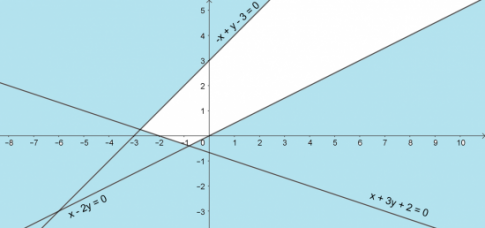
c.  

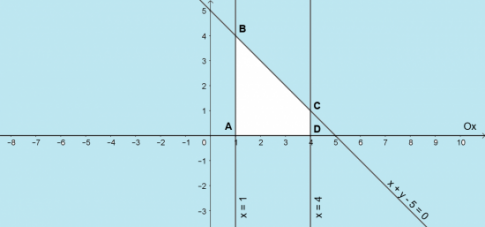
Bài 2. Một nhà máy sản xuất hai loại thuốc trừ sâu nông nghiệp là A và B. Cứ sản xuất mỗi thùng loại A thì nhà máy thải ra 0,25kg khí carbon dioxide (CO2) và 0,60kg khí sulfur dioxide (SO2), sản xuất mỗi thùng loại B thì thải ra 0,50kg CO2 và 0,20kg SO2. Biết rằng, quy định hạn chế sản lượng CO2 của nhà máy tối đa là 75kg và SO2 tối đa là 90kg mỗi ngày.

a. Tìm hệ bất phương trình mô tả số thùng mỗi loại thuốc trừ sâu mà nhà máy có thể sản xuất mỗi ngày để đáp ứng các điều kiện hạn chế trên. Biểu diễn miền nghiệm của hệ bất phương trình đó trên mặt phẳng tọa độ.

b. Việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày có phù hợp với quy định không?

c. Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày có phù hợp với quy định không?

Giải rút gọn: 

a. Gọi số thùng thuốc trừ sâu loại A, loại B là x, y

   Ta có : 

b. 0,25. 100 + 0,5. 80 = 65 < 75 (thỏa mãn)

    0,6. 100 + 0,2. 80 = 76 < 90 (thỏa mãn)

=> phù hợp với quy định.

c. 0,25. 60 + 0,5. 160 = 95 > 75 (không thỏa mãn)

   0,6. 60 + 0,2. 160 = 68 < 90 (thỏa mãn)

=> không phù hợp với quy định.

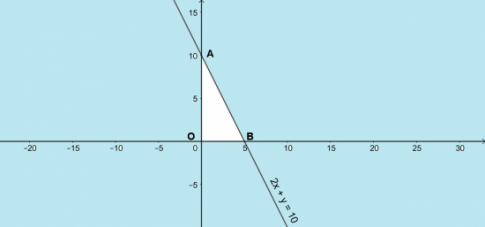
Bài 3. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó. 

Giải rút gọn: 

Ta có:

Bài 4. Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm.  Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.

Giải rút gọn: 

Gọi số tấm thiệp loại nhỏ, loại lớn là x, y.

Ta có:

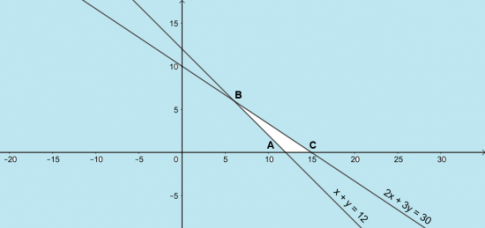
+) Điếm A là giao điểm của đường thẳng x + y = 12 và Ox => A (12;0)

+) Điểm C là giao điểm của đường thẳng 2x + 3y = 30 và Ox => C (15;0)

+) Điểm B là giao điểm của đường thẳng x + y =12 và 2x + 3y = 30 => B(6; 6)

+) Gọi số tiền bán thiệp là : F = 10x + 20y ( nghìn đồng)

+) F(A) = 120; F(C) = 150; F(B) = 180

 => Giá trị lớn nhất F(x;y) = 180 tại B(6, 6) => vẽ 6 tấm thiệp mỗi loại

Bài 5. Trong một tuần, bạn Mạnh có thể thu xếp được tối đa 12 giờ để tập thể dục giảm cân bằng hai môn: đạp xe và tập cử tạ tại phòng tập. Cho biết mỗi giờ đạp xe sẽ tiêu hao 350 calo và không tốn chi phí, mỗi giờ tập cử tạ sẽ tiêu hao 700 calo với chi phí 50000 đồng/ giờ. Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Hãy giúp bạn Mạnh tính số giờ đạp xe và số giờ tập tạ một tuần trong hai trường hợp sau:

a. Mạnh muốn chi phí luyện tập là ít nhất.

b. Mạnh muốn số calo tiêu hao là nhiều nhất.

Giải rút gọn: 

Gọi số giờ đạp xe, tập cử tạ trong một tuần là x; y.

Ta có : ⬄

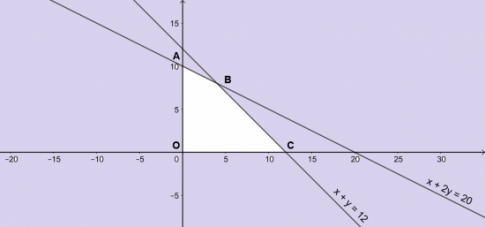
+) A là giao điểm của đường thẳng x + 2y = 20 và Oy => A( 0;10)

+) C là giao điểm của đường thẳng x + y = 12 và Ox => C(12; 0)

+) B là giao điểm của hai đường thẳng x + y = 12 và x + 2y = 20 => B(4; 8)

a. Chi phí luyện tập là: F = 50y (nghìn đồng)

   F(O) = 0; F(A) = 500 ; F(C) = 0 ; F(B) = 400

  Giá trị nhỏ nhất F = 0 tại O(0; 0) và C (12, 0).

  Vậy Mạnh không tập hoặc đạp xe 12 giờ/ tuần và không tập tạ.

b. Số calo tiêu hao là  K = 350x + 700y 

   K(O) = 0; K(A) = 7000; K(B) = 7000 ; K(C) = 4200

   Giá trị lớn nhất của K = 7000 calo tại A(0; 10) và B(4; 8).

    Vậy Mạnh tập 10 giờ cử tạ hoặc 4 giờ đạp xe và 8 giờ cử tạ.