BÀI 3. CÁC PHÉP TOÁN TRÊN TẬP HỢP

1. HỢP VÀ GIAO CỦA CÁC TẬP HỢP

Bài 1: Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu "+" là đạt, dấu "-" là không đạt):

a. Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.

b. Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn mà ngoại ngữ.

c. Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Giải rút gọn: 

a)

  .
b) .
c)

Bài 2: Xác định các tập hợp A ∪ B và A ∩ B, biết:

a. A = {a; b; c; d; e}, B = {a; e; i; u}

b. A = {x ∈R | + 2x - 3 = 0}, B = {x ∈R | |x| = 1}

Giải rút gọn: 

a. A ∪ B = {a; b; c; d; e; i; u} ;  A ∩ B = {a; e}

b. A ∪ B = {-3; -1; 1};     A ∩ B = {1}

Bài 3: Cho A = {(x; y) | x, y  ∈ R, 3x - y = 9}, B = {(x; y) | x, y ∈ R, x - y = 1}. Hãy xác định A ∩ B.

Giải rút gọn: 

(x; y)  thoả mãn  

=> x = 4 ; y = 3 => .

Bài 4: Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khám giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh này. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?

Giải rút gọn: 

Số khán giả tham gia bình chọn là: 85 + 72 - 60 = 97 (khán giả)

Số khán giả không tham gia bình chọn là: 100 - 97 = 3 (khán giả)

2. HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP CON

Bài 1: Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Khám phá 1.

a. Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.

b. Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.

Giải rút gọn: 

a)                                              b) .

Bài 2: Cho các tập hợp E = {x ∈N| x < 8}, A = {0; 1; 2; 3; 4}, B = {3; 4; 5}.

Xác định các tập hợp sau đây:

a. A\B, B\A và (A\B) ∩ (B\A);

b. (A∩B) và (A) ∪ (B)

c. (A∪B) và (A) ∩ (B)

Giải rút gọn: 

a) .
b) ;

c) (A∪B) = {6; 7} ; (A) ∩ (B)  = {6; 7}1

Bài 3: Xác định các tập hợp sau đây:

a. (1; 3) ∪ [-2; 2]                                            b. (-∞; 1) ∩ [0; π]

c. [; 3)\ (1; +∞)                                             d. [-1; +∞)

Giải rút gọn: 

a)                                                      b)

                                                       d)

BÀI TẬP CUỐI SGK

Bài 1: Xác định các tập hợp A ∪ B và A ∩ B với 

a. A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím};

b. A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.

Giải rút gọn: 

a) đỏ; cam; vàng; lục; lam; chàm; tím ; lục; lam

b)

Bài 2: Xác định tập hợp A giao B trong mỗi trường hợp sau: 

a. A = {x ∈R | - 2 = 0}, B = {x ∈ R | 2x - 1 < 0};

b. A = {(x, y) | x, y ∈ R, y = 2x - 1}; B = {(x; y) | x, y ∈ R , y = -x + 5};

c. A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.

Giải rút gọn: 

a) .

b) .

c) là tập hợp các hình vuông. 

Bài 3: Cho E = { x ∈ N | x < 10}, A = { x ∈ E | x là bội của 3}, B = { x ∈ E | x là ước của 6}. Xác định các tập hợp A\B, B\A, C_EA, C_EB, C_E(A∪B), C_E(A∩B)

Giải rút gọn: 

E = {0;1;2;3;4;5;6;7;8;9} ;         A = {0;3;6;9} ;                B = {1;2;3;6}

A\B = {0; 9} ;                            B\A = {1; 2}

C_EA = {1; 2; 4; 5; 7;8 } ;           C_EB = {0; 4; 5; 7; 8; 9}

C_E(A∪B) = {4; 5; 7; 8} ;           C_E(A∩B) = {0; 1; 2; 4; 5;7; 8; 9}

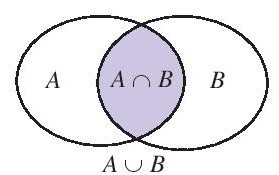
Bài 4. Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập hợp con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.

a. A và A ∪ B                                      b. A và A ∩ B

Giải rút gọn: 

a) A ⊂ (A ∪ B)                                    b) (A ∩ B) ⊂ A

Bài 5. Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:

a. Có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?

b. Có bao nhiêu học sinh không thích cả hai môn này?

Giải rút gọn: 

a. Số học sinh thích ít nhất một trong hai môn là: 20 + 16 - 12 = 24 (học sinh)

b. Số học sinh không thích cả hai môn này là: 35 - 24 = 11 (học sinh)

Bài 6. Xác định các tập hợp sau đây:

a. (-∞; 0] ∪ [-π; π];                                        b. [-3,5 ; 2] ∩ (-2 ; 3,5);

c. (-∞; ] ∩ [1; +∞);                                    d. (-∞; ] \ [1; + ∞).

Giải rút gọn: 

a. (-∞; π]                                                        b. (-2; 2]

c. [1; ]                                                       d. (-∞; 1)