CHƯƠNG I. MỆNH ĐỀ VÀ TẬP HỢP

BÀI 3. CÁC PHÉP TOÁN TRÊN TẬP HỢP

1. HỢP VÀ GIAO CỦA CÁC TẬP HỢP

HĐKP 1:

a) A={a$_{1}$;a$_{2}$;a$_{5}$;a$_{6}$;a$_{7}$;a$_{8}$;a$_{10}$},

B={a$_{1}$;a$_{3}$;a$_{5}$;a$_{6}$;a$_{8}$;a$_{10}$}.
b) C={a$_{1}$;a$_{5}$;a$_{6}$;a$_{8}$;a$_{10}$}.
c) D={a$_{1}$;a$_{2}$;a$_{3}$;a$_{5}$;a$_{6}$;a$_{7}$;a$_{8}$;a$_{10}$}.

Kết luận:

Cho hai tập hợp A và B 

Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A U B.

AUB={x|x$\in $Ahoặc x$\in $B}.

Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A$\cap $B.

A$\cap $B={x|x$\in $Avà x$\in $B}.

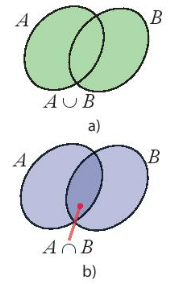
Ví dụ 1 (SGK – tr22)

Ví dụ 2 (SGK – tr22)

Nhận xét:

- Nếu A và B là hai tập hợp hữu hạn thì n(A∪B)=n(A)+n(B)-n(A∩B)

- Nếu A và B không có phần tử chung, tức A$\cap $B=∅, thì 

n(AUB)=n(A)+n(B).

Thực hành 1:

a) A U B=a;b;c;d;e;i;u,

A$\cap $B={a;e}.
b) A={-3;1},B={-1;1}. 

Từ đó, A U B={-3;-1;1},A $\cap $ B={1}.

Thực hành 2:

 Ta thấy (x;y) $\in $ A $\cap $ B,

x và y phải thoả mãn {3x-y=9 x-y=1.

(Nói cách khác, A $\in $ B là tập nghiệm của hệ phương trình này). Giải hệ phương trình, nhận được nghiệm (4;3). 

Vậy A $\in $ B={(4;3)}.

Vận dụng:

Kí hiệu E là tập hợp các khán giả bình chọn cho thí sinh A,F là tập hợp các khán giả bình chọn cho thí sinh⁡B.

Theo giả thiết, ta có n(E)=85,n(F)=72 và n(E $\in $ F)=60.

Tập hợp các khán giả đã bình chọn chính là EF. Ta có

n(EF)=n(E)+n(F)-n(E $\in $ F)=85+72-60=97.

Vậy có 97 khán giả đã tham gia bình chọn và 3 khán giả không tham gia bình chọn.

2. HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP CON 

HĐKP 2: 

a) E={a$_{2}$;a$_{7}$},

b) F={a$_{3}$;a$_{4}$;a$_{9}$}.

Kết luận:

Cho hai tập hợp A và B.

Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\B.

A\B={x|x∈A và x∉B}.

Nếu A là tập con của E thì hiệu E\A gọi là phần bù của A trong E, kí hiệu C$_{E}$A.

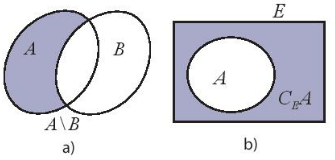
Ví dụ 3 (SGK – tr 24)

Thực hành 3:

a) A∖B={0;1;2},B∖A={5},

(A∖B) $\cap $ (B∖A)=∅.
b) AB={3;4},

C$_{E}$(A $\cap $ B)={0;1;2;5;6;7}.

C$_{E}$A={5;6;7},

C$_{E}$B=0;1;2;6;7,

(C$_{E}$A) U (C$_{E}$B)={0;1;2;5;6;7}.

Nhận xét: C$_{E}$(A $\cap $ B)=(C$_{E}$A) U (C$_{E}$B).

c) A U B=0;1;2;3;4;5,

C$_{E}$(A U B)=6;7,

(C$_{E}$A) $\cap $ (C$_{E}$B)={6;7}.

Nhận xét: C$_{E}$(A U B)=(C$_{E}$A) $\cap $ (C$_{E}$B).

Ví dụ 4 (SGK – tr24)

Thực hành 4:
a) [-2;3)
b) [0;1)

c) [$\frac{1}{2}$;1]

d) (-∞;-1)