Bài tập 1. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy:

a. -2x + y - 1 $\leq$ 0;

b. -x + 2y > 0

c. x - 5y < 2;

d. -3x + y + 2 $\leq$ 0;

e. 3(X - 1) + 4(y - 2) < 5x - 3

Hướng dẫn giải:

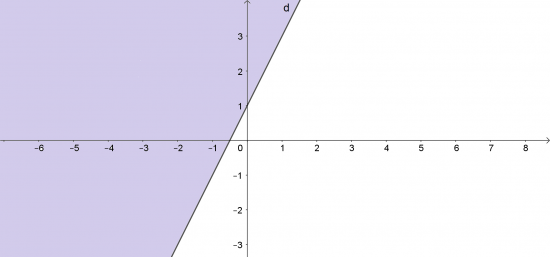
a. Vẽ đường thẳng d: -2x + y - 1 = 0 đi qua hai điểm (-$\frac{1}{2}$; 0) và (0; 1).

Xét gốc tọa độ O(0; 0) $\notin$ d và -2. 0 + 0 - 1 = -1 < 0 nên miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ d và chứa gốc tọa độ O.

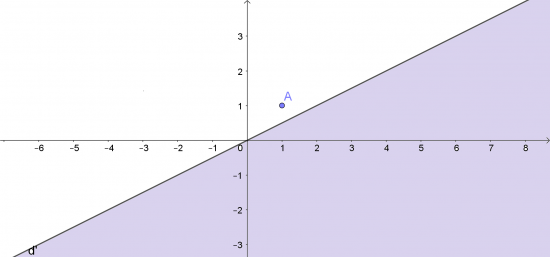
b. Vẽ đường thẳng d': -x + 2y = 0 đi qua gốc tọa độ O(0;0) và điểm (2, 1).

Xét điểm A(1; 1) $\notin$ d' và -1 + 2.1 = 1 > 0 nên miềm nghiệm của bất phương trình là nửa mặt phẳng không kể bờ d' và chứa điểm A.

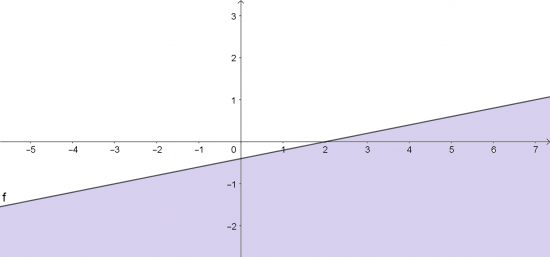
c. Vẽ đường thẳng f: x - 5y - 2 = 0 đi qua hai điểm (2; 0) và (0; -$\frac{5}{2}$.

Xét gốc tọa độ O(0;0). Ta thấy O $\notin$ f và 0 - 5. 0 - 2 = -2 < 0 nên miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ f và chứa gốc tọa độ O.

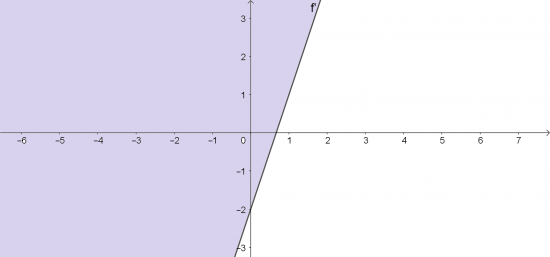
d. Vẽ đường thẳng f': -3x + y + 2 = 0 đi qua hai điểm ($\frac{2}{3}$; 0) và (0; -2).

Xét gốc tọa độ O(0; 0). Ta thấy O $\notin$ f' và -3. 0 + 0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ f' và không chứa gốc tọa độ O.

e. 3(x - 1) + 4(y - 2) < 5x - 3 <=> 3x - 3 + 4y - 8 < 5x - 3 <=> -2x + 4y -8 < 0 <=> x - 2y + 4 > 0

Vẽ đường thẳng t: x - 2y + 4 = 0 đi qua hai điểm (-4; 0) và (0; 2).

Xét gốc tọa độ O(0; 0). Ta thấy O $\notin$ t và 0 - 2. 0 + 4 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ t và chứa gốc tọa độ O.

Bài tập 2. Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy:

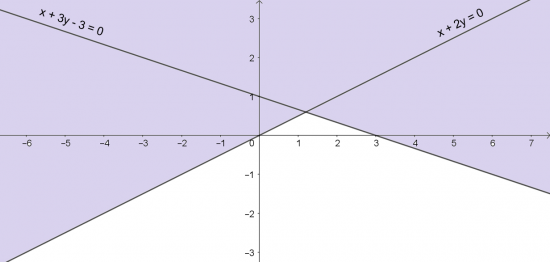
$\left\{\begin{matrix} x - 2y > 0\\ x + 3y < 3\end{matrix}\right.$

Hướng dẫn giải:

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.

Miền không tô màu( không kể bờ) là phần giao của hai miền nghiệm của hai bất phương trình và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.