1. GIÁ TRỊ LƯỢNG GIÁC

Khám phá 1: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn $\alpha$, lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = $\alpha$. Giả sử điểm M có tọa độ ($x_{0}$; $y_{0}$). Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

sin$\alpha$ = $y_{0}$; cos$\alpha$ = $x_{0}$; tan$\alpha$ = $\frac{y_{0}}{x_{0}}$; cot$\alpha$ = $\frac{x_{0}}{y_{0}}$

Hướng dẫn giải:

Xét tam giác OMH vuông tại H, ta có:

• sin$\alpha$ = $\frac{MH}{OM}$ = $\frac{y_{0}}{R}$ = $\frac{y_{0}}{1}$ = $y_{0}$
• cos$\alpha$ = $\frac{OH}{OM}$ = $\frac{x_{0}}{R}$ = $\frac{x_{0}}{1}$ = $x_{0}$
• tan$\alpha$ = $\frac{sin\alpha}{cos\alpha}$ = $\frac{y_{0}}{x_{0}}$
• cot$\alpha$ = $\frac{cos\alpha}{sin\alpha}$ = $\frac{x_{0}}{y_{0}}$

Thực hành 1: Tìm giá trị lượng giác góc $135^{\circ}$

Hướng dẫn giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = $135^{\circ}$. Ta có: $\widehat{MOy}$ = $135^{\circ}$ - $90^{\circ}$ = $45^{\circ}$.

Lại có: sin$45^{\circ}$ = $\frac{\sqrt{2}}{2}$; cos$45^{\circ}$ = $\frac{\sqrt{2}}{2}$ 

$\Rightarrow$ Tọa độ điểm M là $\left ( - \frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2} \right)$.

Vậy theo định nghĩa ta có: 

• sin$135^{\circ}$ = $\frac{\sqrt{2}}{2}$; cos$135^{\circ}$ = - $\frac{\sqrt{2}}{2}$
• tan$135^{\circ}$ = -1; cot$135^{\circ}$ = -1

2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU

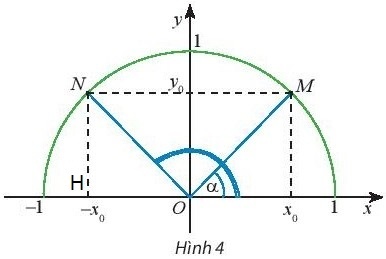
Khám phá 2: Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc $\widehat{xOM}$ và $\widehat{xON}$.

Hướng dẫn giải:

Gọi H là chân đường vuông góc hạ từ N xuống Ox.

Vì $\widehat{xOM}$ = $\widehat{HON}$ nên $\widehat{xOM}$ + $\widehat{xON}$ = $\widehat{HON}$ + $\widehat{xON}$ = $\widehat{HOx}$ = $180^{\circ}$

Thực hành 2: Tính các giá trị lượng giác: sin$120^{\circ}$; cos$150^{\circ}$, cot$135^{\circ}$

Hướng dẫn giải:

• sin$120^{\circ}$ = sin$(180^{\circ} - 60^{\circ})$ = $\frac{\sqrt{3}}{2}$ 
• cos$150^{\circ}$ = -cos$30^{\circ}$ = - $\frac{\sqrt{3}}{2}$ 
• cot$135^{\circ}$ = -cot$45^{\circ}$ = -1

Vận dụng 1: Cho biết sin$\alpha$ = $\frac{1}{2}$, tìm góc $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$) bằng cách vẽ nửa đường tròn đơn vị).

Hướng dẫn giải:

Theo định nghĩa, sin$\alpha$ = $y_{0}$ = $\frac{1}{2}$. Ta có hình vẽ:

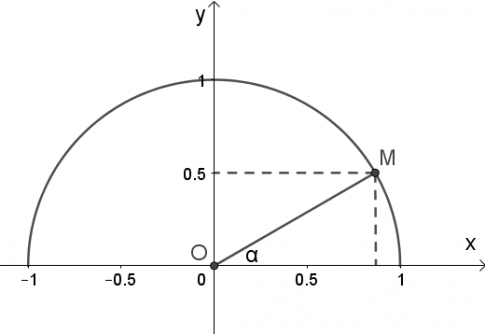
Đo $\alpha$ = $30^{\circ}$

3. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT

Thực hành 3: Tính:

A = sin$150^{\circ}$ + tan$135^{\circ}$ + cot$45^{\circ}$;

B = 2cos$30^{\circ}$ - 3tan$150^{\circ}$ + cot$135^{\circ}$

Hướng dẫn giải:

A = sin$150^{\circ}$ + tan$135^{\circ}$ + cot$45^{\circ}$

   = $\frac{1}{2}$ + (-1) + 1 = $\frac{1}{2}$

B = 2cos$30^{\circ}$ - 3tan$150^{\circ}$ + cot$135^{\circ}$

   = 2.$\frac{\sqrt{3}}{2}$ - 3.(- $\frac{\sqrt{3}}{3}$ + (-1) = -1 + 2$sqrt{3}

Vận dụng 2: Tìm góc $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$) trong mỗi trường hợp sau:

a. sin$\alpha$ = $\frac{\sqrt{3}}{2}$;

b. cos$\alpha$ = $\frac{-\sqrt{2}}{2}$;

c. tan$\alpha$ = -1;

d. cot$\alpha$ = -$sqrt{3}$

Hướng dẫn giải:

a. $\alpha$ =  $60^{\circ}$ hoặc $\alpha$ =  $120^{\circ}$

b. $\alpha$ =  $135^{\circ}$ 

c. $\alpha$ =  $135^{\circ}$

d. $\alpha$ =  $150^{\circ}$

4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC

Thực hành 4:

a. Tính cos$80^{\circ}$43'51''; tan$47^{\circ}$12'25''; cot$99^{\circ}$9'19''.

b. Tìm $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$), biết cos$\alpha$ = -0.723

Hướng dẫn giải:

a.

• cos$80^{\circ}$43'51'' $\approx$ 0,161
• tan$47^{\circ}$12'25'' $\approx$ 1,08
• cot$99^{\circ}$9'19'' $\approx$ -0,161

b. $\alpha$ $\approx$ $136^{\circ}$18'10''