CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC

BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0° ĐẾN 180°

1. GIÁ TRỊ LƯỢNG GIÁC

HĐKP 1:

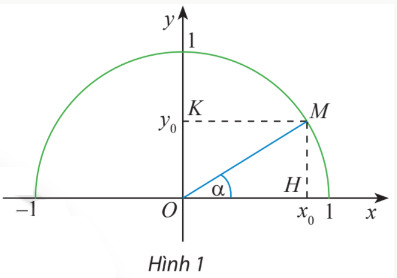
Ta có: Tam giác vuông OHM vuông tại H và $\alpha $ = $\widehat{xOM}$

Do đó: sin α = $\frac{MH}{OM}$; cos α = $\frac{OH}{OM}$

mà MH = y$_{0}$; OH = x$_{0}$; OM = 1

=> sin α = $\frac{y_{0}}{1}$ = y$_{0}$; cos α = $\frac{x_{0}}{1}$ = x$_{0}$

=> tan α = $\frac{sin α}{cos α}$ = $\frac{y_{0}}{x_{0}}$; cot α = $\frac{cos α}{sin α}$ = $\frac{x_{0}}{y_{0}}$

Định nghĩa:

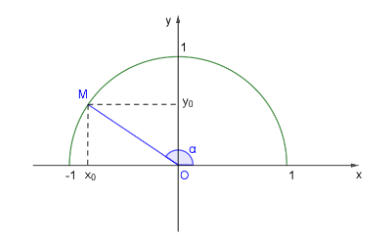
Với mỗi góc ( 0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = $\alpha $. Gọi (x0; y0) là tọa độ điểm M, ta có:

- Tung độ y$_{0}$ của M là sin của góc α, kí hiệu là sin α = y$_{0}$.

- Hoành độ x$_{0}$ của M là côsin của góc α, kí hiệu là cos α = x$_{0}$;

- Tỉ số  $\frac{y_{0}}{x_{0}}$ (x$_{0}$ ≠ 0) là tang của góc α, kí hiệu là tan α = $\frac{y_{0}}{x_{0}}$ ;

- Tỉ số $\frac{x_{0}}{y_{0}}$ (y$_{0}$ ≠ 0) là cô tang của góc α, kí hiệu là cot α= $\frac{x_{0}}{y_{0}}$.

Chú ý:

tan α = $\frac{sin α}{cos α}$ (α≠90$^{\circ}$);

cot α = $\frac{cos α}{sin α}$ (α≠0$^{\circ}$ và α≠180$^{\circ}$);

tan α =$\frac{1}{cot α}$ (α∉{0$^{\circ}$ 90$^{\circ}$ 180$^{\circ}$})

Ví dụ 1 (SGK - tr62)

Chú ý:

a) Nếu là góc nhọn thì các giá trị lượng giác của đều dương.

Nếu là góc tù thì sin α> 0, cos α< 0, tan α< 0, cot α< 0.

b) tan chỉ xác định khi α ≠ 90°.

tan chỉ xác định khi α ≠ 0° và α ≠ 180°.

Thực hành 1:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = 135°, H là hình chiếu vuông góc của M trên Oy.

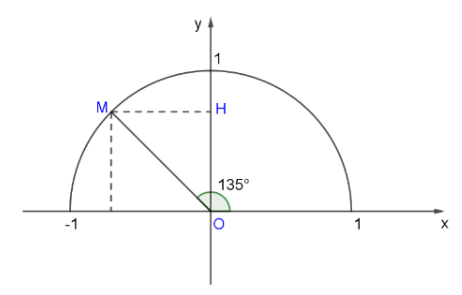
Ta có: $\widehat{MOy}$ = 135° - 90° = 45°.

Tam giác OMH vuông cân tại H nên OH = MH = $\frac{OM}{\sqrt{2}}$=$\frac{1}{\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$.

Tọa độ điểm M là (-$\frac{\sqrt{2}}{2}$; $\frac{\sqrt{2}}{2}$)

Vậy theo định nghĩa ta có:

sin135° =$\frac{\sqrt{2}}{2}$; cos135° = -$\frac{\sqrt{2}}{2}$;

tan135° = -1; cot135° = -1

2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU 

HĐKP 2: 

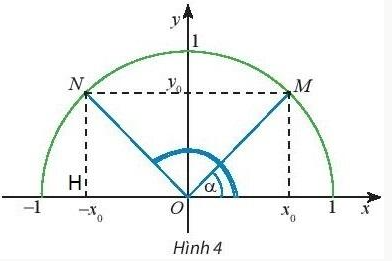
Gọi H là chân đường vuông góc hạ từ N xuống Ox.

Ta có: $\widehat{NOH}$ = $\widehat{ONM}$ =$\widehat{OMN}$ = $\widehat{MOx}$ = (do NM // Ox)

mà $\widehat{xON}$ + $\widehat{NOH}$ = 180° 

⟹ $\widehat{xON}$ + $\widehat{xOM}$ = 180°

Kết luận:

Với mọi góc thỏa mãn 0° ≤ α ≤ 180°, ta luôn có:

sin(180° - α) = sin α;

cos(180° - α) = - cos α;

tan(180° - α) = - tan α ( α≠ 90°)

cot(180° - α) = - cot α (0° < α < 180°)

Ví dụ 2 (SGK - tr63)

Thực hành 2:

sin120° = sin(180° - 60°) = sin60° = $\frac{\sqrt{3}}{2}$

cos150° = -cos(180° - 30°) = -cos30° = -$\frac{\sqrt{3}}{2}$

cot135° = -cot(180° - 45°) = - cot45° = -1.

Vận dụng 1:

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: $\widehat{xOM}$ = α .

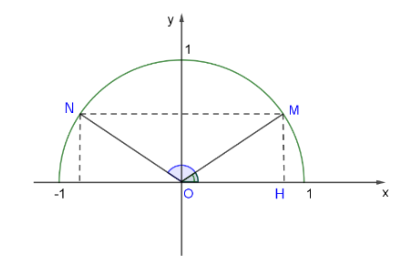
Do sin α = $\frac{1}{2}$ nên tung độ của M bằng $\frac{1}{2}$. Vậy ta xác định được hai điểm N và M trên nửa đường tròn đơn vị, thỏa mãn sin $\widehat{xON}$ = sin$\widehat{xOM}$ = $\frac{1}{2}$.

Đặt α  = $\widehat{xOM}$ ⟹$\widehat{xON}$ = 180° - α

Xét tam giác OHM vuông tại H ta có:

sin α= $\frac{MH}{OM}$=$\frac{1}{2}$ => α =30$^{\circ}$=$\widehat{xOM}$

⟹ $\widehat{xON}$ = 180° - 30° = 150°.

Vậy α = 30° hoặc α = 150°

3. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT 

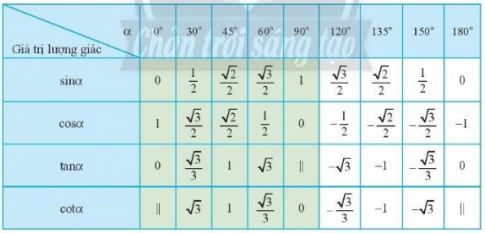
Thực hành 3: 

A = sin150° + tan135° + cot45°

    = $\frac{1}{2}$ + (-1) + 1 = $\frac{1}{2}$

B = 2cos30° - 3tan150° + cot135°

   = 2. $\frac{\sqrt{3}}{2}$ - 3. (-$\frac{\sqrt{3}}{3}$) + (-1) = 2$\sqrt{3}$ - 1

Vận dụng 2:

a) = 60° hoặc = 120°

b) = 135°

c) = 135°

d) = 150°

4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC 

a) Tính các giá trị lượng giác của góc

Ví dụ 3 (SGK - tr64)

b) Xác định số đo của góc khi biết giá trị lượng giác của góc đó.

Ví dụ 4 (SGK - tr64)

Thực hành 4:

a) cos80°43'51'' ≈ 0,161

    tan47°12'25'' ≈ 1,08

    cot99°9'19'' ≈ -0,161

b) α ≈ 136°18'10''