BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ -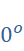

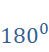
1. GIÁ TRỊ LƯỢNG GIÁC

Bài 1: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho = α. Giả sử điểm M có tọa độ (). Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

sinα = ; cosα = ; tanα = ; cotα =  

Giải nhanh: 

Ta có: Tam giác vuông OHM vuông tại H và =

Do đó: sin = ; cos =

mà MH = y₀; OH = x₀; OM = 1

sin = y₀; cos = x₀

tan = ; cot = 

Bài 2: Tìm giá trị lượng giác góc 135

Giải nhanh:

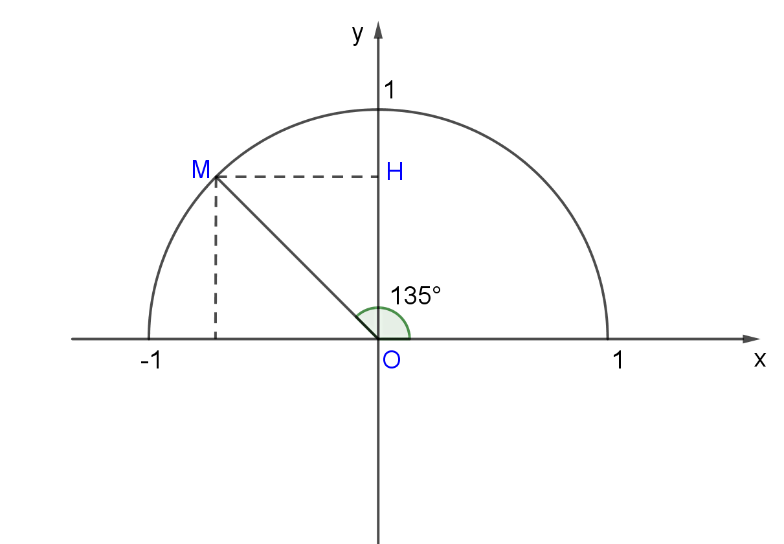
Ta có: = 135 - 90 = 45.

Tam giác OMH vuông cân tại H nên OH = MH = = .

Tọa độ điểm M là

Vậy theo định nghĩa ta có:

sin135 = ; cos135 = ;

tan135 = -1; cot135 = -1

2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU

Bài 1: Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc  và .

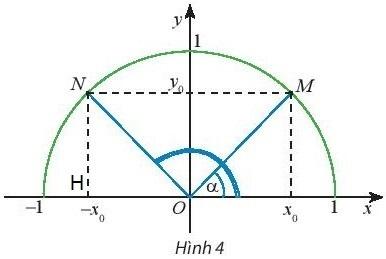
Giải nhanh: 

Gọi H là chân đường vuông góc hạ từ N xuống Ox.

Ta có: = = = = (do NM // Ox)

mà + = 180 + = 180

Bài 2: Tính các giá trị lượng giác: sin120; cos150, cot135

Giải nhanh: 

sin120 = sin60 =

cos150 = -cos30 = -

cot135 = - cot45 = -1

Bài 3: Cho biết sinα = , tìm góc α (0≤ α ≤180) bằng cách vẽ nửa đường tròn đơn vị).

Giải nhanh: 

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: = .

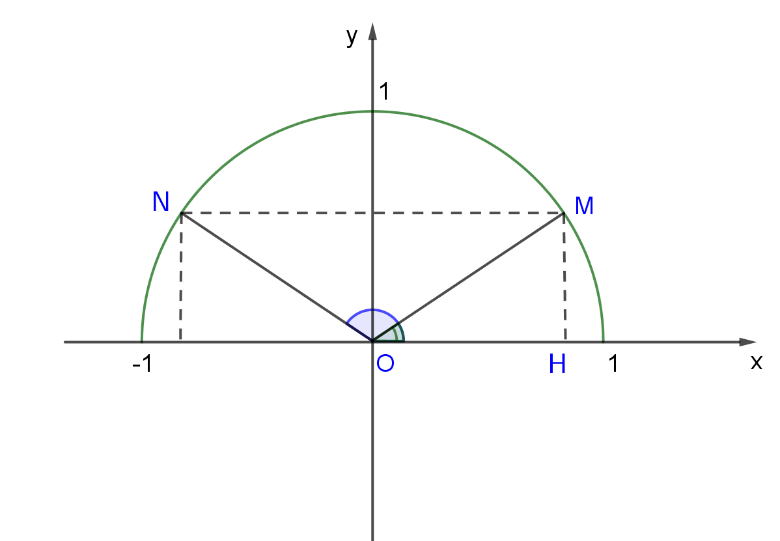
Do sin = nên tung độ của M bằng . Vậy ta xác định được hai điểm N và M trên nửa đường tròn đơn vị, thỏa mãn sin = sin = .

Đặt = = 180 -

Xét tam giác OHM vuông tại H ta có:

= 150

Vậy = 30 hoặc = 150

3. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT

Bài 1: Tính:

A = sin150 + tan135 + cot45

B = 2cos30 - 3tan150 + cot135

Giải nhanh: 

A =

B = 2 - 1

Bài 2: Tìm góc α (0≤ α ≤180) trong mỗi trường hợp sau:

a. sinα =

b. cosα =

c. tanα = -1

d. cotα = -

Giải nhanh: 

a) = 60 hoặc = 120

b) = 135

c) = 135

d) = 150

4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC

Bài 1: 

1. Tính cos8043'51'' ; tan4712'25'' ; cot 99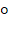9'19'' 

2. Tìm α (0≤ α ≤ 180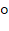), biết cosα = -0.723

Giải nhanh: 

a) cos8043'51'' ≈ 0,161

    tan4712'25'' ≈ 1,08

    cot999'19'' ≈ -0,161

b) 13618'10''

BÀI TẬP CUỐI SGK

Bài 1. Cho biết sin30 = ; sin60 = ; tan45 = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30 + sin150 + tan135

Giải nhanh: 

E =

Bài 2. Chứng minh rằng:

a)

b)

Giải nhanh: 

a)

b) suy ra

Bài 3. Tìm góc α (0≤α≤180) trong mỗi trường hợp sau:

a. cosα = -

b. sinα = 0;

c. tanα = 1;

d. cotα không xác định.

Giải nhanh: 
a) ;
b) hoặc ;
c)
d) không xác định khi hoặc .

Bài 4. Cho tam giác ABC. Chứng minh rằng:

a. sinA = sin(B + C)

b. cosA = cos(B + C)

Giải nhanh: 
a)
b)

Bài 5. Chứng minh rằng với mọi góc α (0≤ α ≤180), ta đều có:

a. α +α = 1

b. tanα. cotα = 1 (0<α<180, α ≠ 90)

c. 1 + α  =

d. 1 + α  = (0<α<180, α ≠ 90)

Giải nhanh: 

a) 

b)

c)

d)

Bài 6. Cho góc α với cosα = −  . Tính giá trị của biểu thức A = 2α + 5α

Giải nhanh: 

Bài 7. Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:

a. Tính ;;;

b. Tìm α (0≤α≤180) trong các trường hợp sau:

i. sinα = 0,862;        ii. cosα = - 0,567;            iii. tanα = 0,334 

Giải nhanh: 

a)

; 

.

b) 

i) hoặc ;

ii)

iii)