BÀI TẬP CUỐI CHƯƠNG 6

Bài 1. Một hàng số quan trong trong toán học là số e có giá trị gần đúng với 12 chữ số thập phân là 2,718281828459.

a. Giả sử ta lấy giá trị 2,7 làm giá trị gần đúng của e. Hãy chứng tỏ sai số tuyệt đối không vượt quá 0,02 và sai số tương đối không vượt quá 0,75$.

b. Hãy quy tròn e đến hàng phần nghìn.

c. Tìm số gần đúng của số e với độ chính xác 0,00002.

Giải nhanh: 

a) = | - e| < 0,02

0,75%

b) e = 2,718

c) 2,7183

Bài 2. Cho các số gần đúng a = 54919020 ± 1000 và b = 5,7914003 ± 0,002.

Hãy xác định số quy tròn của a và b.

Giải nhanh: 

a: 54920000

b: 5,79

Bài 3. Mỗi học sinh lớp 10A đóng góp 2 quyển sách cho thư viện trường. Lớp trưởng thống kê lại số sách mỗi tổ trong lớp đóng góp ở bảng sau:

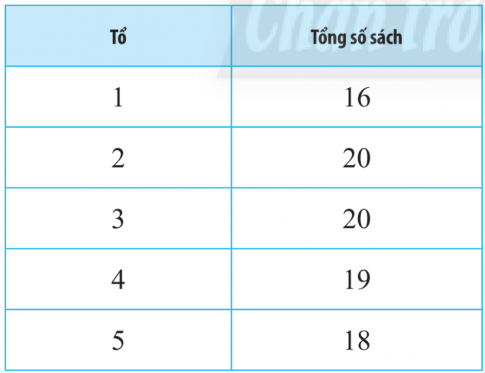
Hãy cho biết lớp trưởng đã thống kê chính xác chưa? Tại sao?

Giải nhanh: 

Lớp trưởng thống kê chưa chính xác.

Bài 4. Sản lượng nuôi tôm phân theo địa phương của các tỉnh Cà Mau và Tiền Giang được thể hiện ở hai biểu đồ sau (đơn vị: tấn):

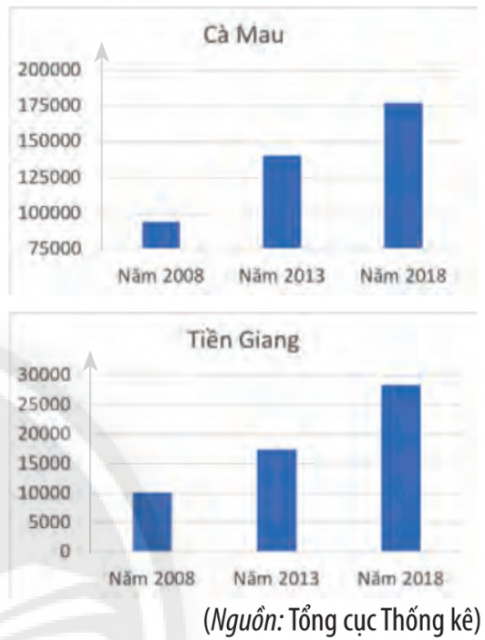
a. Hãy cho biết các phát biểu sau là đúng hay sai:

(i)Sản lượng nuôi tôm mỗi năm của tỉnh Tiền Giang đều cao hơn tỉnh Cà Mau.
(ii) Ở tỉnh Cà Mau, sản lượng nuôi tôm năm 2018 tăng gấp hơn 4 lần so với năm 2008.
(iii) Ở tỉnh Tiền Giang, sản lượng nuôi tôm năm 2018 tăng gấp hơn 2,5 lần so với năm 2008.
(iv) Ở tỉnh Tiền Giang, từ năm 2008 đến năm 2018, sản lượng nuôi tôm mỗi năm tăng trên 50% so với năm cũ.
(v) Trong vòng 5 năm từ 2013 đến 2018, sản lượng nuôi tôm của tỉnh Cà Mau tăng cao hơn của tỉnh Tiền Giang.

b. Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ nào?

Giải nhanh: 

a. Khẳng định (i) sai.

Khẳng định (ii) sai.

Khẳng định (iii) đúng.

Khẳng định (iv) sai.

Khẳng định (v) đúng.

b. Biểu đồ cột kép

Bài 5. Bạn Châu cần lần lượt 50 quả vải thiều Thanh Hà được lựa chọn ngẫu nhiên từ vườn nhà mình và được kết quả như sau:

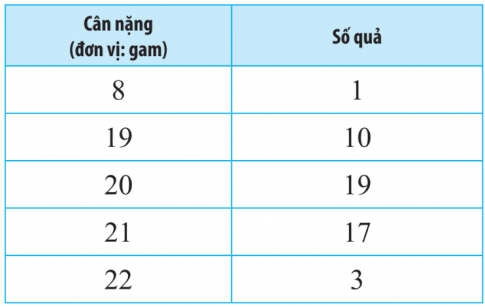
a. Hãy tìm số trung bình, trung vị, mốt của mẫu số liệu trên.

b. Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ của mẫu số liệu trên.

Giải nhanh: 

a) = 20,02 (g)

= (20 + 20) = 20.

= 20.

b) S = 1,91

R = 22 - 8 = 14

= 20

= 20.

= 21

= - = 21 - 20 = 1.

Ta có: + 1,5. = 21 + 1,5.1 = 22,5; - 1,5. = 20 - 1,5. 1 = 18,5.

Vậy 8 là giá trị ngoại lệ của mẫu số liệu trên.

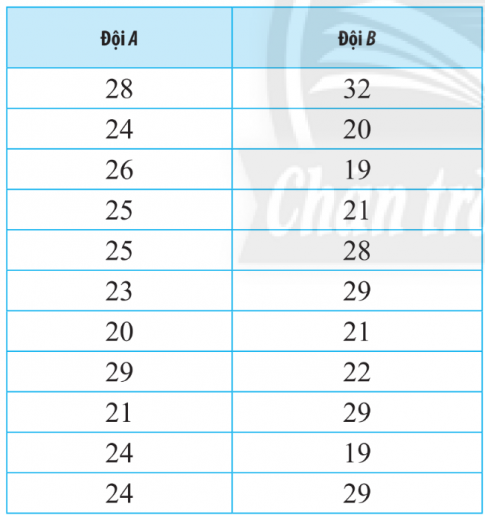
Bài 6. Độ tuổi của 22 cầu thủ ở đội hình xuất phát của hai đội bóng đá được ghi lại ở bảng sau:

a. Hãy tìm số trung bình, mốt, độ lệch chuẩn và tứ phân bị của tuổi mỗi cầu thủ của từng đội bóng.

b. Tuổi của các cầu thủ ở đội bóng nào đồng đều hơn? Tại sao?

Giải nhanh: 

a) 24,4545

24,4545

2,54

4,68

Sắp xếp số tuổi của các cầu thủ ở đội bóng A theo thứ tự không giảm, ta được: 

20; 21; 23; 24; 24; 24; 25; 25; 26; 28; 29.

= 24.

= 24.

= 23

= 26.

Sắp xếp số tuổi của các cầu thủ ở đội bóng B theo thứ tự không giảm, ta được: 19; 19; 20; 21; 21; 22; 28; 29; 29; 29; 32.

= 29.

= 22.

= 20

= 29.

b) Nhận thấy độ lệch chuẩn của tuổi mỗi cầu thủ ở đội bóng A nhỏ hơn độ lệch chuẩn của tuổi mỗi cầu thủ ở đội bóng B nên độ tuổi của các cầu thủ ở đội B có độ phân tán cao hơn đội A. Do đó, tuổi của các cầu thủ ở đội A đồng đều hơn.

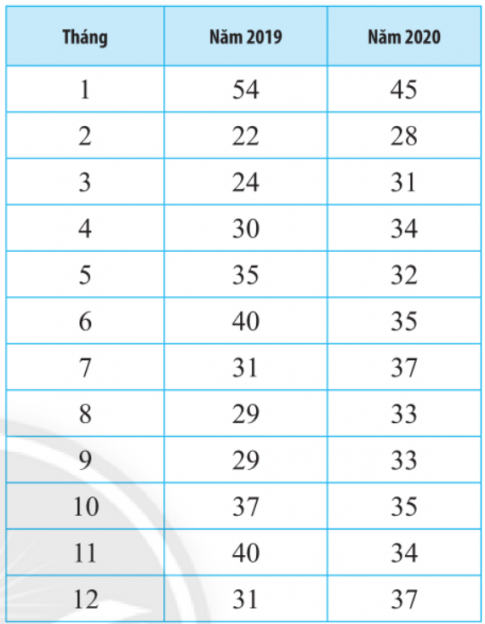
Bài 7. Một cửa hàng bán xe ô tô thay đổi chiến lược kinh doanh vào cuối năm 2019. Số xe cửa hàng bán được mỗi tháng trong năm 2019 và 2020 được ghi lại ở bảng sau:

a. Hãy tính số trung bình, khoảng tứ phân vị và độ lệch chuẩn của số lượng xe bán được trong năm 2019 và năm 2020.

b. Nêu nhận xét về tác động của chiến lược kinh doanh mới lên số lượng xe bán ra hàng tháng.

Giải nhanh: 

a) Năm 2019

Số lượng xe trung bình bán được là:

= (54 + 22 + 24 + 30 + 35 + 40 + 31 + 29 + 29 + 37 + 40 + 31) = 33,5

Độ lệch chuẩn của số lượng xe bán được là:

=

8,2

Sắp xếp số lượng xe bán được theo thứ tự không giảm, ta được: 22; 24; 29; 29; 30; 31; 31; 35; 37; 40; 40; 54.

= 31

= 29

= (37 + 40) = 38,5

= 38,5 - 29 = 9,5.

Năm 2020:

Số lượng xe trung bình bán được là:

= (45 + 28 + 31 + 34 + 32 + 35 + 37 + 33 + 33 + 35 +34 + 37) = 34,5

Độ lệch chuẩn của số lượng xe bán được là:

=

3,97

Sắp xếp số lượng xe bán được trong năm 2020 theo thứ tự không giảm, ta được: 28; 31; 32; 33; 33; 34; 34; 35; 35; 37; 37; 45.

= 34

= 32,5

= 36

= 36 - 32,5 = 3,5.

b) Nhận thấy độ lệch chuẩn của số lượng xe bán được trong năm 2020 nhỏ hơn độ lệch chuẩn của số lượng xe bán được trong năm 2019; số lượng xe trung bình bán ra trong năm 2020 cao hơn năm 2019. Do đó, chiến lược kinh doanh mới đã giúp lượng xe bán ra hàng tháng trong năm 2020 ổn định và nhiều hơn so với năm 2019.