1. GÓC GIỮA HAI VECTƠ

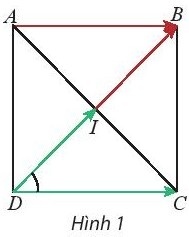
Khám phá 1: Cho hình vuông ABCD có tâm I (Hình 1).

a. Tính $\widehat{IDC}$.

b. Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C.

c. Tìm hai vectơ cùng có điểm đầu là D và lần lượt bằng vectơ $\vec{IB}$ và $\vec{AB}$.

Hướng dẫn giải:

a. $\widehat{DIC}$ = $45^{\circ}$

b. Hai vectơ cần tìm là $\vec{DI}$ và $\vec{DC}$

c. $\vec{DI}$ = $\vec{IB}$; $\vec{DC}$ = $\vec{AB}$

Thực hành 1: Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc: ($\vec{AB}$, $\vec{AC}$), ($\vec{AB}$, $\vec{BC}$), ($\vec{AH}$, $\vec{BC}$), ($\vec{BH}$, $\vec{BC}$), ($\vec{HB}$, $\vec{BC}$)

Hướng dẫn giải:

Lấy điểm D sao cho AD // BC và AD = BC

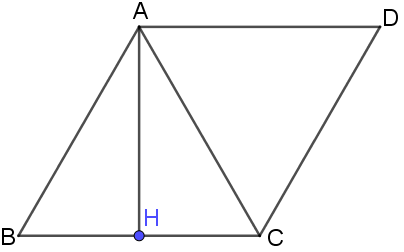
• ($\vec{AB}$, $\vec{AC}$) = $\widehat{BAC} = 60^{\circ}$
• ($\vec{AB}$, $\vec{BC}$) = ($\vec{AB}$, $\vec{AD}$) = $\widehat{BAD} = 120^{\circ}$
• ($\vec{AH}$, $\vec{BC}$) = ($\vec{AH}$, $\vec{AD}$) = $\widehat{HAD} = 90^{\circ}$

Do hai vectơ $\vec{BH}$ và $\vec{BC}$ cùng hướng nên ($\vec{BH}$, $\vec{BC}$) = $0^{\circ}$

Do hai vectơ $\vec{HB}$ và $\vec{BC}$ ngược hướng nên ($\vec{HB}$, $\vec{BC}$) = $180^{\circ}$.

2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

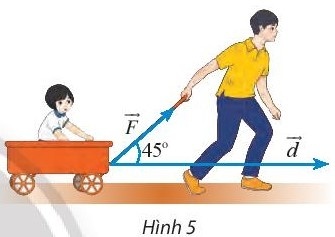
Khám phá 2: Một người dùng một lực $\vec{F}$ có cường độ 10N kéo một chiếc xe đi quãng đường dài 100m. Tính công sinh bởi lực $\vec{F}$, biết rằng góc giữa vectơ $\vec{F}$ và hướng di chuyển là $45^{\circ}$. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực $\vec{F}$, độ dài  quãng đường và côsin của góc giữa hai $\vec{F}$ và độ dịch chuyển $\vec{d}$).

Hướng dẫn giải:

A = |$\vec{F}$|.|$\vec{d}$|.$cos45^{\circ}$ = 10. 100.$cos45^{\circ}$ = $500\sqrt{2}$ (J)

Thực hành 2: Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng $\sqrt{2}$. Tính các tích vô hướng: $\vec{AB}$. $\vec{AC}$, $\vec{AC}$. $\vec{BC}$, $\vec{BA}$. $\vec{BC}$

Hướng dẫn giải:

Tam giác ABC vuông cân tại A có BC = $\sqrt{2}$ $\Rightarrow$ AB = AC = 1

$\vec{AB}$. $\vec{AC}$ = |$\vec{AB}$|. |$\vec{AC}$|.cos($\vec{AB}$, $\vec{AC}$) = 1. 1. cos$90^{\circ}$ = 0

$\vec{AC}$.$\vec{BC}$ = |$\vec{AC}$|. |$\vec{BC}$|. cos($\vec{AC}$, $\vec{BC}$) = 1. $\sqrt{2}$. cos$45^{\circ}$ = 1

$\vec{BA}$.$\vec{BC}$ = |$\vec{BA}$|.|$\vec{BC}$|.cos($\vec{BA}$, $\vec{BC}$) = 1. $\sqrt{2}$. cos$45^{\circ}$ = 1

Thực hành 3: Hai vectơ $\vec{a}$ và $\vec{b}$ có độ dài lần lượt là 3 và 8 và có tích vô hướng là $12\sqrt{2}$. Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$.

Hướng dẫn giải:

Ta có: cos($\vec{a}$, $\vec{b)}$ = $\frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|}$ = $\frac{12\sqrt{2}}{3. 8}$ = $\frac{\sqrt{2}}{2}$

$\Rightarrow$ ($\vec{a}$, $\vec{b}$) = $45^{\circ}$

Vận dụng 1: Một người dùng một lực $\vec{F}$ có độ lớn là 20N kéo một vật dịch chuyển một đoạn 50m cùng hướng với $\vec{F}$. Tính công sinh bởi lực $\vec{F}$.

Hướng dẫn giải:

A = 20. 50. $cos0^{\circ}$ = 1000 (J)

3. TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG

Thực hành 4: Cho hai vectơ $\vec{i}$, $\vec{j}$ vuông góc, cùng có độ dài bằng 1.

a. Tính $(\vec{i} + \vec{j})^{2}$, $(\vec{i} - \vec{j})^{2}$, ($\vec{i}$ + $\vec{j}$).($\vec{i}$ - $\vec{j}$)

b. Cho $\vec{a}$ = 2$\vec{i}$ + 2$\vec{j}$, b = 3$\vec{i}$ - 3$\vec{j}$. Tính tích vô hướng $\vec{a}$.$\vec{b}$ và tính góc ($\vec{a}$, $\vec{b}$)

Hướng dẫn giải:

a. $(\vec{i} + \vec{j})^{2}$ = $\vec{i}^{2}$ + 2$\vec{i}$. $\vec{j}$ + $\vec{j}^{2}$ = $|\vec{i}|^{2}$ + $|\vec{j}|^{2}$ + 2.|$\vec{i}$|. |$\vec{j}$|. cos$90^{\circ}$ = $1^{2}$ + $1^{2}$ + 0 = 2

$(\vec{i} - \vec{j})^{2}$ = $\vec{i}^{2}$ - 2$\vec{i}$. $\vec{j}$ + $\vec{j}^{2}$ = $|\vec{i}|^{2}$ + $|\vec{j}|^{2}$ - 2.|$\vec{i}$|. |$\vec{j}$|. cos$90^{\circ}$ = $1^{2}$ + $1^{2}$ - 0 = 2

($\vec{i}$ + $\vec{j}$).($\vec{i}$ - $\vec{j}$) = $\vec{i}^{2}$ - $\vec{j}^{2}$ = $|\vec{i}|^{2}$ - $|\vec{j}|^{2}$ = $1^{2}$ - $1^{2}$ = 0

b. Ta có: $\vec{a}$. $\vec{b}$ = (2$\vec{i}$ + 2$\vec{j}$)(3$\vec{i}$ - 3$\vec{j}$) = 6($\vec{i}$ + $\vec{j}$)($\vec{i}$ - $\vec{j}$) = 6. 0 = 0

$\Rightarrow$ ($\vec{a}$; $\vec{b}$) = $90^{\circ}$

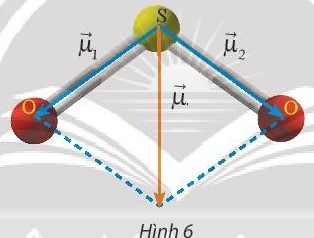
Vận dụng 2: Phân tử sulfur dioxide ($SO_{2}$) có cấu tạo hình chữ V, góc liên kết $\widehat{OSO}$ gần bằng $120^{\circ}$. Người ta biểu diễn sự phân cực giữa nguyên tử S với mỗi nguyên tử O bằng các vectơ $\vec{\mu_{1}}$ và $\vec{\mu_{2}}$ có cùng phương liên kết công hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có cùng độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng $\vec{\mu}$ = $\vec{\mu_{1}}$ + $\vec{\mu_{2}}$ được dùng để biểu diễn sự phân cực của cả phân tử $SO_{2}$. Tính độ dài của $\vec{\mu}$.

Hướng dẫn giải:

|$\vec{\mu}$| $\approx \sqrt{1,6^{2} + 1,6^{2} + 2.1,6, 1,6.cos120^{\circ}}$ = 1,6