CHƯƠNG V. VECTƠ

BÀI 4. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

1. GÓC GIỮA HAI VECTƠ

HĐKP1:

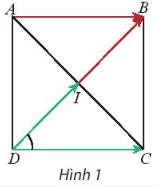
a) $\widehat{IDC}$ = 45°

b) Hai vectơ cần tìm là DI và DC

c) $\underset{DI}{\rightarrow}$ =$\underset{IB}{\rightarrow}$;  $\underset{DC}{\rightarrow}$ = $\underset{AB}{\rightarrow}$

Kết luận:

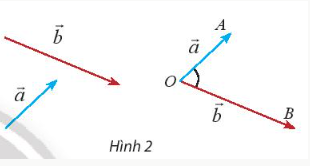
Cho hai vectơ $\underset{a}{\rightarrow}$ khác $\underset{b}{\rightarrow}$ khác $\underset{0}{\rightarrow}$. Từ một điểm O bất kì ta vẽ $\underset{OA}{\rightarrow}$=$\underset{a}{\rightarrow}$; $\underset{OB}{\rightarrow}$= $\underset{b}{\rightarrow}$ 

Góc AOB với số đo từ 0$^{\circ}$ đến 180$^{\circ}$ được gọi là góc giữa hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$.

Ta kí hiệu góc giữa hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ là ($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$).

Nếu ($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$) = 90$^{\circ}$ thì ta nói rằng $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ vuông góc với nhau, kí hiệu $\underset{a}{\rightarrow}$ ⊥ $\underset{b}{\rightarrow}$.

* Chú ý:

- Từ định nghĩa ta có: ($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$) = ($\underset{b}{\rightarrow}$,$\underset{a}{\rightarrow}$ )

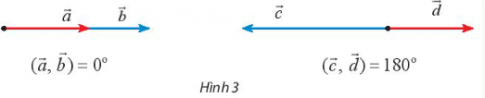
- Góc giữa hai vectơ ngược hướng và khác $\underset{0}{\rightarrow}$ luôn bằng 180$^{\circ}$.

- Trong trường hợp có ít nhất một trong hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ là vectơ 

Ví dụ 1: SGK-tr98

Thực hành 1.

Lấy điểm D sao cho AD // BC và AD = BC

($\underset{AB}{\rightarrow}$, $\underset{AC}{\rightarrow}$) = $\widehat{BAC}$=60°

($\underset{AB}{\rightarrow}$, $\underset{BC}{\rightarrow}$) = ($\underset{AB}{\rightarrow}$, $\underset{AD}{\rightarrow}$) = $\widehat{BAD}$=120°

($\underset{AH}{\rightarrow}$, $\underset{BC}{\rightarrow}$) = ($\underset{AH}{\rightarrow}$, $\underset{AD}{\rightarrow}$) = $\widehat{HAD}$=90°

Do hai vectơ $\underset{BH}{\rightarrow}$ và $\underset{BC}{\rightarrow}$ cùng hướng nên ($\underset{BH}{\rightarrow}$, $\underset{BC}{\rightarrow}$) = 0°

Do hai vectơ $\underset{HB}{\rightarrow}$ và $\underset{BC}{\rightarrow}$ ngược hướng nên ($\underset{HB}{\rightarrow}$, $\underset{BC}{\rightarrow}$) = 180°.

2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

A = |$\underset{F}{\rightarrow}$|.|$\underset{d}{\rightarrow}$|.cos45°=10.100.cos45° 

= 500$\sqrt{2}$ (J)

⇒ Kết luận:

Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ đều khác $\underset{0}{\rightarrow}$ .

Tích vô hướng của $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ là một số, kí hiệu là $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$, được xác định bởi công thức:

$\underset{a}{\rightarrow}$.$\underset{b}{\rightarrow}$=|$\underset{a}{\rightarrow}$|. |$\underset{b}{\rightarrow}$|.cos($\underset{a}{\rightarrow}$,$\underset{b}{\rightarrow}$).

* Chú ý:

a) Trường hợp ít nhất một trong hai vectơ 

$\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ bằng $\underset{0}{\rightarrow}$, ta quy ước $\underset{a}{\rightarrow}$.$\underset{b}{\rightarrow}$ = $\underset{0}{\rightarrow}$

b) Với hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$, ta có $\underset{a}{\rightarrow} \perp  \underset{b}{\rightarrow}$

⟺ $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ = 0.

c) Khi $\underset{a}{\rightarrow}$ = $\underset{b}{\rightarrow}$ thì tích vô hướng $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ được kí hiệu là $\underset{a^{2}}{\rightarrow}$. Vậy bình phương vô hướng của một vectơ luôn bằng bình phương của độ dài của vectơ đó.

Ví dụ 2: SGK – tr99,100.

* Chú ý:

Trong Vật lí, tích vô hướng của $\underset{F}{\rightarrow}$ và $\underset{d}{\rightarrow}$ biểu diễn công A sinh bởi lực $\underset{F}{\rightarrow}$ khi thực hiện độ dịch chuyển $\underset{d}{\rightarrow}$. Ta có công thức: A = $\underset{F}{\rightarrow}$.$\underset{d}{\rightarrow}$.

Thực hành 2.

Tam giác ABC vuông cân tại A có BC = $\sqrt{2}$ =>  AB = AC = 1

$\underset{AB}{\rightarrow}$. $\underset{AC}{\rightarrow}$ = |$\underset{AB}{\rightarrow}$|. |$\underset{AC}{\rightarrow}$|.cos($\underset{AB}{\rightarrow}$, $\underset{AC}{\rightarrow}$) = 1. 1. cos90° = 0

$\underset{AC}{\rightarrow}$.$\underset{BC}{\rightarrow}$ = |$\underset{AC}{\rightarrow}$|. |$\underset{BC}{\rightarrow}$|. cos($\underset{AC}{\rightarrow}$, $\underset{BC}{\rightarrow}$) = 1. $\sqrt{2}$. cos45° = 1

$\underset{BA}{\rightarrow}$.$\underset{BC}{\rightarrow}$ = |$\underset{BA}{\rightarrow}$|.|$\underset{BC}{\rightarrow}$|.cos($\underset{BA}{\rightarrow}$,$\underset{BC}{\rightarrow}$) = 1. $\sqrt{2}$. cos45° = 1

Thực hành 3.

Ta có: cos($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$) = $\frac{\underset{a}{\rightarrow}.\underset{b}{\rightarrow}}{\left | \underset{a}{\rightarrow} \right |.\left | \underset{b}{\rightarrow} \right |}$= $\frac{12\sqrt{2}}{3.8}$=$\frac{\sqrt{2}}{2}$

=> ($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$)=45°

Vận dụng 1.

A = 20. 50. cos0° = 1000 (J)

3. TÍNH CHẤT TÍCH VÔ HƯỚNG.

Tính chất:

Với ba vectơ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$, $\underset{c}{\rightarrow}$ bất kì và mọi số k, ta có:

$\underset{a}{\rightarrow}$.$\underset{b}{\rightarrow}$ =$\underset{b}{\rightarrow}$.$\underset{a}{\rightarrow}$

$\underset{a}{\rightarrow}$.($\underset{b}{\rightarrow}$+$\underset{c}{\rightarrow}$) = $\underset{a}{\rightarrow}$.$\underset{b}{\rightarrow}$ + $\underset{a}{\rightarrow}$.$\underset{c}{\rightarrow}$

(k.$\underset{a}{\rightarrow}$) . $\underset{b}{\rightarrow}$ = k. ($\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$) = $\underset{a}{\rightarrow}$ .(k.$\underset{b}{\rightarrow}$) 

Ví dụ 3: SGK-tr100

* Nhận xét: Chứng minh tương tự, ta cũng có:

($\underset{a}{\rightarrow}$ - $\underset{b}{\rightarrow}$)$^{2}$ = $\underset{a}{\rightarrow}^{2}$ - 2$\underset{a}{\rightarrow}$.$\underset{b}{\rightarrow}$ + $\underset{b}{\rightarrow}^{2}$

($\underset{a}{\rightarrow}$ - $\underset{b}{\rightarrow}$).($\underset{a}{\rightarrow}$ + $\underset{b}{\rightarrow}$) =$\underset{a}{\rightarrow}^{2}$ - $\underset{b}{\rightarrow}^{2}$

Ví dụ 4: SGK – tr101

Thực hành 4.

a) ($\underset{i}{\rightarrow}$+$\underset{j}{\rightarrow}$)$^{2}$= $\underset{i}{\rightarrow}^{2}$ + 2$\underset{i}{\rightarrow}$. $\underset{j}{\rightarrow}$ + $\underset{j}{\rightarrow}^{2}$ = |$\underset{i}{\rightarrow}$|$^{2}$ + |$\underset{j}{\rightarrow}$|$^{2}$ + 2.|$\underset{i}{\rightarrow}$|. |$\underset{j}{\rightarrow}$|. cos90° = 1$^{2}$ + 1$^{2}$ + 0 = 2

($\underset{i}{\rightarrow}$-$\underset{j}{\rightarrow}$)$^{2}$ = $\underset{i}{\rightarrow}^{2}$ - 2. $\underset{i}{\rightarrow}$ + $\underset{i}{\rightarrow}^{2}$ = |$\underset{i}{\rightarrow}$|$^{2}$ + |$\underset{j}{\rightarrow}$|$^{2}$ - 2.|$\underset{i}{\rightarrow}$|. |$\underset{j}{\rightarrow}$|. cos90° = 1$^{2}$ + 1$^{2}$ - 0 = 2

($\underset{i}{\rightarrow}$ + $\underset{j}{\rightarrow}$).($\underset{i}{\rightarrow}$ - $\underset{j}{\rightarrow}$) = $\underset{i}{\rightarrow}^{2}$ - $\underset{j}{\rightarrow}^{2}$ = |$\underset{i}{\rightarrow}$|$^{2}$ - |$\underset{j}{\rightarrow}$|$^{2}$ = 1$^{2}$ - 1$^{2}$ = 0

b) Ta có: $\underset{a}{\rightarrow}$. $\underset{b}{\rightarrow}$ = (2$\underset{i}{\rightarrow}$ + 2$\underset{j}{\rightarrow}$)(3$\underset{i}{\rightarrow}$ - 3$\underset{j}{\rightarrow}$) = 6($\underset{i}{\rightarrow}$ + $\underset{j}{\rightarrow}$)($\underset{i}{\rightarrow}$ - $\underset{j}{\rightarrow}$) = 6. 0 = 0

(a; b) = 90°

Vận dụng 2.

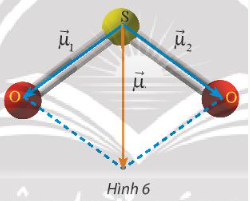
C1: Áp dụng tích vô hướng

($\underset{\mu }{\rightarrow}$)$^{2}$ = ($\underset{\mu _{1}}{\rightarrow}$+$\underset{\mu _{2}}{\rightarrow}$)$^{2}$ = ($\underset{\mu _{1}}{\rightarrow}$)$^{2}$ + ($\underset{\mu _{2}}{\rightarrow}$)$^{2}$ + 2.$\underset{\mu _{1}}{\rightarrow}$.$\underset{\mu _{2}}{\rightarrow}$

= 1,6$^{2}$+1,6$^{2}$+2.1,6,1,6.cos120° 

= 1,6$^{2}$

|$\underset{\mu }{\rightarrow}$|=1,6

C2: Áp dụng hình học phẳng

Hình bình hành SO$_{1}$S'O$_{2}$ có hai cạnh liên tiếp bằng nhau ⇒ SO$_{1}$S'O$_{2}$ là hình thoi.

SO1S' lầ tam giác cân và có một góc bằng 60$^{\circ}$ SO$_{1}$S' lầ tam giác đều.

|$\underset{\mu _{1}}{\rightarrow}$|=|$\underset{\mu _{2}}{\rightarrow}$|=1,6