1. ĐỊNH NGHĨA VECTƠ

Khám phá 1: Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.

Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

• Khối lượng của hàng: 500 tấn.
• Độ dịch chuyển của tàu: 500 km từ A đến B.

Hướng dẫn giải:

Khối lượng là đại lượng chỉ có độ lớn; độ dịch chuyển là đại lượng bao gồm cả độ lớn và hướng.

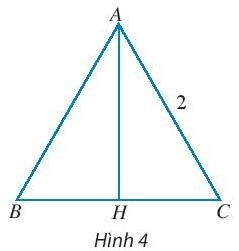
Thực hành 1: Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ $\vec{CH}$, $\vec{CB}$, $\vec{HA}$ trong Ví dụ 1.

Hướng dẫn giải:

• Vectơ $\vec{CH}$ có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.
• Vectơ $\vec{CB}$ có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB.
• Vectơ $\vec{HA}$ có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA.

Ta có: CH = 1; CB = 2 và AH = $\sqrt{3}$ $\Rightarrow$ |$\vec{CH}$| = 1; |$\vec{CB}$| = 2; |$\vec{HA}$| = $\sqrt{3}$

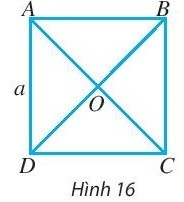
Thực hành 2: Cho hình vuông ABCD có cạnh bằng $\frac{\sqrt{2}}{2}$, hai đường chéo cắt nhau tại O (Hình 5). Tìm độ dài của $\vec{AC}$, $\vec{BD}$, $\vec{OA}$, $\vec{AO}$.

Hướng dẫn giải:

Ta có: AC = BD = $\sqrt{2}$.AD = $\sqrt{2}.\frac{\sqrt{2}}{2}$ = 1;  OA = $\frac{1}{2}$AC = $\frac{1}{2}$

Suy ra: |$\vec{AC}$| = 1, |$\vec{BD}$| = 1, |$\vec{OA}$| = $\frac{1}{2}$, |$\vec{AO}$| = $\frac{1}{2}$

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG

Khám phá 2: Bạn có nhận xét gì về giá của các cặp vectơ $\vec{AB}$ và $\vec{CD}$, $\vec{PQ}$ và $\vec{RS}$ trong Hình 6?

Hướng dẫn giải:

Giá của vectơ $\vec{AB}$ trùng với giá của vectơ $\vec{CD}$, giá của vectơ $\vec{PQ}$ song song với giá của vectơ $\vec{RS}$.

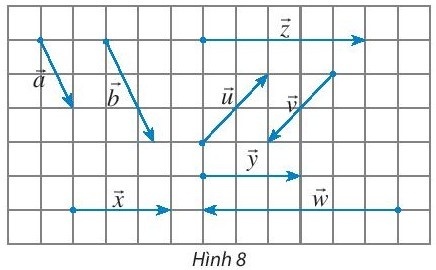
Thực hành 3: Quan sát Hình 8 và gọi tên các vectơ:

a. Cùng phương với vectơ $\vec{x}$;

b. Cùng hướng với vectơ $\vec{a}$;

c. Ngược hướng với vectơ $\vec{u}$.

Hướng dẫn giải:

a. Cùng phương với vectơ $\vec{x}$ là: $\vec{y}$, $\vec{w}$, $\vec{z}$

b. Cùng hướng với vectơ $\vec{a}$ là: $\vec{b}$

c. Ngược hướng với vectơ $\vec{u}$ là: $\vec{v}$

Thực hành 4: Khẳng định sau đây đúng hay sai? Hãy giải thích.

Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ $\vec{AB}$ và $\vec{AC}$ cùng hướng.

Hướng dẫn giải:

Khẳng định sai. Vì đề bài không nêu rõ ba điểm phân biệt A, B, C thẳng hàng theo thứ tự nào, nên nếu A nằm giữa B và C thì hai vectơ $\vec{AB}$ và $\vec{AC}$ ngược hướng.

3. VECTƠ BẰNG NHAU -  VECTƠ ĐỐI NHAU

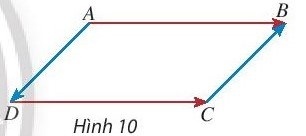
Khám phá 3: Cho hình bình hành ABCD (Hình 10), hãy so sánh độ dài và hướng của hai vectơ:

a. $\vec{AB}$ và $\vec{DC}$

b. $\vec{AD}$ và $\vec{CB}$

Hướng dẫn giải:

a. Hai vectơ $\vec{AB}$ và $\vec{DC}$ cùng hướng và có độ dài bằng nhau.

b. Hai vectơ $\vec{AD}$ và $\vec{CB}$ ngược hướng và có độ dài bằng nhau.

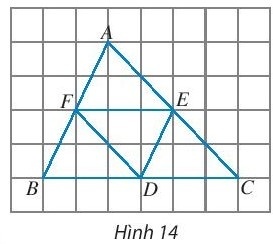
Thực hành 5: Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC (Hình 14).

a. Tìm các vectơ bằng vectơ $\vec{EF}$.

b. Tìm các vectơ đối của vectơ $\vec{EC}$.

Hướng dẫn giải:

a. Các vectơ bằng vectơ $\vec{EF}$ là: $\vec{CD}$, $\vec{DB}$.

b. Các vectơ đối của vectơ $\vec{EC}$ là: $\vec{EA}$, $\vec{CE}$, $\vec{DF}$.

4. VECTƠ-KHÔNG

Thực hành 6: Tìm độ dài của các vectơ $\vec{EF}$, $\vec{EE}$, $\vec{EM}$, $\vec{MM}$, $\vec{FF}$ trong Ví dụ 5.

Hướng dẫn giải:

|$\vec{EF}$| = 2, |$\vec{EE}$| = 0, |$\vec{EM}$| = 1, |$\vec{MM}$| = 0, |$\vec{FF}$| = 0.