CHƯƠNG V. VECTƠ

BÀI 1. KHÁI NIỆM VECTƠ

1. ĐỊNH NGHĨA VECTƠ

HĐKP 1:

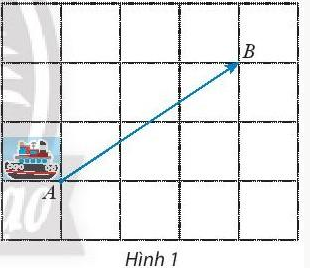
Khối lượng là đại lượng chỉ có độ lớn (500 tấn); độ dịch chuyển là đại lượng bao gồm cả độ lớn (500 km) và hướng (từ A đến B).

Định nghĩa:

Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

- Ví dụ: 

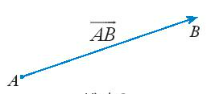
Vectơ có điểm đầu A và điểm cuối B, được kí hiệu: $\underset{AB}{\rightarrow}$.

- Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ $\underset{AB}{\rightarrow}$.

- Độ dài của đoạn thẳng AB gọi là độ dài của vectơ $\underset{AB}{\rightarrow}$ và kí hiệu: |$\underset{AB}{\rightarrow}$|.

Ta có: |$\underset{AB}{\rightarrow}$|=AB.

Chú ý: Một vec tơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là $\underset{a}{\rightarrow}$; $\underset{b}{\rightarrow}$, $\underset{x}{\rightarrow}$, $\underset{y}{\rightarrow}$,...

Ví dụ 1 (SGK - tr82)

Thực hành 1:

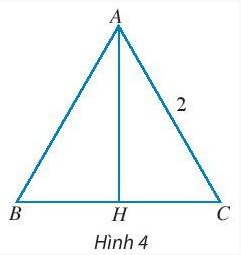
+ Vectơ $\underset{CH}{\rightarrow}$ có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.

+ Vectơ $\underset{CB}{\rightarrow}$ có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB.

+ Vectơ $\underset{HA}{\rightarrow}$ có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA.

Ta có: CH = $\frac{CB}{2}$ = $\frac{2}{2}$ = 1;

AH = $\sqrt{AC^{2}-HC^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$

⟹ |$\underset{CH}{\rightarrow}$| = 1; |$\underset{CB}{\rightarrow}$| = 2; |$\underset{HA}{\rightarrow}$| = $\sqrt{3}$

Thực hành 2:

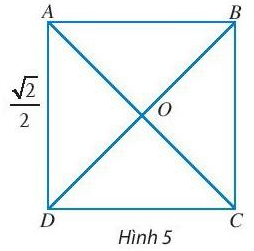
Ta có: AC = BD = $\sqrt{2}$AD = $\sqrt{2}$. $\frac{\sqrt{2}}{2}$ = 1;

OA = $\frac{1}{2}$ AC = $\frac{1}{2}$.1 =$\frac{1}{2}$

Suy ra: |AC| = 1; |BD| = 1; |OA| = $\frac{1}{2}$;

 |AO| = $\frac{1}{2}$.

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG

HĐKP 2:

Giá của vectơ $\underset{AB}{\rightarrow}$ là đường thẳng AB, giá của vectơ $\underset{CD}{\rightarrow}$ là đường thẳng CD. 

⟹ Giá của vectơ $\underset{AB}{\rightarrow}$ trùng với giá của vectơ $\underset{CD}{\rightarrow}$.

Tương tự, giá của vectơ $\underset{PQ}{\rightarrow}$ song song với giá của vectơ $\underset{RS}{\rightarrow}$.

Kết luận:

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét: Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

Ví dụ 3 (SGK - tr83)

Thực hành 3: 

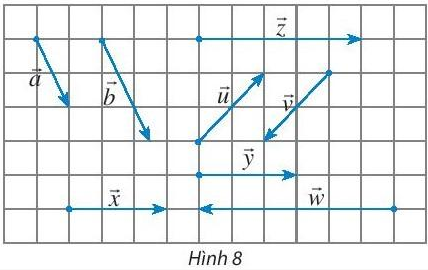
a) Cùng phương với vectơ $\underset{x}{\rightarrow}$ là: $\underset{y}{\rightarrow}$; $\underset{w}{\rightarrow}$; $\underset{z}{\rightarrow}$.

b) Cùng hướng với vectơ $\underset{a}{\rightarrow}$ là: $\underset{b}{\rightarrow}$.

c) Ngược hướng với vectơ $\underset{u}{\rightarrow}$ là: $\underset{v}{\rightarrow}$.

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ cùng phương.

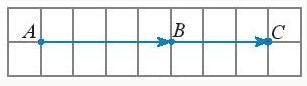
Thực hành 4:

Khẳng định sai. Vì đề bài không nêu rõ ba điểm phân biệt A, B, C thẳng hàng theo thứ tự nào, nên nếu A nằm giữa B và C thì hai vectơ $\underset{AB}{\rightarrow}$ và $\underset{AC}{\rightarrow}$ ngược hướng.

3. VECTƠ BẰNG NHAU – VECTƠ ĐỐI NHAU 

HĐKP 3:

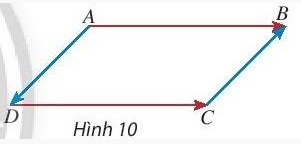
a) Hai vec tơ $\underset{AB}{\rightarrow}$ và $\underset{DC}{\rightarrow}$ cùng hướng và có độ dài bằng nhau.

b) Hai vec tơ $\underset{AD}{\rightarrow}$ và $\underset{CB}{\rightarrow}$ ngược hướng và có độ dài bằng nhau.

Kết luận:

Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ được gọi là bằng nhau nếu chúng có cùng hướng và có cùng độ dài, kí hiệu là $\underset{a}{\rightarrow}$ = $\underset{b}{\rightarrow}$.

Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu $\underset{a}{\rightarrow}$ = -$\underset{b}{\rightarrow}$. Khi đó, vectơ $\underset{b}{\rightarrow}$ được gọi là vectơ đối của vectơ $\underset{a}{\rightarrow}$.

Chú ý:

a) Cho vectơ $\underset{a}{\rightarrow}$ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho $\underset{OA}{\rightarrow}$ = $\underset{a}{\rightarrow}$. Khi đó, độ dài của vectơ $\underset{a}{\rightarrow}$ là độ dài đoạn OA, kí hiệu là |$\underset{a}{\rightarrow}$|.

b) Cho đoạn thẳng MN, ta luôn có $\underset{NM}{\rightarrow}$ = - $\underset{MN}{\rightarrow}$.

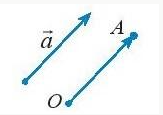
Ví dụ 4 (SGK - tr85)

Thực hành 5:

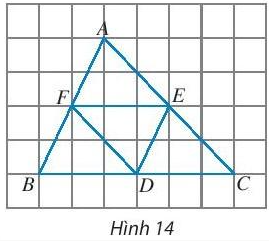
a) Các vectơ bằng vectơ $\underset{EF}{\rightarrow}$ là: $\underset{CD}{\rightarrow}$; $\underset{DB}{\rightarrow}$

b) Các vectơ đối của vectơ $\underset{EC}{\rightarrow}$ là $\underset{EA}{\rightarrow}$; $\underset{CF}{\rightarrow}$;$\underset{CE}{\rightarrow}$

4. VECTƠ-KHÔNG 

Khái niệm:

Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là $\underset{0}{\rightarrow}$.

Chú ý:

+ Quy ước vectơ-không có độ dài bằng 0.

+ Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.

+ Mọi vectơ-không đều bằng nhau $\underset{0}{\rightarrow}$ = $\underset{AA}{\rightarrow}$ = $\underset{BB}{\rightarrow}$=$\underset{CC}{\rightarrow}$ = ... với mọi điểm A, B, C,...

+ Vectơ đối của vectơ-không là chính nó.

Ví dụ 5 (SGK - tr86)

Thực hành 6:

$\underset{EE}{\rightarrow}$;$\underset{MM}{\rightarrow}$;$\underset{FF}{\rightarrow}$ có điểm đầu và điểm cuối trùng nhau nên chúng là vec tơ-không, có độ dài bằng 0.

|$\underset{EE}{\rightarrow}$| = |$\underset{MM}{\rightarrow}$| = |$\underset{FF}{\rightarrow}$| = 0

$\underset{EF}{\rightarrow}$= 2; $\underset{EM}{\rightarrow}$ = $\frac{1}{2} \underset{EF}{\rightarrow}$ = 1 ⟹ |$\underset{EF}{\rightarrow}$| = 2;

|$\underset{EM}{\rightarrow}$| = 1